차세대 반도체 소자용 세라믹 박막의 전기적 분석 방법 리뷰
Review of Electrical Characterization of Ceramic Thin Films for the Next Generation Semiconductor Devices
Article information
Abstract
Abstracts
Ceramic thin films are key materials for fundamental electronic devices such as transistors and capacitors which are highly important for the state-of-the-art electronic products. Their characteristic dielectric properties enable accurate control of current conduction through channel of transistors and stored charges in capacitor electrodes. The electronic conduction in ceramic thin films is one of the most important part to understand the electrical properties of electronic device based on ceramic thin films. There have been numerous papers dealing with the electronic conduction mechanisms in emerging ceramic thin films for future electronic devices, but these studies have been rarely reviewed. Another interesting electrical characterization technique is one based on electrical pulses and following transient responses, which can be used to examine physical and chemical changes in ceramic thin films. In this review, studies on various conduction mechanisms through ceramic thin films and electrical characterization based on electric pulses are comprehensively reviewed.
1. 서론
4차 산업혁명과 함께 현대사회의 정보의 양은 기하급 수적으로 증가하고 있고,이러한 방대한 양의 정보를 저 장하고 처리하기 위한 반도체 소자의 수요 또한 꾸준히 증가하고 있다.[1] 반도체 소자 등을 기반으로 한 다양한 종류의 전자기기에는 세라믹 박막이 필수적인 소재로 포 함되고 있다. 예를 들어,스위치 역할을 하는 기본 소자 라 할 수 있는 트랜지스터에는 게이트 절연막의 자리에 산화하프늄 박막이 활용되고 있으며,Dynamic Random Access Memory (DRAM)의 셀 캐패시터에서는 유전막 으로 현재 산화지르코늄/산화알루미늄/산화지르코늄의 3중층 구조가 활용되고 있는 상황이다.[1,2] 이와 같은 핵 심 소재들은사물인터넷 기반전자기기들,클라우드서 비 스룰 위한 데이터센터,스마트 운송기기,빅데이터 등의 4차 산업혁명의 여러 핵심 기술들과 필연적으로 밀접하 게 연관된다. 즉,4차 산업혁명의 핵심 기술들의 발전을 위해서는 반도체 소자들의 성능 향상이 높은 중요성을 가 지게 되며,이 때문에 반도체 소자용 산화물 박막에 대한 연구 또한 매우 중요하다. 전자 소자 내에서 세라믹 박막 이 캐패시터,트랜지스터 등의 기본 소자의 성능을 좌우 하게 되기 때문에 세라믹 박막의 전기적 특성을분석하는 일은 전자 소자의 성능을 평가하고 향상시키기 위해 필수 적이다. 따라서,본 논문에서는 차세대 반도체 소자용 세 라믹 박막의 전기적 특성을 분석하는 연구의 최신 동향을 살펴보고자 한다.
2. 전류암 특성 기반 전도 매기니즘 분석
게이트 절연막이나 캐패시터의 유전층으로 삽입된 세 라믹 박막의 경우에 동작전압에서 낮은 누설전류 밀도를 가지며 충분한 유전율을 기반으로 필름표면에 표면전하 를 유도하는 것이 핵심적인 역할이다. 따라서,직류전압 하에서 누설전류 특성을 분석하는 것이 절연막으로서의 성능을 평가하기 위한 핵심적인 분석방법이 되게 된다. 전류-전압 특성 분석을 통해서 단순히 각 전압하에서의 전류값을 측정할 수 있을 뿐만 아니라,전하 캐리어의 conduction mechanism을 분석하는 데에도 활용하는 것이 가능하다. 본장에서는캐리어의 다양한 conduction mechanism을 분석하는 방법에 대해서 종합적으로 기술 하고자 한다.
전류-전압 특성의 분석을 위한 전기회로는 상대적으 로 매우 간단한 형태를 가지고 있다. Voltage source,캐 패시터,Ammeter가 직렬로 연결되어 있는 회로를 사용 해 간단히 평가하는 것이 가능하며,반도체 소자의 경우 이와 같은 측정을 위해 Semiconductor Parameter Analyzer라 부르는 계측장비와 전기적인 contact을 위 한 2개의 프로브를 포함한 프로브스테이션을 주로 이용 하게 된다. 특히,전류-전압의 상관 관계로부터 유추된 전도 메커니즘이 정확한 것인지 판단하기 위해서는 많은 경우에 전류-전압 특성의 온도 의존성을 관찰하는 것이 필수적이다. 따라서,전도 메커니즘 분석을 위해서는 프 로브스테이션의 샘플 스테이지의 온도를 바꿀 수 있는 hot chuck,혹은 진공 분위기에서 온도를 낮출 수 있는 챔버가 추가적으로 필요하다. 캐패시터 소자의 경우에는 프로브와 전기적인 컨택을 하기 위해서 충분히 낮은 저항 을 가지는 전도성 전극물질을 이용하며,일반적으로 금 속-유전체-금속,혹은 금속-유전체-반도체와 같은 형 태의 소자를 제작하여 평가한다. 전도 메커니즘 분석을 위해서는 우선 다양한 전도 메커니즘에 대한 전류-전압 의 관계식을 이해하고 있어야 하며,자세한 이론적인 부 분은 아래에서 다루기로 한다.
Conduction mechanism은 크게 interface—limited conduction mechanism과 bulk-limited conduction mechanism으로 나뉘다. 전자는 유전막과 금속 전극의 계면에 의해서 carrier의 conduction이 제한되는 메커니 즘으로 Schottky emission (or thermionic emission), Fowler-Nordheim tunneling, Direct tunneling, Thermionic field emission 등의 mechanism이 여기에 포함된다. 후자는 금속/유전막 계면이 아닌 유전막의 bulk 영역에 의해서 conduction이 제한되는 메커니즘을 통틀어 가리키며,Poole—Frenkel emission,Hopping conduction, Ohmic conduction, Space-charge-limited conduction (SCLC) 등이 포함된다. 2.1.1— 2.1.2 장에서 각각의 conduction mechanism을 자세히 살펴보기로 한다.
2.1. Interface limited conduction
2.1.1. Schottky emission
Schottky emission 혹은 thermionic emission은 그림 1에서 볼 수 있듯이 carrier가 금속 전극과 유전막의 계면에서 형성된 Schottky barrier를 thermal energy 로 극복하면서 나타나는 conduction이다. 계면에서의 energy barrier 극복에 의해서 conduction rate가 좌우 되기 때문에 계면에 존재하는 trap site 등의 무시되는 이상적인 경우에 금속의 workfunction과 유전막의 electron affinity의 차이에 의해서 barrier 높이가 결정 된다. 이 때 나타나는 current density는 식 1과 같이 나타낼 수 있다.
식 1에서 A*는 effective Richardson constant,m0는 자유 전자의 질량,m*는 유전막에서의 유효전자질량,T 는 절대온도,Φβ는 Schottky barrier height (또는 conduction band offset), 표는 유전막에 걸리는 전계,k 는 볼츠만 상수,느는 플랑크 상수,ε。는 진공의 유전율,ερ 은 유전막의 유전상수에 해당한다. 한가지 유의할 점은 유전상수 ερ은 전기적으로 측정되는 electrical dielectric constant가 아니라 optical dielectric constant (or dynamic dielectric constant)로 일반적으로 유전막의 굴절율의 제곱과 유사한 값을 가진다는 점이다. 일반적으 로 optical dielectric constant는 electrical dielectric constant 보다 훨씬 작은 값을 가진다.
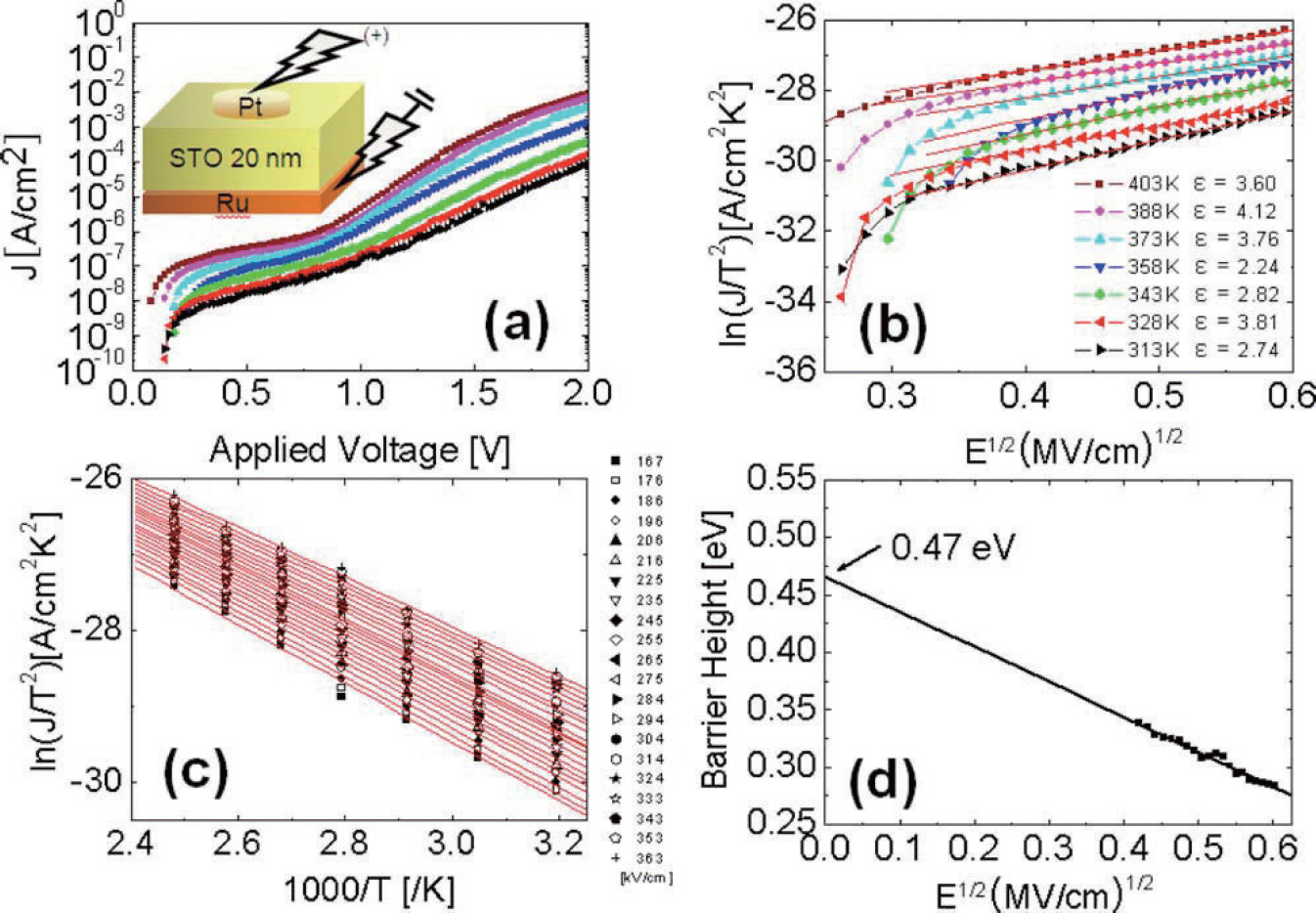
그림 2는 차세대 초고유전율 유전막으로 큰 관심을 받고 있는 SrTiO3라는 폐로브스카이트 구조 산화물을 포함한 Pt/SrTiO3/Ru의 metal-insulator-met율ᅵ 구조의 캐패시 터에서 conduction mechanism 분석을 통해 Schottky emission을확인한실험결과로 Lee 등에의해서보고되 었다.[3] 우선 실험을 통해서 얻는 raw data는 그림 2a 에서 볼 수 있듯이 다양한 온도에서 측정한 전류밀도-전 압 곡선이다. 식 1을 변형시키면 ln(J/T2)은 온도가 일정 할 때에 E1/2에 비례하는 특성이 있다. 따라서,그림 2b에 서볼수있듯01 각온도에서곡선/T2) 과1수2을 plot 하여 선형적 비례 관계가 나타나는 구간을 찾아야 한다. 그러 한 전계 구간을 찾을 수 있다면,그 구간은 Schottky emission이 실제로 나타날 수 있는 구간에 해당된다. 하 지만,이선형적관계가실제로 Schottky emission 임을 증명하는 충분 조건이 되지는 못한다. 정확한 검증을 위 해서는 전류밀도와 온도의 관계를 추가적으로 확인해야 한다.
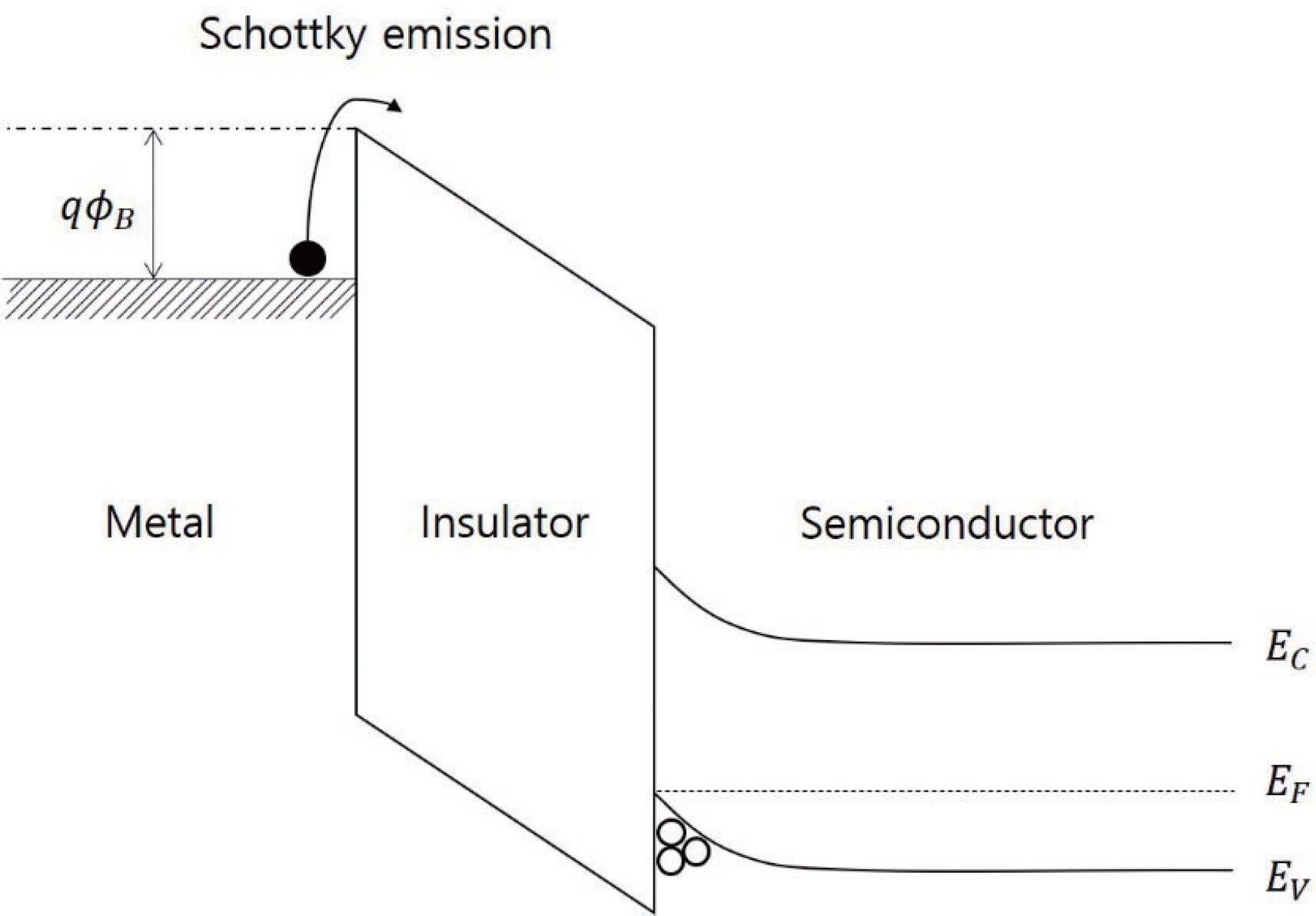
Metal-insulator-semiconductor stack에서 metal쪽에서 전 자가 injection되어 Schottky emission이 나타날 때의 electric band 모식도
식 1에 따르면 ln(J/T2)은전계가 일정한상황에세/T 에 선형적으로 비례하는 관겨 임을 알 수 있다. 따라서,다 양한 온도에서 측정한 전류밀도-전압 특성에서 여러 온 도의 같은 전계값에서 측정된 전류밀도 값들을 묶어서 그 래프를 그려 그 관계를 확인하는 단계가 필요하다. 그림 2c는이러한목적으로 ln(J/T2)과 1000/T를 plot 한결과 를 보여준다. 실제로 선형적인 관계가 나타나는 것을 그 림 2c에서 확인 가능하다. 그림 2b와 2c 에서전계의존성 과 온도의존성에서 실제 Schottky emission을 따르는 conduction이 관찰됨을 확인하였지만,최종적인 검종 위해서는 마지막 단계로 유전상수 값이 실제 유전막의 optical constant 값과 일치하는지 확인이 필요하다.
이는 그림 2c의 그래프의 기울기 값
식 1 에서 전계 Ε가 걸려 있을 때의 effective barrier height
2.1.2. Fowler-Nordheim tunneling
Schottky emission이 carrier들이 thermal energy 에 의해서 energy barrier를 극복하고 주입되는 것에 의 해 나타나는 반면에 Fowler-Nordheim tunneling은 thermal energy둘이 없이 energy barrier를 tunneling으로 통과하여 생기는 면한양자역학적인현상이다. 그림 3 에서 볼 수 있듯이 F-N tunneling은 유전막에 높은 전 계가 가해져 barrier의 폭이 유전막의 두께보다 더 얇아 질 때,tunneling에 의해 carrier가 통과할 확률이 높아 지면서 나타난다. 이러한 점이 다음 장에서 소개되는 direct tunneling개되의 차·이점이이. Direct tunneling의 경우에는 F-N tunneling보다 비교적 낮은 전계에서 나 타나며,potential barrier의 폭이 1 더 작아지는 효과가 없 는 상황에서 관찰되는 tunneling에 의한 conduction이 다. F-N tunneling에 의한 전류밀도는 다음 식 2에 의 해서 설명된다.
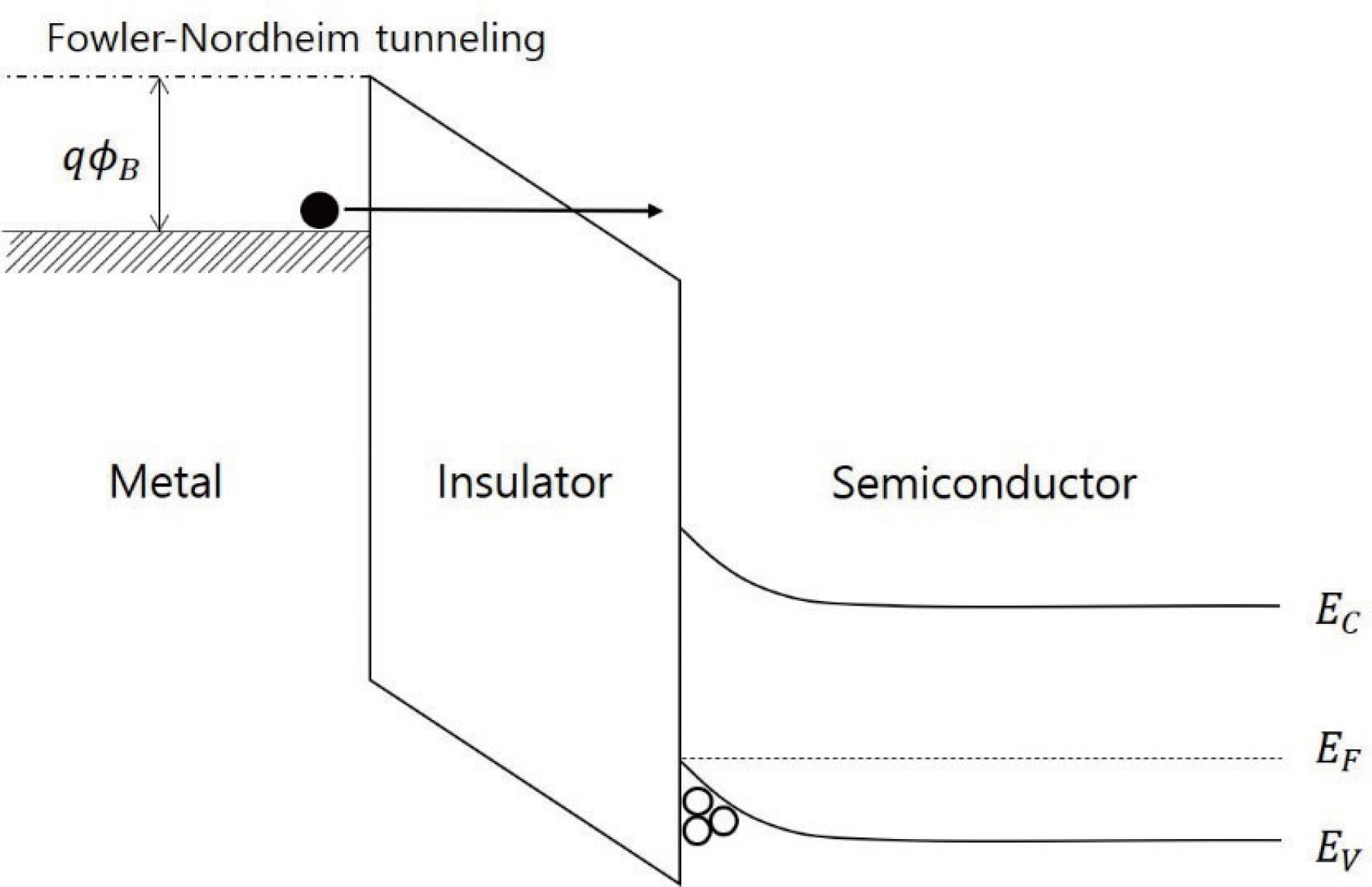
Metal-insulator-semiconductor stack에서 metal쪽에서 전 자가 injection되어 Fowler-Nordheim tunneling이 나타날 때 의 electric band 모식도
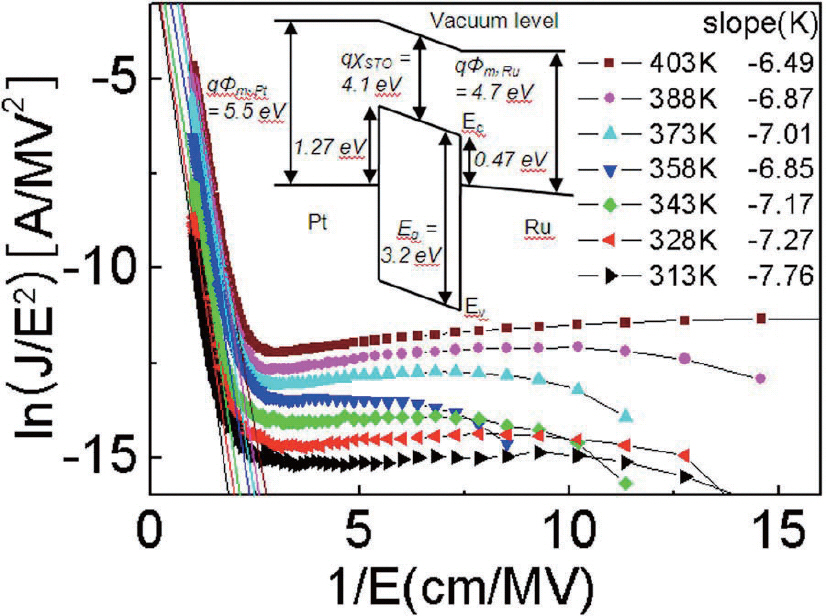
식 2로부터 F-N tunneling을 따르는 conduction은 ln(J/E2)을 1/E의 함수로 plot하였을 때에 선형적인 관계 가 나타남을 알 수 있다. 그림 4는 2.1.1.1장에서 인용된 Lee 등의 연구결과의 전류밀도-전압 측정 결과를 F-N tunneling mechanism 적용을 위하여 ln(J/E2)-1/E의 관계를 plot한 것이다. 그림 4에서 볼 수 있듯이 다양한 온도에서 측정된결 3측!이 모두 0.3 MV/cm 이상의 높 은 전계영역에서 linear한 관계가뚜렷이 관찰되는 것을 확인할 수 있다. 이러한 결과는 관찰된 결과가 F-N tunneling에 따른 conduction mechanism을 따를 확률 이 존재함을 암시한다.
실제 이 mechanism이 적용되는지를 검증하기 위해서 는 주71″적으로 electron의 tunneling effective mass 값 을 계산해볼 필요가 있다. 그림 4에서 선형관계가 나타나 는 높은 전계 영역에서의 slope를 구하면,각온도에서의
그림 2와 그림 4로부터 얻을 수 있는 또 다른 교훈은 같 은 소자라 하더라도 전계 영역에 따라서 지배적인 conduction mechanism이 변할 수 있다는 것이다. Lee 등의 연구에서의 결과는 전계가 낮게 걸린 상태에서는 Schottky emission에 따르는 즉,열에너지에 의하여 potential barrier를 극복하여 나타나는 mechanism이 지배적인 반면에 높은 전계에서는유전막의 band의 변형 이 일어나며 barrier 유효한 폭이 짧아지는 효과가 나타 나며,F-N tunneling이라는 양자역학적 효과가 지배적 으로 나타나는 것으로 변한다는 것이다.[3] 또한, conduction mechanism은 온도에 의해서도 큰 영향을 받게 된다. 예를 들어 고온에서는 열에너지를 기반으로 한 Schottky emission 등의 지배적인 conduction mechanism이었던 소자가 저온에서는 열에너지가 필요 하지 않은 F-N tunneling 등의 mechanism에 의한 conduction을 보이는 식으로 바뀔 수 있다. 실제로, F-N tunneling은 열에너지를 필요로 하지 않는동작메 커니즘 때문에 상대적으로 저온에서 더 뚜렷이 관찰될 때 가 많은 것으로 알려져 있다.[4]
2.1.3. Direct tunneling
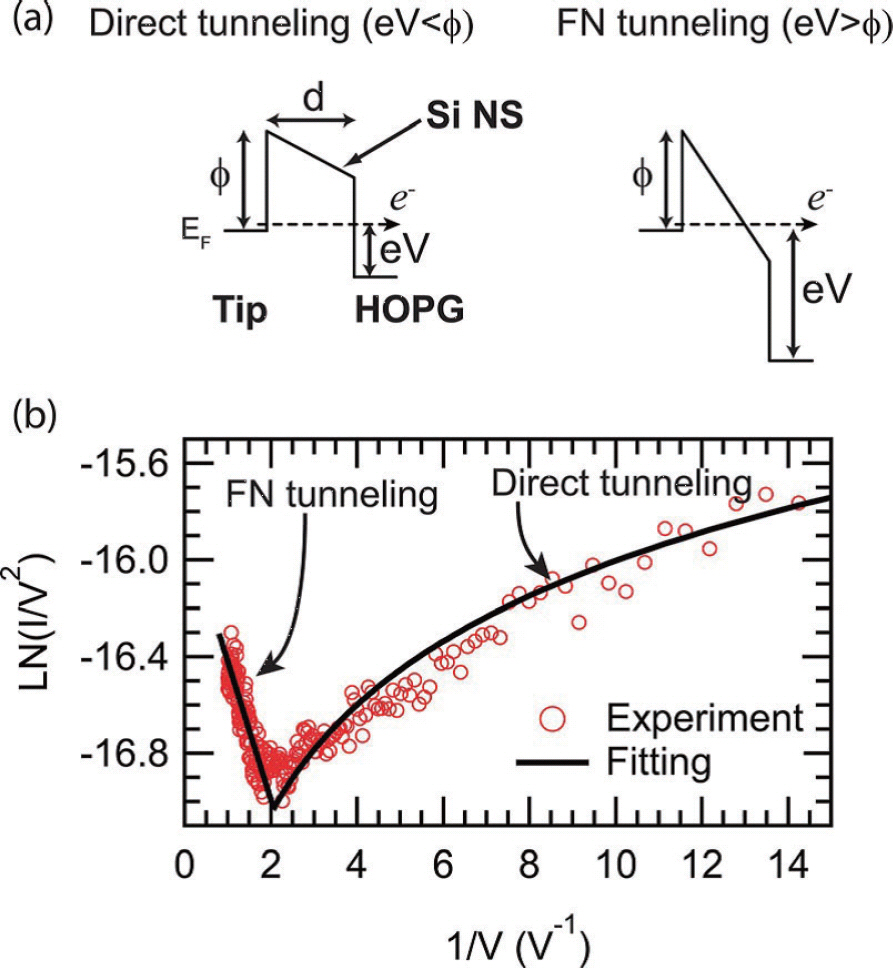
Direct tunneling은 F-N tunneling과 비슷하게 유한 한 높이와 폭을 가지는 potential energy barrier룰 electron wave function이 투과하여 지나갈 확률이 유 한하다는 양자역학적인 메커니즘 이다. F-N tunneling 과의 차이는 F-N tunneling의 경우에는 유전막의 높은 전계에 의해서 electron wave function이 통과해야 하 는 energy barrier의 두께가 실제 유전막보다 얇아지는 경우이나(그림 3) direct tunneling의 경우는 상대적으 로 F-N tunneling보다 낮은 전계에서 유전막의 두께와 같은 potential energy barrier를 통과해야 한다는 점이 다.(그림 5) 이 두 mechanism의 차이는 그림 6의 a와 b 에서도 확인할수 있다. 그림에서 확인할수 있듯이 F-N tunneling와 direct tunneling의 mechanism의 전환이 확인되는 조건은 유전막에 걸리는 전압 V가 barrier의 높 이가 Φρ일 때이다. V〉>Φβ일 때에는 electron wave function이 투과해야하는 barrier폭。1 유전막 두께보다 얇아지면서 F-N tunneling이 관찰되며,V<fp 일 때에는 electron wave function이 투과하는 barrier의 폭이 유 전막 두께와 같다. 따라서,전계의 측면에서는 F-N tunneling 보다상대적으로낮은전계가걸려있는상황 에서 관찰되며,온도 측면에서는 열에너지에 의한 thermionic emission등의 메커니즘에 의한 conduction ᄋ 더 적게 나타나는 저온 조건에서 관찰될 확률이 높다. Direct tunneling에의한conduction은식 3에 의해서 표현된다.
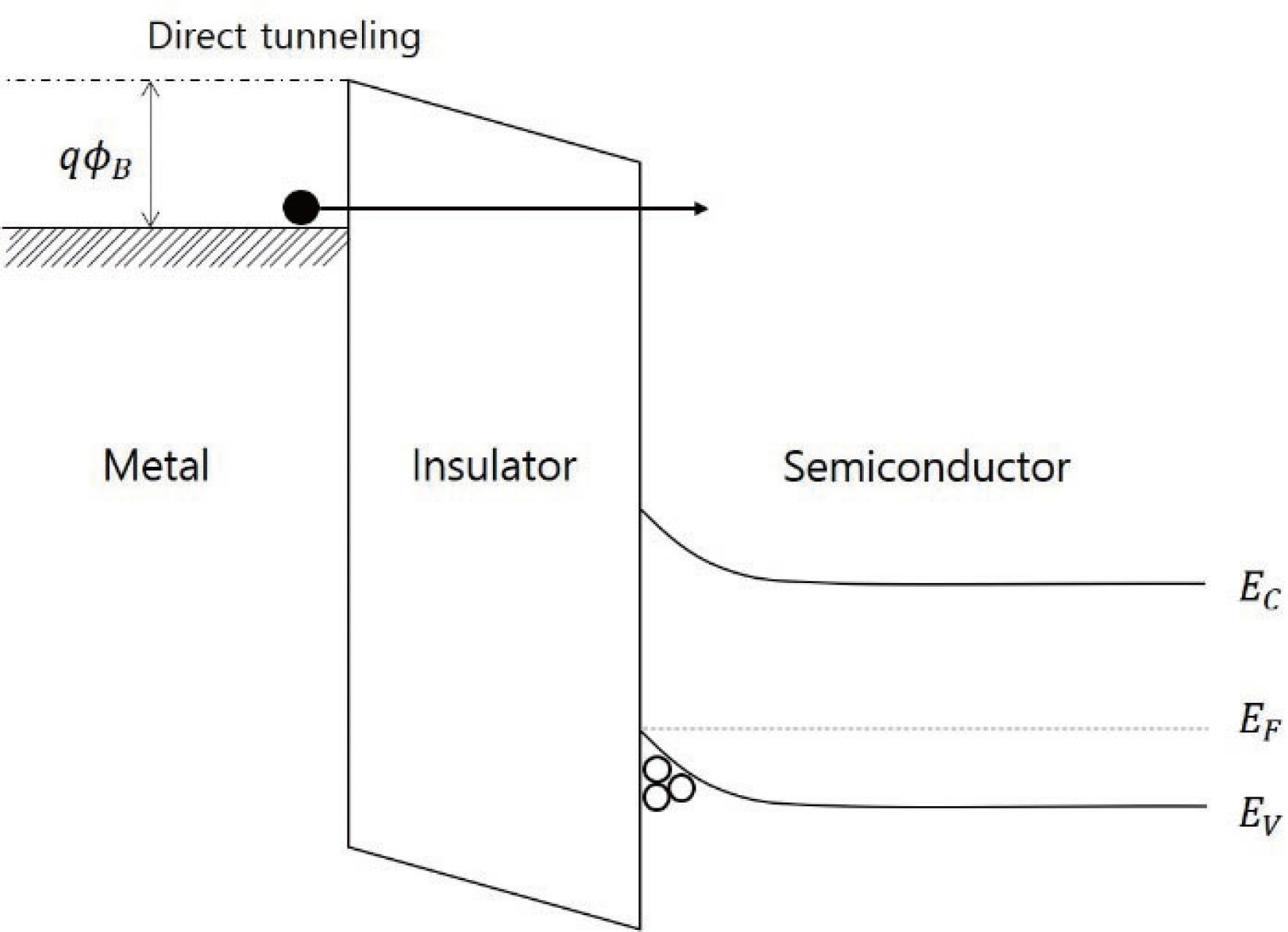
Metal-insulator-semiconductor stack에서 metal쪽에서 전 자가 injection되어 direct tunneling이 나타날 때의 electric band 모식도
Ikuno 등이 보고한 highly oriented pyrolytic graphite (HOPG)상에 형성된 Si nanosheet을 통한 tunneling current를 conductive atomic force microscopy (CAFM) 를 이용하여 분석한 결과가그림 6에 요약되어 있다.[5] 즉, 측정과정에서는 CAFM cantilever/Si nanosheet/HOPG stack의 캐패시터 구조의 conduction이 분석되었다볼 수 있다. 그림 6c에서 볼 수 있듯이 ln(I/V2)을 1/V의 함수로 plot하였을 때 뚜렷하게 2개의 영역으로 나누어지는 것을 볼수 있다. 높은 전계 영역에서는 F-N tunneling이 관찰 되는데,이 영역에서는 ln/V2)이 −(1/V)에 비례하는관계 가 있다. 이는 식 2에서도 뚜렷이 확인이 하다. 반면에 상대적으로낮은 전계 영역에서는 lnI/V2)이 ln/V)에 비 례하는 관계가 확인된다. 이러한 관례를 바탕으로 fitting 을 진행한 결과 (그림 6c의 흑색 곡선)이 실험값 (red open circle)과 잘 맞는 결과를 확인할 수 있다.
2.1.4. Thermionic-field emission
Thermionic-field emission은 thermionic emission 과 field emission의 중간 특성을 보인다. 그림 7이 thermionic emission, field emission, thermionic field emission을 비교하여 보여준다. Field emission은 F-N tunneling이나 direct tunneling과같이 열에너지의 관여 없이 순수하게 field에 의해서 일어나는 conduction을 칭 한다. 반면에 thermionic emission을 thermal energy에 의해서 energy barrier룰 극복하고 나타나는 conduction 이다. Thermionic-field emission은 열에너지에 의하여 전자의에너지준위가 높아지되완전히 barrier를열에너 지에 의해 극복하는 것이 아니라 더 높은준위에서 얇아진 barrier를 tunneling mechanism으로 지나가는 현상으 로 볼 수 있다. Thermionic-field emission에 의한 current density는 식 4에 의해서 표현되며,식 4에서 사 용된 기호들은 앞에서 정의된 것과 같다ᅳ.
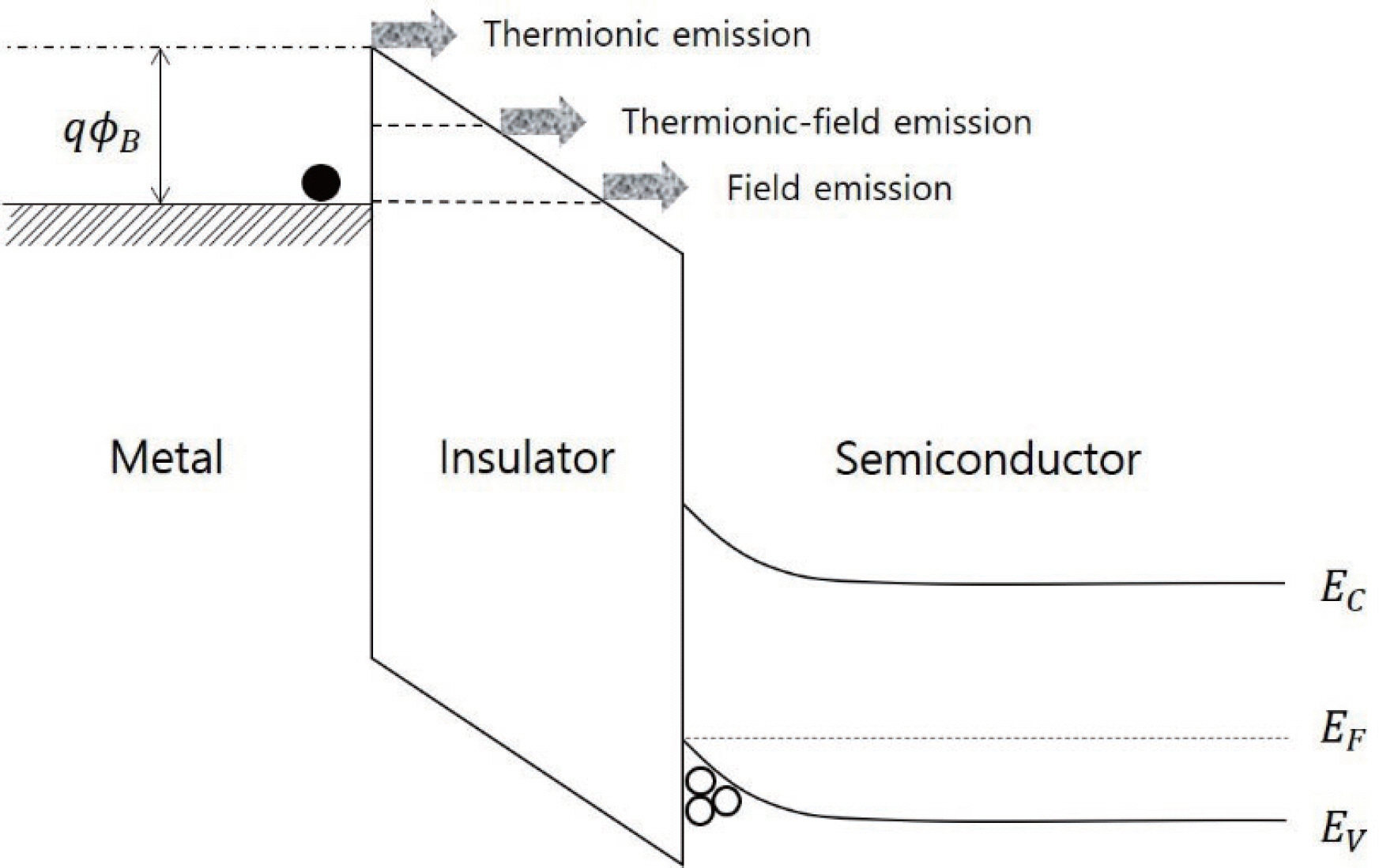
Metal-insulator-semiconductor stack에서 metal쪽에서 전 자가 injection되어 thermionic emission, thermionic-field emission, field emission이 나타날 때를 비교한 electric band 모식도
2.2. Bulk limited conduction
2.2.1. Poole-Frenkel conduction
Bulk-limited conduction 의경우에 interface-limited conduction과 다르게 전자가 계면에서 주입되 는 메커니즘이 아니라유전막 내에서의 conduction에 의 해서 current density가결정되는경우에 해당된다ᅳ이 때문에 bulk-limited conduction mechanism이 관찰 되는 소자에서는 mechanism 분석을 통해서 유전막 내 에 있는 trap energy level,trap density,trap spacing, electronic drift mobility,dielectric relaxation time 등의 다양한 유전막 특성을 추출하는 것이 가표하다.[4]
Poole-Frenkel emission (P-F emission)은 bulk-limited mechanism이라는 점에서는 Schottky emission 과 근본적으로 다르나 전자의 conduction이 열적으로 excite되어 energy barrier를 극복하면서 나타난다는 점 에서는 유사점을 가진다. 그림 8에서 볼 수 있듯이 전자가 유전막 내에 있는 trap site들을 통해서 conduction이 나 타나며,trap site 사이의 이동은 energy barrier를 열적 으로 excite된 전자가 극복하면서 하게 된다. P-F emission의전류밀도는식 5에의해서표현된다.
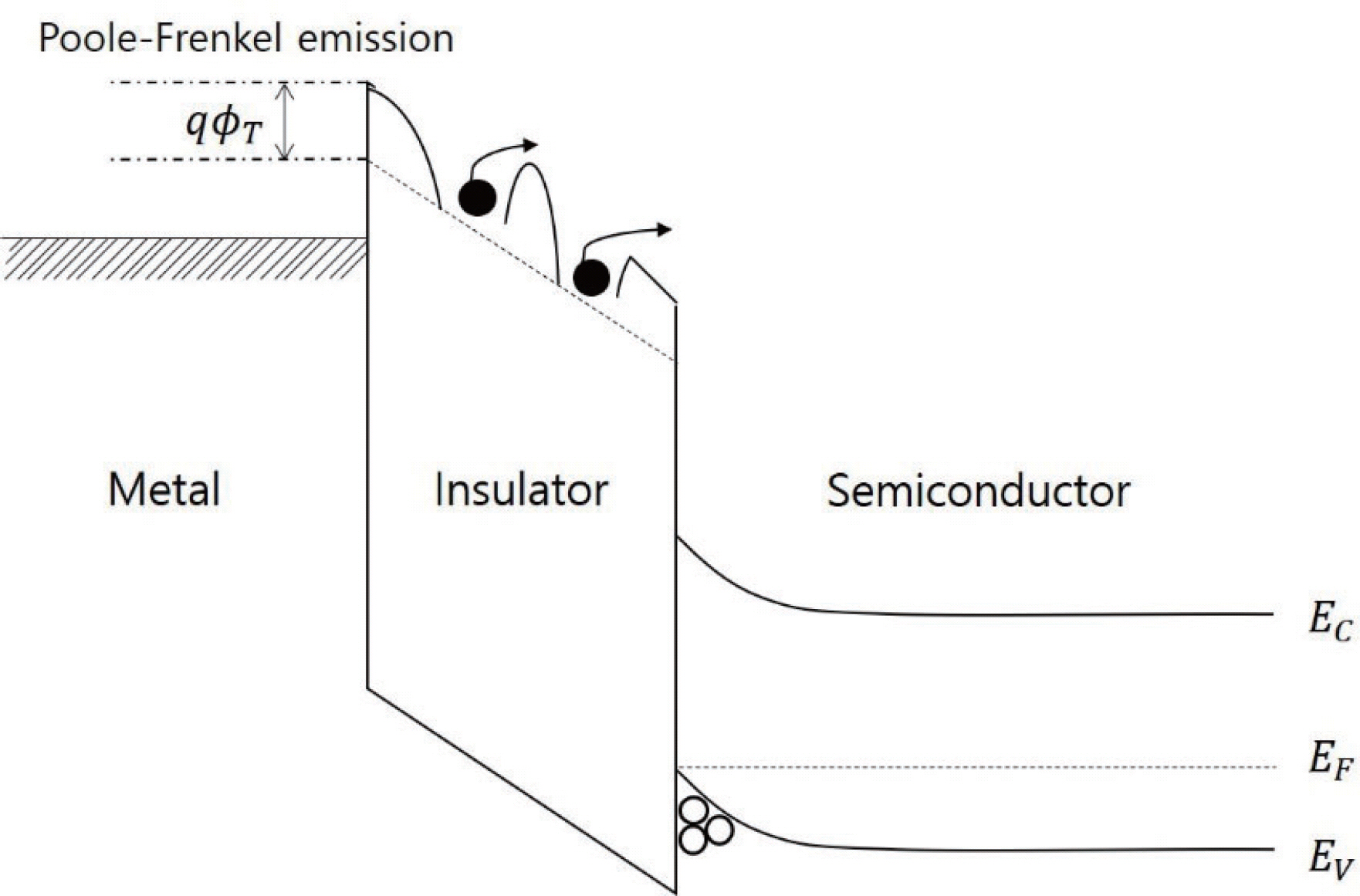
Metal-insulator-semiconductor stack에서 metal쪽에서 전 자가 injection되어 Poole-Frenkel emission이 나타날 때의 electric band 모식도
식 5에서 μ은 electron drift mobility, Nc는 conduction band의 density of states, 는 trap energy level이며 나머지 기호는 앞에서 정의되었던 것 과 같다. 이 중 Nc는 乂 =3D 2[관3/2으로 일반적으로 표현 되며 t3/2에 비례하는 특성을 가진다. Thermionic emission의 식과 비교했을 때,Schottky barrier term 이 exponential 함수에 들어가 있는 것과 달리 P-F emission에는 trap energy level이 포함되어 있는 것을 볼 수 있다. 이는 그림 7에서 볼 수 있듯이 열적으로 excite된 전자가 trap 사이의 energy barrier를 극복하 며 나타나는 메커니즘 때문이다.
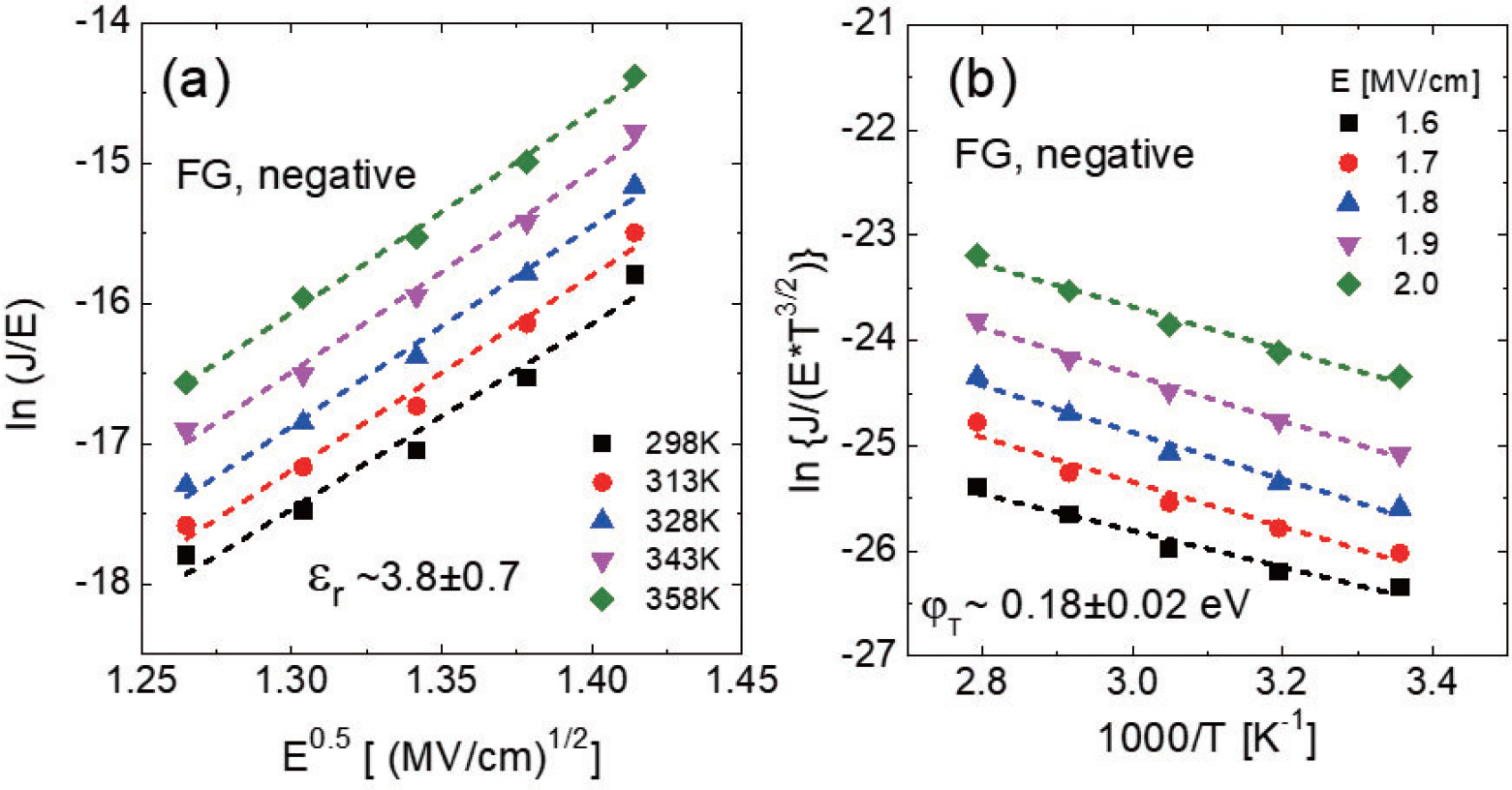
Park 등은[6] 2016년에 차세대 강유전체로 큰 관심을 얻고 있는 Hf0.5Zr0.5O2 (HZO)를 유전막으로 人않한 Pt/ TiN/HZO/TiN stack의 캐패시터를 제작하고 그 conduction mechanism을 분석하였다. 이 때에 약 1.5 – 2.2 MV/cm의 전계 영역에서 P-F conduction으로 보이는구간이 존재함을확인하였다. 다양한 온도에서 측 정된 data를 분석한 결과 해당 전계 구간에세n(J/E)를 E1/2의 함수로 plot하였을 때에 선형적인 관계가 나오는 것이 그림 9a에서 볼 수 있듯이 확인되었다. 그림 8a의 각 온도에서의 그래프의 기울기는
2.2.2. Hopping conduction
Hopping conduction은 P-F emission과 유사하게 유전막내에존재하는trap들을통해서 전자의 이동이 일 어나게 되지만,P-F emission이 trap간의 이동의 thermally activated process로 일어나는 반면에 Hopping conduction에서는 tunneling에 의해서 trap 사이의 이동이 나타나게 된다. (그림 10) Hopping conduction에 의한 전류밀도는 식 6에 의해서 나타낼 수 있다.
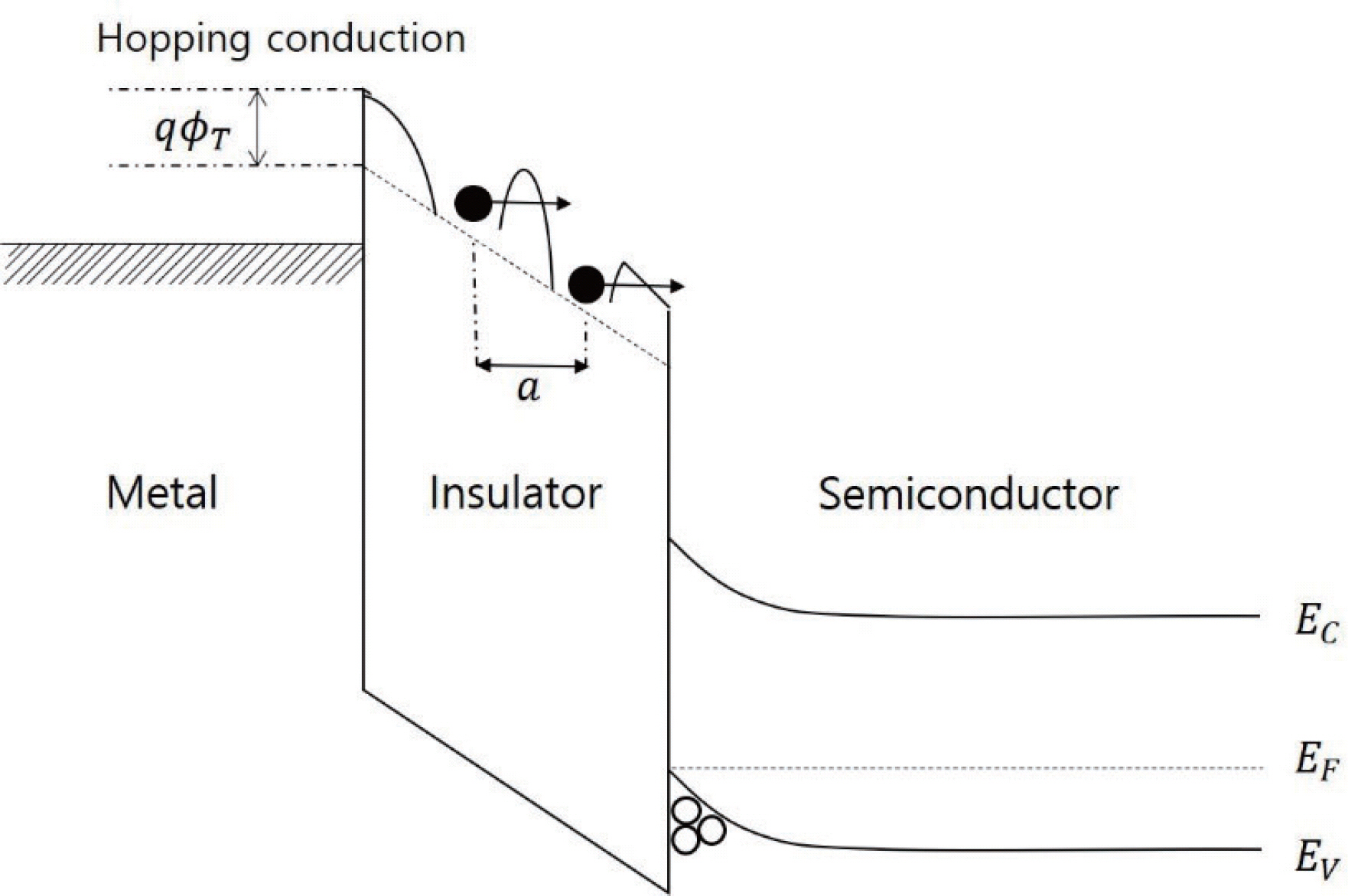
Metal-insulator-semiconductor stack에서 metal쪽에서 전자가 injection되어 Hopping conduction이 나타날 때의 electric band 모식도.
식 6에서 a는 평균적인 hopping distance,즉 trap 사이 의 평균거리에 해당하며,n은 유전막conduction band의 전자 밀도에 해당하고,ν는 trap site에서 전자의 vibration frequency에 해당한다. Ea는 activation energy로 trap state부터 conduction band의 바닥까지의 에너지차에 해 당한다. 다른 term들의 앞에서 정의했던 것과 같다.
2.2.3. Ohmic conduction
Ohmic conduction은 conduction band의 전자나 valence band의 hole의 drift에 의해서 나타나는 conduction mechanism이다. ᄋhmic conduction에 의 해서나타나는전류밀도는식7에의해서기술될수있으 며,식 7에서 볼 수 있듯이 전류밀도와 전계는 선형적인 비례관계를 가진다. 이와 같은 conduction은 Schottky emission과 다르게 유전막의 electron affinity가 금속 전극의 일함수보다 더 커서 φβ 가 존재하지 않거나,φβ 가 매우 작은 상황에서 관찰될 수 있다.
식 7에서 σ는 conductivity를 의미하며,나머지 term 의 정의는 앞과 같다.
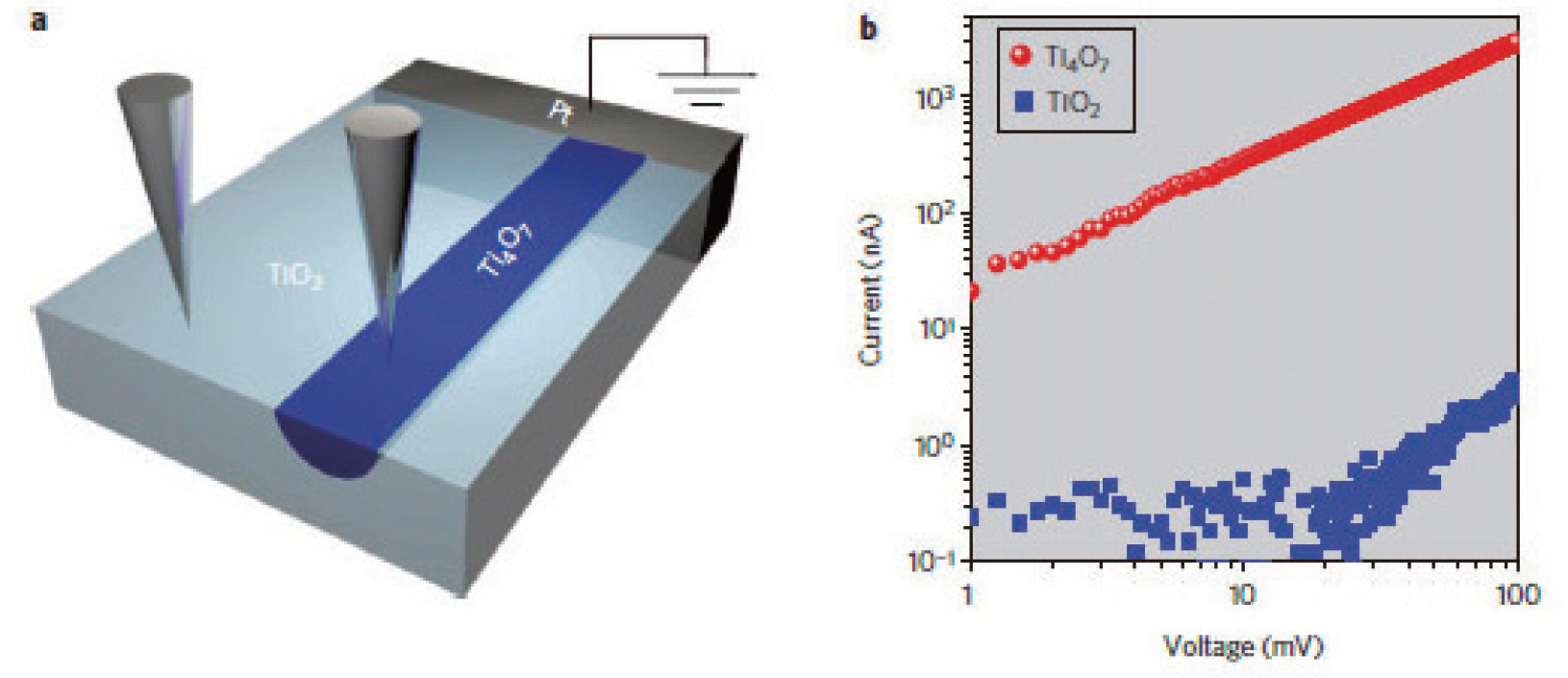
Kwon 등은[7] TiO2에서 관찰되는 저항변화 현상이 원 래의 TiO2 보다 산소결핍할 때 생기는 phase인 magneli 상 나노스케일의 필라멘트 형태로 상하부 전극을 연결하 면서 발생한다는 것을 투과전자현미경을 이용한 연구로 증명하였다. 이 과정에서 TEM으로 관찰한 magneli phase가 실제로 metallic한 behavior를 보일 수 있다는 것을보이기 위해서 conductive atomic force microscopy 를 이용하여 nanoscale의 magneli filament를 통한 conduction과 TiO2를 통한 conduction이 실제로 다르게 나타남을 실험적으로 보였다. 그림 11a는 이와 같은 분석 을 실시한 set-up의 schematic을 보여주며,그림 11b는 실제로 TiO2와 Ti4ᄋ7을 통해서 관찰된 conduction을 보여 준다. 그림 9b의 log-log plot으로부터 실제 Ti4O7의 경우 에 TiO2와달리 높은 전류밀도가관찰되며,전류와전압이 선형적인 관계를 가지는 ᄋhmic conduction이 나타남을 볼 수 있었다.
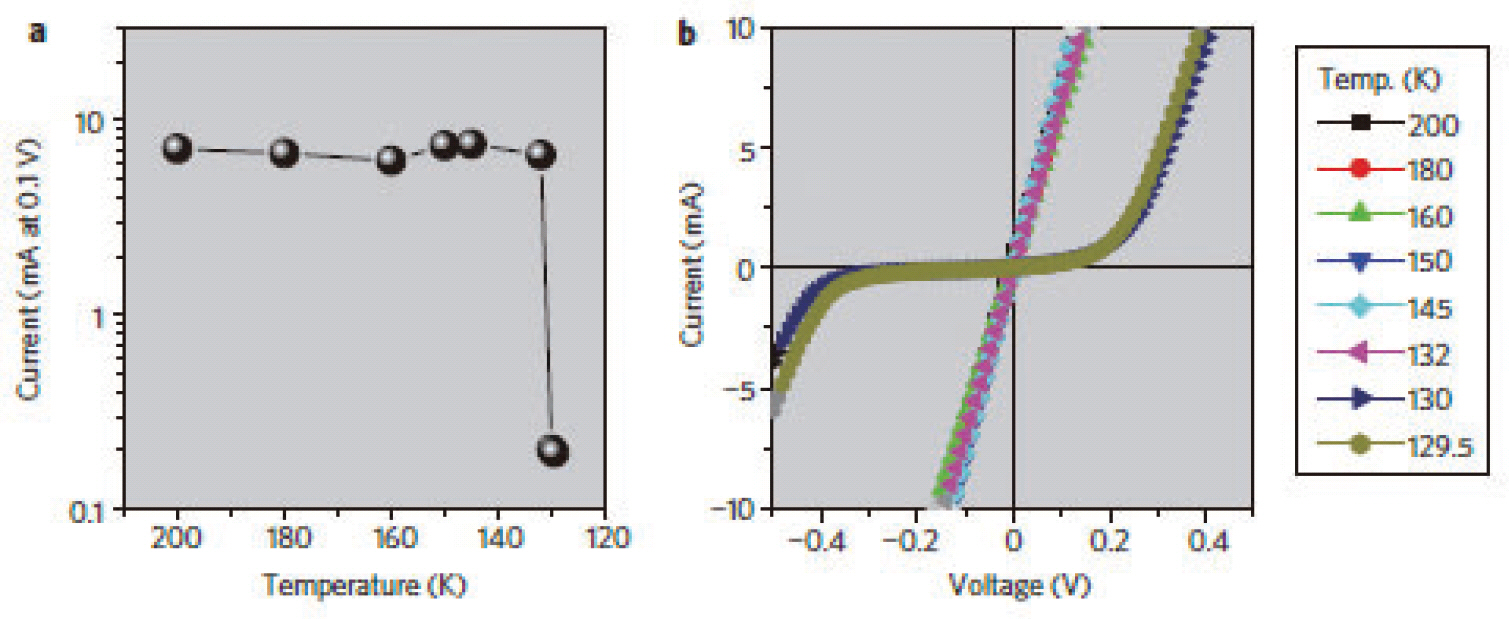
또한, magneli phase의 경우에 semiconductor/ metal transition이 약 150 K 부근의 온도에서 나타난다 는 것이 알려져 있는데,magneli phase의 전기적 특성의 온도의존성을 평가하기 위한 실험을 실시하였다. 그 결과 가 그림 10a와 b에 요약되어 있다. 그림 12a는 0.1V에서 측정된 여러 온도에서의 magneli filament를 통한 전류 값을 보여주며,그림 10b는 다양한 온도에서의 전류-전 압 곡선을 보여준다. 이로부터 약 130 K 정도의 온도에 서 실제 semiconductor—metal transition이 나타난다 는 사실을 확인할수있었다.[7]
2.2.4. Space—charge—limited conduction
Space-charge-limited conduction (SCLC)는 유전막으 로의 injection이 매우 강할 때 나타날 수 있는 conduction mechanism이다. 지금까지 기술된 conduction mechanism 들은 유전막 내부에 일정한 electric field가 걸리는 것으로 가정하고 기술되었으나,injection이 매우강한경우에는 더 이상 이 가정이 맞지 않게 된다. 따라서. 유전막 내의 potential distribution을 계산하기 위해서는 Poisson's law 를 도입해야 한다. SCLC의 경우에는 한가지의 식으로만 기 술되는 것이 아니라 전계의 크기에 따라서 여러 구간이 존 재하게 된다. 전계에 따른 여러 구간에 대해서는 아래에서 더 자세히 살펴보기로 한다
우선,charge injection이 약한 낮은 전압 영역에서는 electric field가전체 영역에서 균일하게 분포하게 된다. 즉, 유전막내에 space charge 영역이 특별히 존재하지 않는상 황이다. 이 때에는 식 8과같이 Ohm's law에 따르는 전류밀 도 값이 관찰된다. 식 8에서 n0는 평형 상태에서의 carrier concentration에 해당되며,이는 thermally generated carrier density가 외부에서 injection되는 carrier보다 많은 상태라는 것을 의미한다.
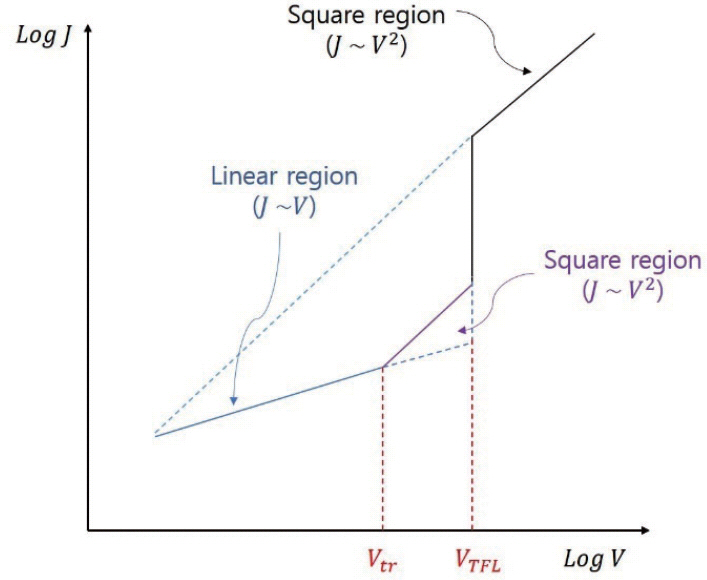
전계가 증가하여 더 강한 injection 상황이 되면 낮은 전압에서는 채워지지 않았던 유전막 내의 trap site들이 채워지면서 space charge region이 발생하기 시작한다. 약한 injection에서 강한 injection으로 넘어가는 Vtr의 전압은 carrier transit time과 dielectric relaxation time이 같아지며,외부에서 injection되는 carrier 농도 평형상태의 carrier 농도가 같아진다. V>Vtr일 때 외부에 서 injection되는 carrier의 transit time이 매우 짧아지 기 때문에 더 이상 thermally generated되는 carrier에 의해서 relax될 수 없다. 이에 따라서 유전막 내의 페르 미 준위 EF가 증가하여 electron trapping level보다 높 ΰ 에지게 된다.즉,유전막내의 trap 이 모두채워지는상 황이 되는데 이 전압이 trap-filled-limit voltage (Vtfl) 이다. Vtr에서 Vtfl 사이의 전압에서는 식 9를 따르는 conduction이 일어나며,식 9에서 볼 수 있듯이 전류밀 도는 전압의 제곱에 비례하는 꼴이 나타난다. 식 9에서 τηετα는 전체 carrier 밀도 중 free carrier 밀도의 비율 이다.
전압이 Vtfl 이상으로 증가하게 되면 모든 trap이 채워 져 있는 상태이므로,외부에서 주입되는 전자가 모두 free electron으로 conduction band 안에서 conduction 에 기여하게 된다. 그에 따라서 급격한 전류의 증가가 Vtfl 영역에서 발생하게 된다. 하지만,Ef가 conduction band minimum (Ec)에 가까워지게 되면서 다시 급격한 전류의 증가가 saturation되게 된다. 이 영역에서는 space charge에 의해서 conduction이 제한되게 된다. 그리고,식 10과 같은 Child's law를 따른 conduction이 나타나며,전류밀도는 전압의 제곱에 비례흐fe 영역이 다 시 나타나게 된다.
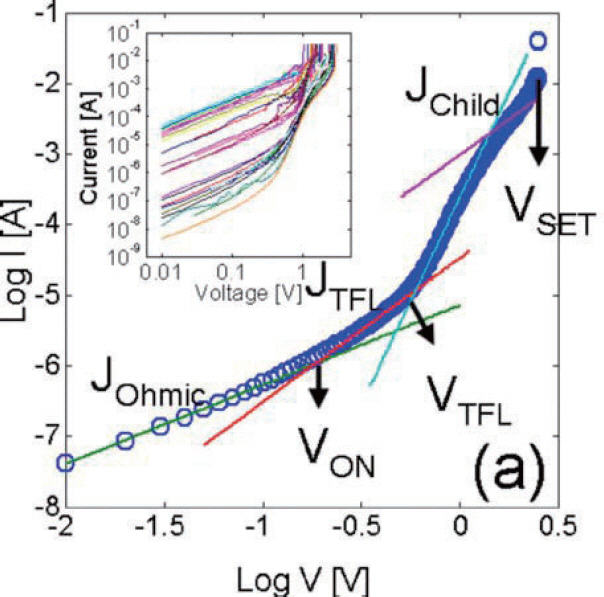
이상의 여러 구간에서의 변화를 종합해 보면 그림 9와 같이 요약할 수 있다. 즉,V〈Vtr인 낮은 전압 영역에서는 Ohm's law를 따라는 전압과 전류밀도가 선형관계를 가 지는 영역이 보인다. Vtr〈V〈VTFL인 영역에서는 전류밀도 가 전압의 제곱에 비례하는관계를 가진다. V=3DVtf일 때, trap이 모두 채워지면서 급격한 전류밀도의 증가가 나타 나며,V>Vtfl일 때 다시 space charge에 의해서 conduction이 제한되면서 전류밀도가 전압의 제곱이 비 례하는 영역이 다시 나타난다. 이런 특성 때문에 SCLC mechanism에 의한 conduction이 나타날 때에는 log-log plot을 이용한다. Log-log plot은 y=xn 꼴의 관계가 존재할 때에 n의 값을 기울기로부터 추측할 수 있는 특징 을 가진다. 즉,log(J)-log(V) plot을 해 보면 그림 13에 서 볼 수 있듯이 기울기가 1인 구간이 약한 injection 상 황에서 나타나며,Vtr 이상의 전압에서 기울기가 2인 구 간이 보이며,V=3DVtfl에서 급격한 전류밀도 증가 후 다시 기울기가 2인 구간이 나타나게 된다.
Metal-insulator-semiconductor stack에서 metal쪽에서 전자가 injection되어 Schottky emission이 나타날 때의 elec-tric band 모식도
이러한 SCLC 메커니즘은 저항변화 특성을 보이는 상 대적으로 oxygen vacancy 농도가 높은 ceramic 물질에 서도 관찰이 된다. Kim 등은[8] 저항변화 특성을 보이는 TiO2 유전막이 삽입된 Pt/TiO2/Pt stack의 캐패시터에 서 그림 14과같은 SCLC 메커니즘에 의한 conduction을 관찰하여 보고하였다. TiO2 박막의 경우에 filamentary switching mechanism을 통하여 low resistance state(LRS)와 high resistance state (HRS) 사이의 반 복적인 switching이 가능한 차세대 메모리 소자용 신소 재 중 하나이다. 그림 14에 표시되어 있는 Von 이 Vtr에 해 당되며,VSET은 HRS에서 LRS로 변하는 저항변화 전압 을 나타낸다. 실험 결과에 따르면,SCLC메커니즘이 저 항변화 현상 도중에 관찰되는 것을 볼 수 있었다. Kim 등 의 연구에서는 Vtr,Vtfl 등에서 계산이 가능한 space charge의 두께를 계산하였는데,이 값이 전체 박막의 두 께인 40 nm보다 훨씬 작은 3–10 nm 값이 나왔다. 이 결 과로부터 space charge층으로 여겨지는 얇은 두께 안에 서 conducting filament가 끊어지고,uniform하게 oxygen vacancy가 분포하는 영역이 존재한다는 것을 간접적으로 증명할 수 있었다.
3. Electric pulse를 이용한 전기적 분석 방법
전기적인 DC pulse를 가하면서 시간에 따른 전류를 실 시간으로 분석하는 방법이 최근 여러 연구분야에 적용되 어 흥미로운 결과들을 보여주고 있다. 이와 같은 방법은 직접적으로 재료 내부에 생기는 나노스케일의 미세한 변 화를 관찰하는 것은 아니지만,기존에 정립되어 있는 이 론들을 기반으로 재료 내부의 변화에 대한 가설을 합리적 으로 증명하는 데에 큰 역할을 하고 있다. 특히,강유전 체 박막에 대한 연구에서 해당 방법이 여러 선행 연구를 통해서 실제 박막 내의 물리,화학적 변화를 잘 설명할 수 있음이 보고되었다.[9–11] 본 장에서는 이러한 연구 결과 의 몇 가지 대표적인 예를 소개하며 electric pulse 측정 방법을 소개하고자 한다. 본 측정을 위해서는 다양한 형 태의 pulse를 정밀한 형태로 가할 수 있는 pulse generator와 pulse에 의한 response를 실시간으로 monitoring할 수 있는 oscilloscope가 일반적으로 사용 되며,자세한 실험 방법에 대해서는 상기 언급한 참고문 헌 10번을 참고하기를 권한다.
3.1. 강유전체의 negative capacitance 관찰
가장 기본적인 반도체 소자중하나이자스위치와같은 역할을 하는 device인 transistor의 성능은 전체 반도체 소자의 특성을 크게 좌우하는 매우 중요한 기본 소자이 다. 반도체 소자의 집적화가 진행되면서 transistor의 off current를 낮게 만드는 것이 점점 어려워지고 있고, 이런 문제를 하기 위해서 더 작은 전압 변화에서 큰 전류 변화를 만들 수 있는 transistor에 대한 연구들이 다수 진 행되고 있다. 이 중대표적인 한가지 연구가 ferroelectric 의 negative capacitance를 이용하는 것이다.[12–19] 강유전체의 스위칭 과정 중에 강유전체 물질의 differential capacitance가 실제로 음의 값을 가지는 것 처럼 보이는현상이 여러 연구그룹에 의해서 관찰되고 있 고,이 물질은 transistor의 gate oxide로 사용함으로써 더 에너지 효율적인 반도체 소자를 만들기 위한 노력이 계속 되고 있다. 이 negative capacitance는 static한 즉 정 방법으로는 관찰이 매우 어렵고,대부분의 연구가 전 기적인 pulse를 가하면서 transient하게 나타나는 전류 를 분석하면서 진행되고 있다.
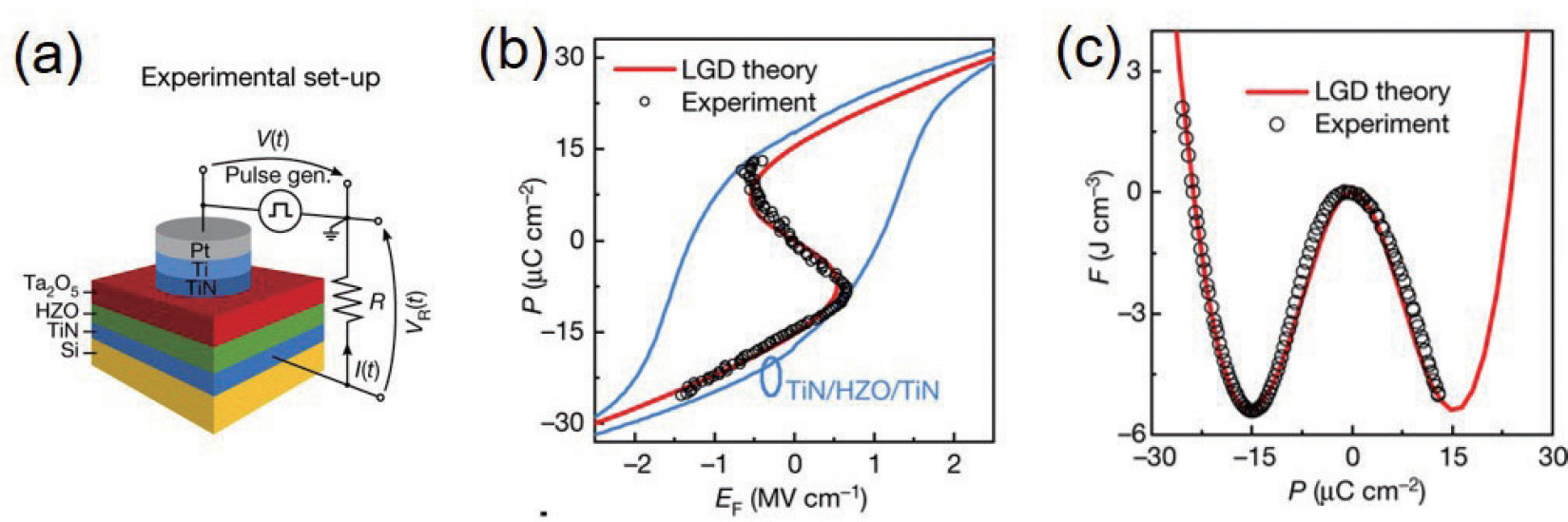
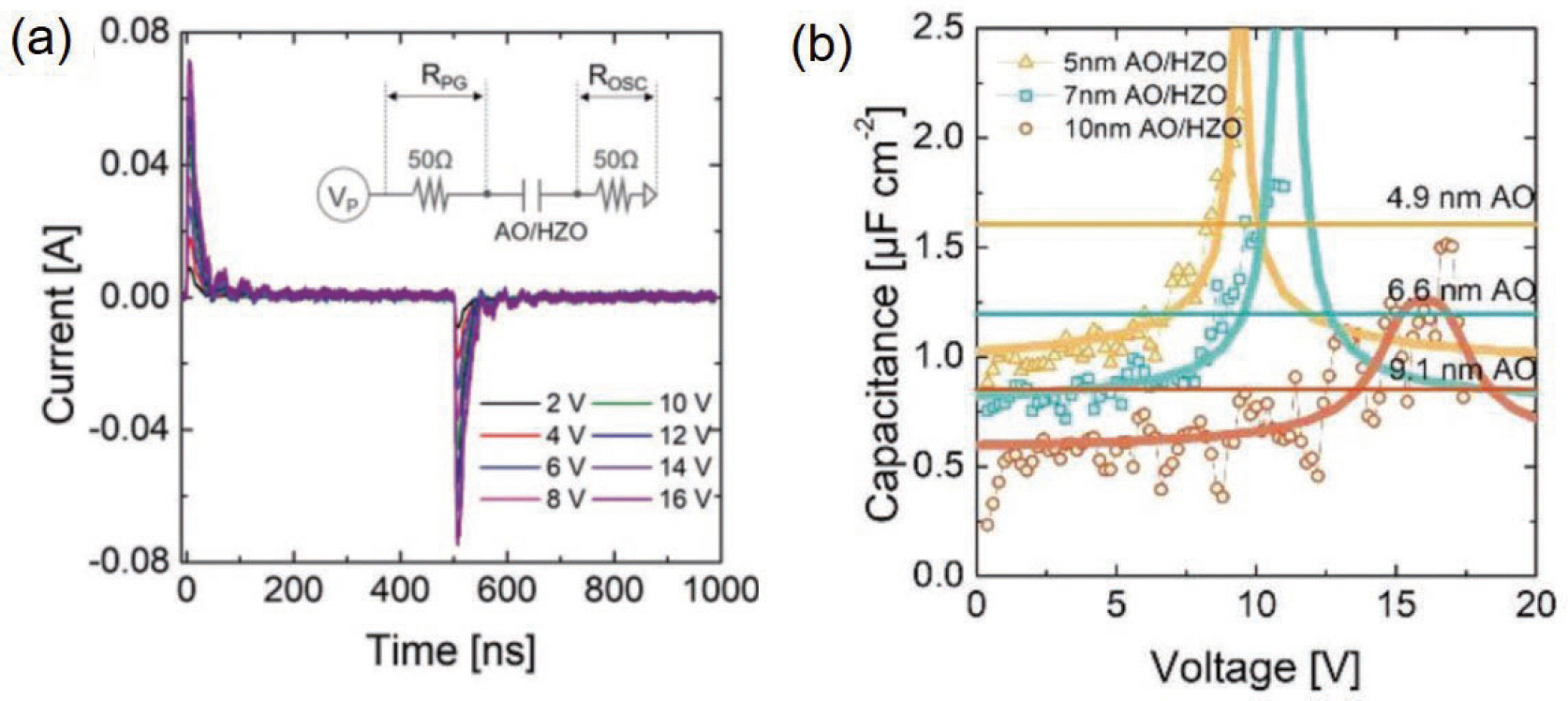
Hoffmann 등은[18] Hf0.5Zr0.5O2 (HZO)라는 강유전성 신소재를 이용하여 negative capacitance 현상을 electric pulse를 가하면서 나타나는 current를 이용해 분석하고자 하였다. 그림 12a는 측정에 사용된 캐패시터 소자와 회로 의 모식도를 보여준다. 그림 15a에서 볼 수 있듯이 유전막 으로는 HZ0/Ta205의 이중층구조가 사용되었다. 회로를 살펴보면 pulse generator에 측정하려는 캐패시터 샘플 에 직렬로 oscilloscope의 저항이 연결되어 있어,이 저항 에 흐르는 전류로부터 저항에 걸리는 전압을 읽고,pulse generator에서 실시간으로 읽는 전체 전압과의 차를 구하 면 캐패시터에 걸리는 전압을 계산할수 있다. Landau 이 론에서 기대되는 은자 모양의 polarization-electric field curve (그림 15b)와 이를 적분하여 얻을 수 있는 double well 형태의 free energy-polarization (그림 15c)를 관찰 할 수 있었다. 그림 12b에서 음의 기울기를 가지는 0V 부 근의 영역,15c에서 음의 곡률을 가지는 Pr=3D0 부근의 영역 이 negative capacitance 영역에 해당된다. 하지만,이는 컴퓨터 시뮬레이션 등으로 계산한 결과에서 기대되는 HZO의 Landau 상수와 비교하면 훨씬 작은 값이라서,실 제로는 domain에 의한 스위칭이 나타나면서 관찰된 것으 로 추측된다.
Kim 등은[19] Hf0.3Zr0.7O2/Al2O3의 이중층 구조의 유 전막을 적용한 캐패시터에서 역시 pulse 측정을 통하여 강유전체층에 걸리는 전압과 oscilloscope를 통해서 읽히 는 전류를 함께 분석하여 Hf0.3Zr0.7O2/Al2O3의 이중층 구 조의 캐패시턴스 값을 구하고,이를 Al2O3 단일층에서 기 대되는 캐패시턴스 값과 비교하였다. 그림 16a는 측정을 위해 사용된 모식도와 여러 전압에서 관찰된 시간에 따른 전류 변화를 보여준다. 그림 16b에서 볼 수 있듯이 모든 두께의 Al2O3에서 단일 Al2O3보다 。교다.7ᄋ2/신2ᄋ3의 이중층 구조의 캐패시턴스가 더 큰 영역이 관찰되었다. 이는 직렬연결되어 있는 강유전체층의 캐패시턴스가 음 의 값을 보였다는 실험적 증거가 된다.
강유전체의 negative capacitance는 실제 응용되었을 때 가질 수 있는 큰 파급력 때문에 사람들의 큰 관심을 받고 있 는 특성이지만,실제 static한 실험을 통해서는 관찰하기가 매우 어렵다.
하지만,electric pulse룰 이용한 transient response 분 석은짧은시간 영역에서 실시간으로분석을할수 있다는장 점이 있어,transient negative capacitance를 관찰하기에 적합한 방법이다. 따라서,현재 다수의 연구자들에 채택되 어 음의 캐패시턴스 연구에 활용되고 있다.
3.2. 강유전성 HfO2 기반 박막의 wake-up effect 연구
산화하프늄 기반 박막에서 나타나는 강유전성은 기존 강유전체와 비교해서 매우 얇은 두께에서도 우수한 특성 을 가지는 소자를 만들기에 적합하며,ALD와 같은 공정 으로 3차원의 나노 구조 위의 증착이 용이하고,Si이나 TiN 등의 반도체 산업의 표준 물질과 잘 맞는다는 점에 서 큰 관심을 받고 있는 신소재이다.[20–27] 하지만,아 직까지 소재의 반복적인 스위칭시의 신뢰성에 있어서 문 제가 있고,그 중 대표적인 문제가 wake-up effect라는 효과이다. 이 효과는 반복 스위칭을 하면서 강유전체가 저장할 수 있는 전하의 양과 직결되는 잔류분극 값이 증 가하는 현상이다. 즉,초기에 강유전성이 최적화되어 있 지 않다는 것을 보여준다. 따라서,이 문제를 해결하기 위 해서는 wake-up effect가 나타나는 원인을 밝히는 것이 매우 중요한 부분이었다.
Kim 등은[27] 이러한 현상을 분석하기 위해서 TiN/ hzo/tin의 구조를 가지는 캐패시터를 제작하고 이 캐 패시터를 electric pulse 방법으로 electric field cycling 이전의 pristine 상태와 다양한 수의 electric field cycling 후에 분석하였다. (그림 17a) 이 방법을 통해서 다양한 횟수의 electric field cycling 후의 계면층의 비강 유전체층의 캐패시턴스 ((interfacial capacitance Ci) contact resistance (Rc),coercive field (Ec) 등울 주줄 하는 것이 가능하였다. 그림 17b는 다양한 횟수의 electric field cycling 후의 다양한 높이의 pulse 측정에 대한 current response를 보여준다. 그림 17c는 그림 17b에서 주줄한 switching current의 pre-exponential term (Ο을 전계의 함수로 plot하여 E。와 Rl값을 추출 하는 과정을 보여준다. 이와 같은 과정을 각 electric field cycling이후의 data에 대해서 분석한 결과가 up-down polarization switching,down-up polarization switching에 대해서 구한 결과가 그림 17d와 e에 각각 요 약되어 있다. Rc에는 큰 변화가 없는 반면에 Ci값의 증가 가 지배적으로 나타나며,Ec값도 약간 증가하는 경향을 공통적으로 볼 수 있다. Ci값의 증가는 계면층에 존재하 는 비강유전체층의 두께가 감소하는 것을 의미한다. 이로 부터 wake-up effect 도중에 나타나는 변화는 계면층의 비강유전체층의 두께가 감소하는 것이라는 것을 실험적 으로 증명할 수 있었다.
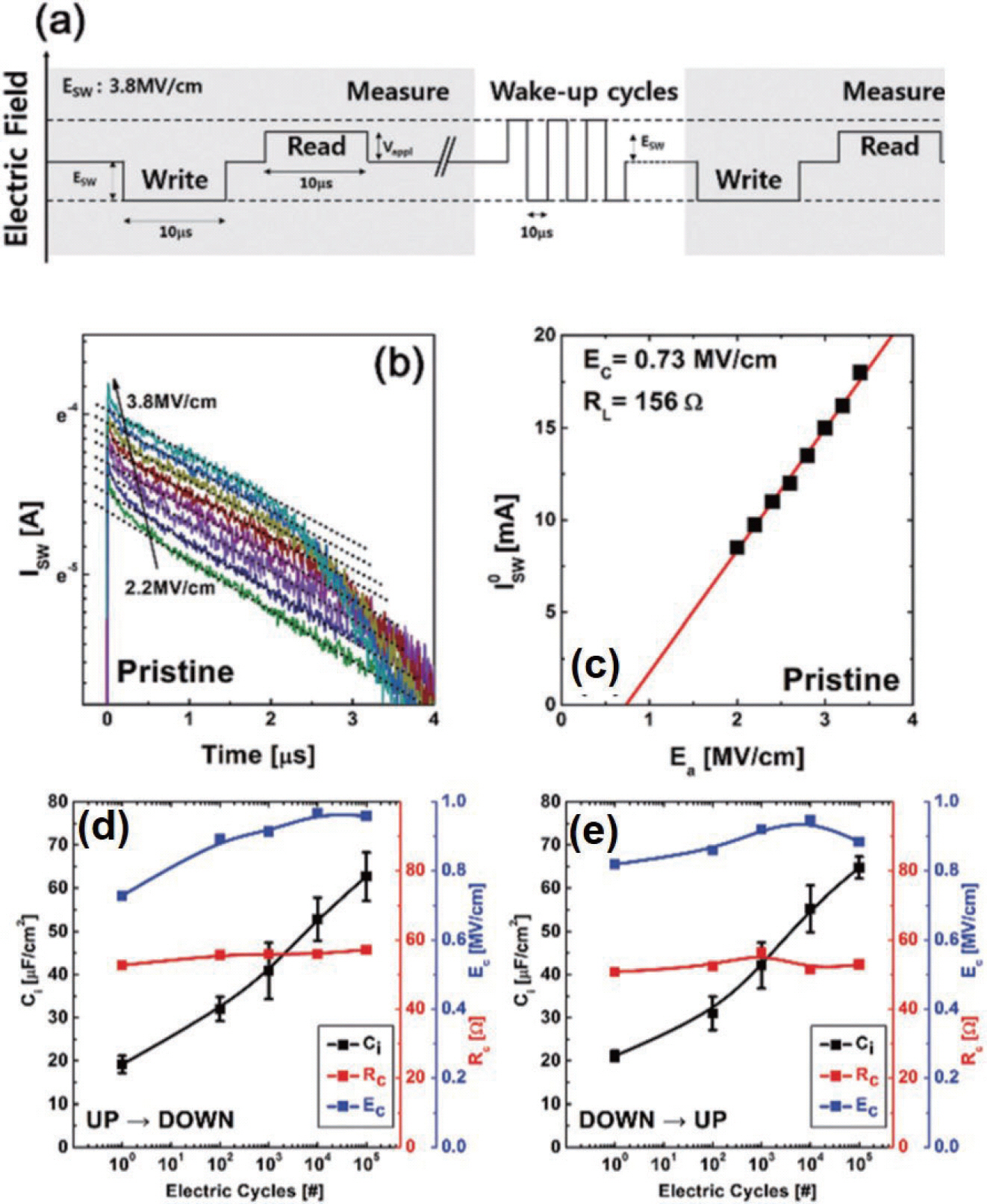
(a) 측정에 사용된 시간에 따른 전기적 펄스의 모식도. (b)시간에 대한 Hf0.5Zr0.5O2 박막의 switching current의 곡선. (c) (b)에서 측정 된 스위칭 전류 특성으로부터 추출된 초기 스위칭 전류값 (Isw 0)을 가해준 전계에 대해 plot한 그림. 이로부터 저항값과 coercive field가 추출 가능하다. (d) up-down 스위칭시와 (e) down-up 스위칭시의 여러 electric field cycling 횟수 후에 추출된 계면 캐 패시턴스 (Ci), 컨택저항 (Rc), 임계전계 (Ec)의 변화.[27]
강유전성 HZO 박막과 TiN의 계면층은 파괴적 분석방 법인 투과전자현미경 등의 방법을 사용하더라도 정확한 변화를 감지하기 어려운 나노스케일의 영역이다. 하지 만,샘플을 파괴하지 않고,electric pulse를 이용한 전기 적인 분석방법을 도입함으로써,강유전체층과 별도인 비 강유전체 계면층만의 캐패시턴스인 Ci값을 추출할 수 있 었고,이 값의 변화가 증가하는 현상으로부터 비강유전체 층의 두께가 감소한다는 것을 확인할 수 있었다. 또한,정 량적으로 비강유전체층의 결정상으로 알려진 tetragonal phase의 유전상수를 40 정도로 가정하였을 때 계면층의 두께는 약 1 – 2 nm의 매우 reasonable한 값이 추출됨 을 확인할 수 있었다.
3.3. 저항변호물질 TiO2에서의 filament 형성 kinetics 규명
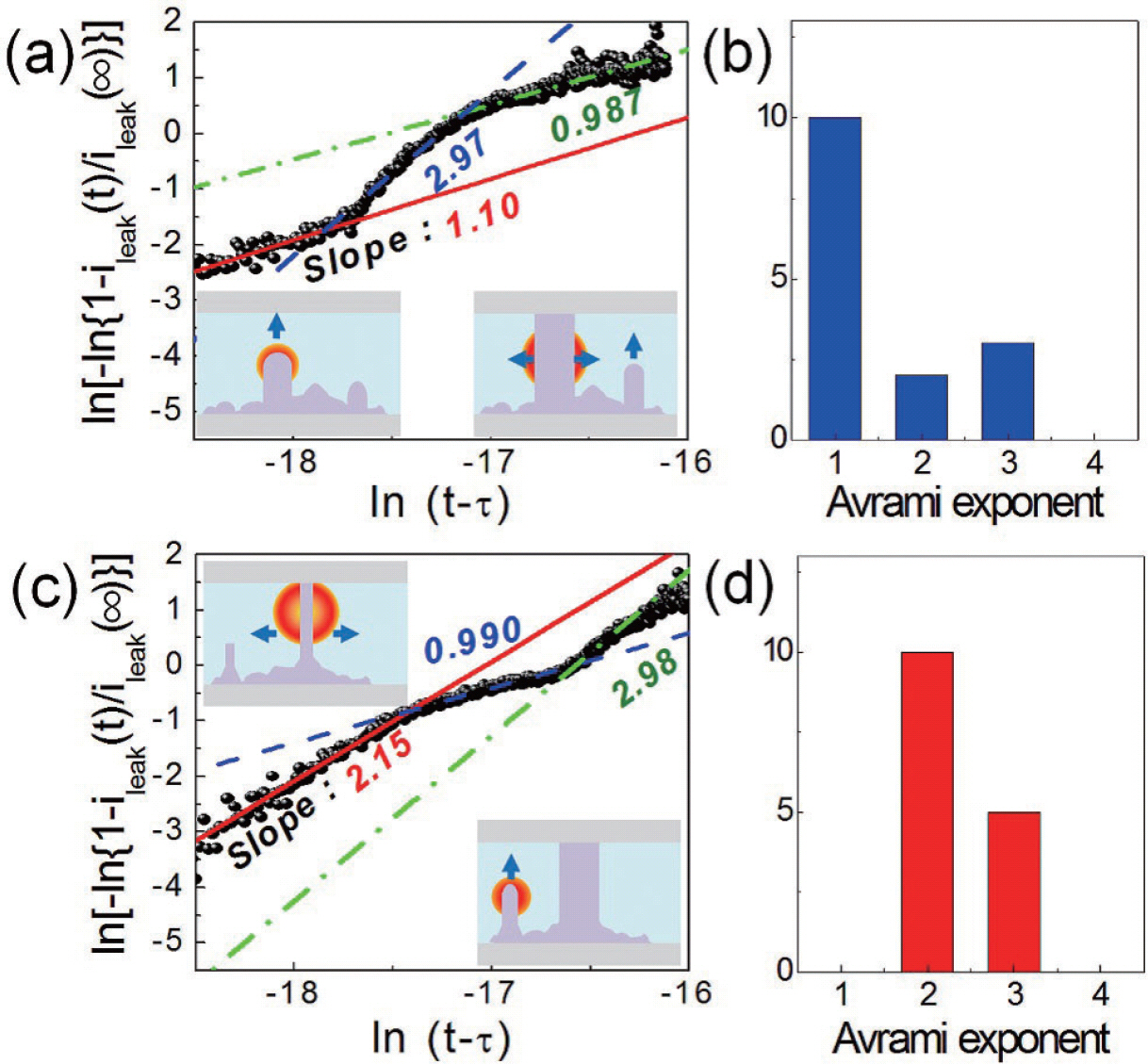
TiO2는 특유의 산소 결핍된 magneli상의 필라멘트의 형성으로 인해서 차세대 메모리 물질로 각광받는 신소재 중 하나이다.[28–31] Song 등은[31] TiO2에서 관찰되는 저항변화 현상을 일정한 높이의 electric pulse를 가할 때 시간 증가에 따라 나타나는 전류의 변화로부터 TiO2 내부 에 형성되는 filament의 성장 kinetics를 규명하기 위한 연구를 진행하였다. 필라멘트다 전통적인 상전이의 모델 인 Johnson—Mehl—Avrami (JMA) model을 따라서 성 장한다고 가정하였고,필라멘트의 부피비가 저항값과 직 결되는 상황을 가정하였다. 이러한 가정 하에서 JMA model과 같이 전류의 형태를 부피비에 결부시키고 Arrhenius 식을 적용하면 그림 15a와 c와 같이 ALD로 증착된 샘플과 sputtering으로 증착된 샘플에 대해서 저 항변화 양상을 관찰할 수 있었다. 그 과정에서 기울기가 변하는 구간이 나타나며,이 기울기는 Avrami exponent 즉,filament의 성장 dimension을 보여준다. 즉,n 차원 의 성장이 나타날 때 기울기 n이 나오게 된다. 분석 결과 ALD 박막에서는 상대적으로 저차원의 filament 성장이 관찰되었으나 스퍼터링 증착된 경우는 2–3차원의 성장 이 주로 관찰되었다. 저항변화 물질의 필라멘트의 경우 nm 스케일의 크기와 전체 부피에서 차지하는 면적이 작 은 점 때문에 파괴적인 분석방법이 TEM을 써야 많은 시 도를 통해 관찰할 수 있을 정도로 직접적인 관찰이 어렵 다. 하지만,Song 등의 연구에서는 외부에서 전기적인 펄스에 대한 response current를 읽음으로서 상전이를 실시간으로 평가할 수 있다는 점에서,전기적인 펄스 분 석의 새로운응용을 제시한중요한 의미를 가지는 연구라 할 수 있다.[31]
4. 결론
본 리뷰에서는 차세대 반도체 소자용 세라믹 박막에 대 한 전기적 분석 방법들을 최신 연구결과들과 함께 리뷰하 였다. 특히,세라믹 박막을 통한 conduction mechanism 을 분석한 연구들과 pulse 측정을 통하여 재료 내부의 미 세한 변화를 비파괴적으로 연구한 내용을 주로 살펴보았 다. 본 리뷰에서 다루어진 것처럼 세라믹 박막에는 다수의 conduction mechanism이 존재한다. 이러한 conduction mechanism은 전계의 값에 따라서 한 물질에서도 다양한 mechanism이 나타날 수 있으며,온도가 변하면서 mechanism이 변할 수도 있다. 또,유념할 점은 다양한 conduction mechanism이 동시에 나타날 수 있지만,그 중 특정 mechanism이 정량적으로 dominant할 경우 그 특정 mechanism이 관찰된다는 것이다. 즉,두 개 이상의 conduction mechanism이 정량적으로 비슷한 order의 값을 가지고 함께 conduction에 기여한다면 그 영역은 1 개의 model을 적용하여 설명하기 어려운 경우가 나타날 수도 있다. 또한,단순히 정성적으로 전류밀도와 전압,온 도와의 관계의 함수를 확인하는 것이 conduction mechanism을 완벽히 증명하기 충분하지 않다는 것도 유 념해야 한다. 즉,fitting에서 얻을 수 있는 유전상수, electron effective mass, barrier height, trap depth, trap spacing 등의 다양한 parameter들이 정량적으로 reasonable한 값을 보이는 것까지 확인이 되어야 conduction mechanism을 확실히 분석했다 할 수 있다. 또한,electric pulse를 측정한 분석을 통해서는 static한 분석방법으로 관찰이 어려운 강유전체의 transient negative capacitance와 같은 현상과 재료 내부의 미세한 상전이에서 기인하는 산화하프늄 기반 강유전체의 wake-up effect,저항변화 물질 내부의 산소결핍 필라멘트의 형 성 등을 비파괴적으로 분석하는 것이 가능하였다. 이처럼 다양한 전기적 특성 분석법들은 최신분석기법으로도 분석 하기 어려운 미세한 변화까지도 이론적 모델에 기반하여 분석하는 것이 가능하였다. 앞으로도 이러한 분석방법들 은 전자 소자용 재료에서 발생하는 다양한 변화를 이해하 는데 기여할수 있을 것으로 기대된다.
사사
이 과제는 부산대학교 기본연구지원사업(2년)에 의하 여 연구되었음.
References
Biography

◉◉이 동 현
◉2013년 – 현재 부산대학교 재료공학부 학사과정

◉◉양 건
◉2014년 – 현재 부산대학교 재료공학부 학사과정

◉◉박 주 용
◉2016년 – 현재 부산대학교 재료공학부 학사과정

◉◉박 민 혁
◉2018년 – 현재 부산대학교 재료공학부 조교수
◉2015년 – 2018년 독일 NaMLab 박사후 연구원
◉2016년 – 2018년 Humboldt Postdoctoral Fellow
◉2016년 – 2016년 Dresden Junior Fellow
◉2014년 – 2016년 서울대 재료공학부 BK21+ 연수연구원
◉2008년 – 2014년 서울대 재료공학부 석사 및 박사
◉2001년 - 2008년 – 2008년 서울대 재료공학부 학사