고열전도성 나노 소재 특성 분석 기술
Measurement Technique for High Thermal Conductivity Nanomaterials
Article information
Abstract
Abstract
With the development of the electronics industry, the trend of miniaturization raises the problem of heat management in electronic devices. Nanomaterials with high thermal conductivity are considered as an ideal candidate material for thermal dissipation applications due to their thermal properties. In this review, we introduce thermal measurement methods at nanoscale and discuss recent experimental results of the thermal properties of carbon nanotubes, graphene, and hexagonal boron nitride (h-BN). The various approaches in this paper could provide an opportunity to understand the principle of the measurement techniques and be more interested in thermal management applications.
1. 서론
지난 세기 동안 전자제품은 고성능화, 소형화되고 있으며, 더욱 좋은 성능을 갖기 위한 고밀도 집적화 연구 가 지속되고 있다.1,2) 반도체 소자는 1970년대부터 무어의 법칙에 따라 트랜지스터의 수가 1년 6개월마다 2배로 폭발적으로 늘어났다.3) 최근에 들어서는 트랜지스터 수의 증가 속도 점차 느려지고 있다. 그 이유 중 하나는 반 도체 소자에서 발생하는 열을 효과적으로 제어하지 못하는 것이다.4) 반도체 소자의 온도가 올라가면 전자의 흐름을 제어하는 저항, 축전기 등이 영향을 받아 작동 범위를 벗어날 수 있어 오작동 및 고장의 원인이 되기도 한다.5) 전기 자동차의 보급으로 배터리, 모터 등과 같이 높은 출력을 갖는 전자 기기의 수요가 증가함에 따라 제어해야하는 열의 양이 커지고 있으며, 온도를 제어하지 못하는 경우에는 배터리 화재와 같은 심각한 문제가 발생할 수 있다.6) 기존의 전자 기기와 높은 전력을 사용하는 전기 자동차 등의 수요가 증가함에 따라 효율적인 열 제어 기술에 대한 중요성이 점차 부각되고 있다.
열 제어 기술, 또는 방열 설계는 온도를 모니터링 하고 냉각하여 전자 기기의 회로나 베터리와 같은 기기의 온도를 작동 가능한 온도로 제어하는 것을 의미한다. 즉, 전자 기기의 열이 발생하는 곳에서 열을 제거하여 공기 등으로 방출해 내는 것이 방열 설계라고 할 수 있다. 방열 설계는 온도 컨트롤러, 액체/공기 냉각 시스템, 방열판 및 열 접촉 재료 (Thermal interface material, TIM) 로 구성된다. 방열량을 높이기 위해서는 각각의 파트에서 다음 기능을 담당하는 파트로 열이 빠르게 전달되어야 한다. 빠른 열전달을 위해서는 각각의 구성 요소의 소재를 열전도율이 높은 재료를 사용하여 고성능 방열판 및 고성능 TIM 를 제조하는 것이다.7)
기존에 알려진 최고의 열전도도 값을 뛰어넘는 나노 소재의 발견으로 고성능 방열 소재 적용에 대한 기대가 높다. 2001년 1차원 탄소 소재인 carbon nanotube(CNT)의 발견을 시작으로 2차원 물질인 그래핀, 질화붕소(BN) 등은 기계적 강도가 우수하며 열전도도가 높다고 알려졌다.8–17) 2,000 W m−1 K−1의 높은 열전도율을 가지고 있는 벌크 흑연, 혹은 다이아몬드를 능가하는 CNT, 그래핀과 같이 4,800–5,300 W m−1 K−1의 고열전도도를 갖는다고 보고되었다. 이와 같이, 높은 전기전도성 과 높은 열전도성를 동시에 갖는 나노 소재의 발견은 방열 기술에 사용되는 금속을 대체하고 더 좋은 성능의 방열 소재로의 가능성을 보여준다. 전기전도성과 열전도성이 동시에 높은 그래핀과는 달리 육각형 구조의 질화 붕소 (h-BN)은 전기 절연성이 뛰어 나면서도 열전도성이 높다. 이러한 특성은 전기 절연이 필요한 많은 전자 기기에서의 열 제어 소재로 h-BN 이 탁월한 대안이 될 수 있음을 의미한다. 그 결과, CNT, Graphene, h-BN 과 같은 소재들은 열 관리18,19), field-effect 트랜지스터20,21), 광 검출기22,23), 태양광 모듈24,25), 에너지 저장 장치26,27), 촉매28,29) 등 광범위한 응용 분야에서 큰 잠재력을 보여주었다.
이 논문에서는 나노 소재의 열 특성을 측정하기 위해 사용되는 기술과 그 기술을 통해 측정된 소재의 열전도도에 대해 정리해 보고자 한다. 우선적으로 나소 소재의 경우 열전도도를 측정하는 것이 어려워 개발된 다양한 방법에 대해 알아보고자 한다. 그 후, 개발된 측정 방법들을 이용해 측정된 나노 소재의 열 특성에 대해 알아보고자 한다. 이 과정을 통해 나노 소재의 열 전송 특성에 대해 소개할 수 있는 기회가 되었으면 한다.
2. 열전도도 측정 방법
이 섹션에서는 소재의 열전도도 측정 방법을 간략히 알아보려고 한다. 열전도도의 측정은 전기전도도의 측정과 유사한 부분이 많다. 그래서 친숙한 전기전도도와 비교를 통해 이해를 돕고자 한다. 전기전도도와 열전도도는 전기저항과 열저항의 식으로 간략히 나타낼 수 있다. 전기저항은 다음과 같은 식으로 나타난다.
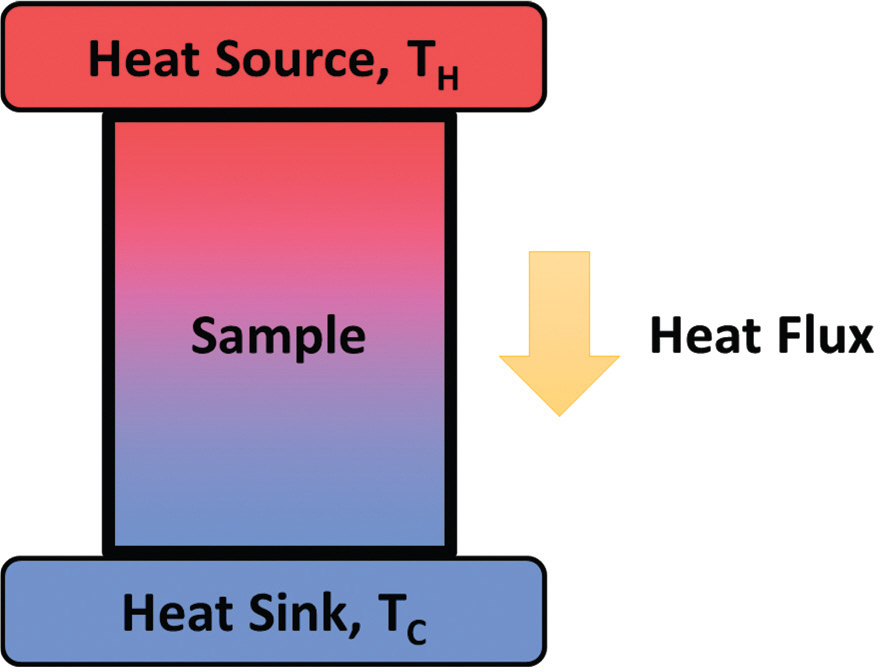
여기서 R electric은 소재의 전기저항, V는 소재에 가해지는 전압, I는 소재에 가해지는 전류이다. Fig. 1에서 보는 것과 같이 소재의 열저항은 Fourier 식을 통해 다음과 같이 나타난다.
여기서 R thermal은 소재의 열저항, Q는 heat flux, 그리고 T h, T c는 소재의 양끝의 온도이다. 전기전도도와 열전도도 모두 식 (1), (2)에서 와 같이 소재를 통해 흐르는 전기의 양(전류), 혹은 열의 양(heat flux)를 측정한다면 전기전도도와 열전도도를 계산해 낼 수 있다.
전기의 흐름인 전류는 측정하는 소재를 제외한 부분이 절연 소재로 이뤄진다면 측정하고자 하는 소재를 통해서만 전기는 흐르게 된다. 하지만, 열전도도 측정의 경우 측정하고자 하는 소재를 통해서만 전달되는 열량을 정확히 알아내기가 어렵다. 그 이유로는 열을 전달하는 방식이 전도(conduction), 대류(convection), 복사(radiation) 으로 3가지이고, 각각의 열 전달 방식을 제어하는 것이 어렵기 때문이다. 전도는 고체를 통해 흐르는 열 전달 방식이다. 측정하고자 하는 소재에 접촉해 있는 모든 것(기판, 측정을 위한 장치 등)으로도 전도를 통해 열의 흐름이 분산될 수 있다. 또한, 공기중에 있는 것 만으로도 열이 흐르는 대류 그리고 진공 상태에서도 열이 전달 되는 복사와 같이 세 가지 열 전달 방식을 모두 제어해야 측정하고자 하는 소재를 통해 흐르는 열량을 정확하게 측정할 수 있다. 특히, 나노 소재의 경우에는 소재의 크기 작아 소재로 흐르는 절대적인 열량이 작아 측정하기 어렵고, 추가적으로 대류와 복사와 같이 측정에 영향을 줄 수 있는 열 전달 방식에 대한 이해가 필요하다. Fig. 1에서 보는 것과 같이 열전도도의 측정에 필요한 소재의 양 끝에서의 온도도 소재의 크기가 작아지면서 정확하게 측정하는 것이 점점 더 어려워진다.
이런 어려움을 극복하고 나노 소재의 열전도도 측정을 위해 다양한 기술들이 개발되었다. 다양한 기술들은 측정을 위해 측정 원리에 맞게 소재를 준비해야하며 각 각의 방법에는 장단점이 있다. 이 챕터에서는 대표적인 나노 소재의 열전도도 측정 방법에 대해 알아보고자 한다. 이 챕터에서 소개할 열전도도 측정 방법을 소재에 열을 주는 방식에 따라 개발된 방법을 분류하였다. 소재에 열을 주는 방식으로는 대표적으로 3가지 방법으로 나눌 수 있다. 마이크로 칩을 활용한 방법, 광원을 이용한 방법, 소재에 전류를 흘려 소재의 발열을 이용하는 방법이다. 이 챕터를 통해 각 측정 방법의 원리를 이해한다면 새로운 물질의 열 전송 특성 분석을 위한 적합한 측정 방법을 찾을 수 있을 것으로 기대한다.
2.1. 마이크로 칩을 활용한 측정 방법
Fig. 2.에서 보는 방법이 마이크로 칩을 활용한 대표적인 두가지 방법이다. 하나는 두개의 떠있는 패드를 이용한 방법으로 2-pad 방법이라고 불린다. 그리고 다른 하나는 떠있는 한 개의 금속 히터와 측정하고자 하는 소재를 T자 형태로 겹쳐 놓아 측정하는 방식으로 T-bridge 방법이라고 불린다.
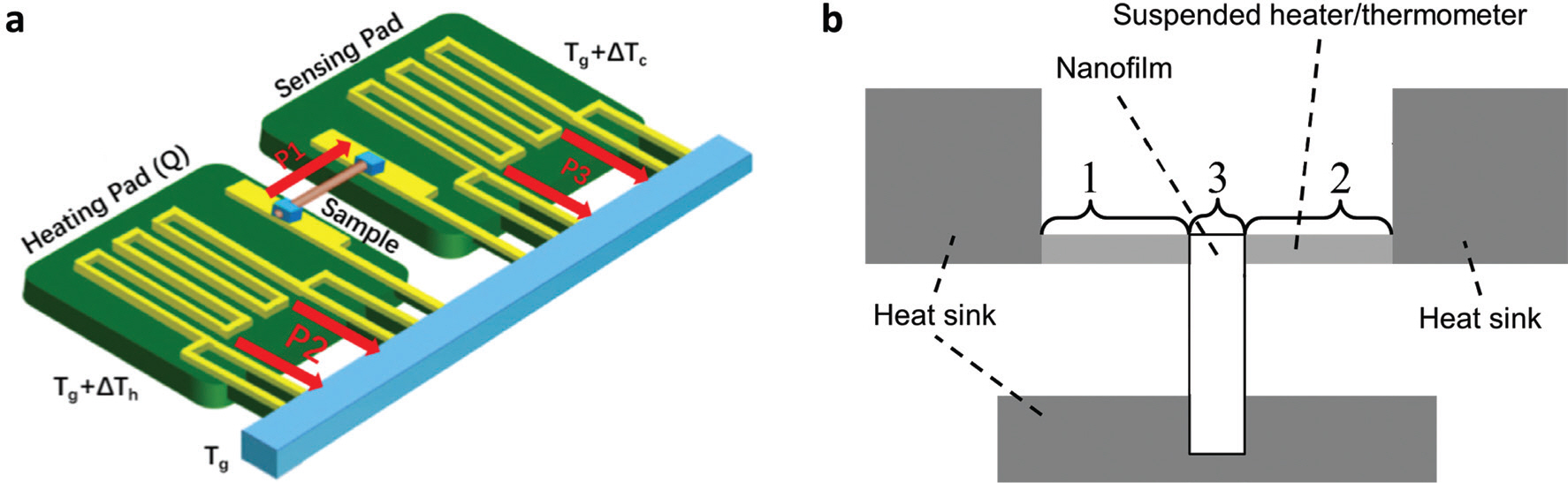
마이크로 칩을 활용한 열전도도 측정방법 a) 2-pad 열전도도 측정 방법 Adapted from Song et al. Joule 2018;2:442–463, with permission of Elsevier 59), b) T-bridge 열전도도 측정 방법. Adapted from Kim et al. Rev. Sci. Instrum. 2017;88:054902, with permission of AIP Publishing 38)
2-pad은 2001년 한 개의 MWCNT의 열전도도를 측정하면서 개발되었고 가장 널리 사용하고 있는 방법이다.30) Fig. 2a에 보이는 두 개의 패드는 각각 질화 실리콘(SiN x) 막으로 제작하며, 각 패드에는 패턴 된 금속 (백금)을 증착한다. 두 패드에 패턴 된 금속은 히터와 온도계로 사용된다. Fig. 2a에서 볼 수 있듯이 각 패드는 열의 흐름을 제어하기 위해 금속(백금)으로 코팅된 질화 실리콘(SiN x) 빔에 의해 매달려 있는 형태로 제작되어 패드에서 발생하는 열은 빔을 통해서만 기판으로 전달되는 구조를 갖는다. 이런 구조를 통해 소재 외에 기판으로 가는 열의 이동을 제어할 수 있다. 두 패드 중 한 쪽은 heater 로 작용하고 다른 한쪽은 cold side로 온도차이를 만들어 주는 역할을 한다. 소재의 양 끝의 온도는 금속의 저항이 온도에 따라 변하는 것을 이용해 각각의 패드의 패턴 된 금속의 저항 변화를 통해 온도를 측정할 수 있다. Fig. 2a에 화살표를 보면 떠있는 패드를 통하여 heating 패드에서 소재를 통해 전달된 열은 cold-side 패드로 전달되고, 빔에 의해 전체적인 기판으로 전달된다. 즉 cold-side에서 기판으로 전달되는 열량이 소재를 통해 흐른 열량이 된다. 이렇게 떠있는 2 개의 패드를 이용하여 소재의 양끝 온도와 소재를 통해 흐르는 열량을 측정하여 열전도도를 측정하는 방법이 2-pad 방법의 원리이다.
이 방법의 온도 측정 원리인 금속의 저항을 이용하여 온도를 측정하는 방법은 미세한 온도(0.05 K)까지 정밀하게 온도를 측정할 수 있어 측정의 정확성이 높다.31) 일차원 나노 물질 같은 경우 패드와 소재가 선으로 접촉하고 있어 소재와 패드 사이의 열 접촉 저항을 줄이기 위해 Focus ion beam 장비로 추가적인 접촉 면을 만들어 주기도 한다. 이 방법이 개발된 이후, 소재와 패드에서의 열 접촉 저항을 알아내거나 Wheat-stone bridge 방법을 통해 온도 측정의 정밀성을 향상 시키는 등의 측정 정확도를 향상시키기 위한 다양한 시도가 이루어졌다. 32–34) 2-pad 방식은 그래핀, h-BN, MoS2, BP, Bi2 Te3 등 다양한 나노 소재의 열전도도 측정에도 활용됐다. 35–37) 이 방법은 측정의 정확성이 높으나 떠 있는 두 패드 위에 나노 소재를 위치 시키는데 어려움이 있고, 마이크로 칩을 제작하는 과정 또한 복잡하다.
T-bride 방법은 떠 있는 금속에 T 모양으로 측정하고 싶은 소재를 올려놓아 붙여진 이름이다. Fig. 2b에서 가운데 길게 연한 회색으로 나타나 있는 부분이 길게 패턴 된 금속이고 그 중간에 나노 선, 나노 필름 등의 소재를 올려 측정하게 된다.38–40) 기판을 제외한 금속과 측정하려는 소재는 열의 이동을 제어하기 위해 떠 있는 형태로 측정을 진행한다. 나노 소재가 올라가지 않은 상태에서 떠있는 금속만 있을 때 금속에 전류를 흘리면 금속에서 저항에 의한 Joule 열이 발생하고 금속에서 발생한 열은 기판으로 흐르면서 금속의 온도가 올라가게 된다. 이 때에 온도가 올라가는 정도로 히터 역할을 하는 떠있는 금속의 열전도도를 측정할 수 있다.41) 떠 있는 금속의 열전도도를 측정한 후, 금속 위에 나노 소재를 Fig. 2b에 보이는 것과 같이 T자 모양으로 올려놓고 같은 전류를 흘리면, 소재를 통해 열이 흐르는 만큼 금속의 온도가 낮아지게 된다. 소재가 있는 경우와 없는 경우의 떠있는 금속의 온도 상승의 차이를 가지고 나노 소재의 열전도도를 계산하게 된다. 직접적으로 소재 양단의 온도를 측정하고 소재를 통해 전달된 열량을 측정하는 2-pad 방법과는 다르게 소재에 열을 가해주는 역할을 하는 금속 온도 변화를 통해 올라간 소재의 열전도도를 측정하는 방식이다.
이 방법은 또한 처음에는 일차원 나노 소재의 열전도도를 측정하기 위해 개발되었으며, 나중에 이차원 나노소재에도 적용가능하게 발전되었다.38) 이 방법은 AC 가열 전류를 사용할 경우 열 접촉 저항의 영향을 제거할 수 있어 정확한 나노 소재의 열전도도를 측정할 수 있다.
2.2. 광원을 이용한 측정 방법
Fig. 3.에서 보는 방법이 광원을 이용한 두가지 방법이다. 하나는 Raman spectrum을 이용하여 소재의 온도를 측정하는 방법이고, 다른 하나는 금속의 반사도와 온도와의 상관 관계를 이용하는 time-domain thermal reflectance 방법이다.

광학적 방법을 통한 열전도도 측정방법 a) Raman spectrum 열전도도 측정 방법, b) TDTR 열전도도 측정 방법. Adapted from Song et al. Joule 2018;2:442–463, with permission of Elsevier 59)
Raman spectrum을 이용한 기술은 2008년 Balandin 그룹에서 떠있는 한층 그래핀의 열전도도를 측정하기 위해 처음 사용하였으며, 4,800–5,300 W m−1 K−1의 열전도도로 측정되었다.10) 이 측정에서는 Fig. 3a에서 보는 것과 같이 소재의 중앙에 쏘아주는 레이저를 통해 소재로 흡수된 열을 통해 측정하는 방식이다. 소재의 중심에 흡수된 열은 떠있는 소재를 통해 기판으로 전달된다. 이 과정에서 소재가 열을 잘 전달하는 경우 소재의 온도가 낮아지고, 열을 잘 전달하지 못하는 경우에 소재의 온도가 높아진다. 소재의 온도 측정은 광학적인 방식인 Raman spectrum을 이용한다. Raman spectrum의 peak은 소재의 온도에 따라 선형으로 변하는 상관 관계를 보여주는 경우를 활용하여 Raman spectrum의 peak의 위치 변화로 소재의 온도를 알 수 있다. 레이저를 통해 흡수된 열량과 소재의 온도 상승 정도를 통해 소재의 열전도도를 계산할 수 있다.
최초의 그래핀 측정 이후에 많은 연구자들이 그래핀의 열전도도를 동일한 방식으로 그래핀의 두께에 따라서 측정하였다.17) 이 방법은 기판에 떠 있는 소재가 있는 간단한 구조로 h-BN42), MoS243,44) 와 같은 다른 2D 재료의 열전도도를 측정하기 위해 범용적으로 사용되고 있다. 단, Raman spectrum 방법은 상대적으로 실험 오차가 크다. 실험 오차는 측정하고자 하는 소재로 레이저를 통해 흡수되는 정확할 열량에 대한 오차, 레 이저 크기에 따른 흡수 면적에 대한 부분, 소재와 기판 사이 발생하는 열 접촉 저항이 원인이 될 수 있다. 이런 부분을 개선하기 위해 대류로 인한 열 손실을 제거하는 등 오차를 줄이기 위한 노력이 지속적으로 진행되고 있다.31,45) 하지만, 온도 측정 방법인 Raman spectrum의 peak과 온도의 상관 관계가 금속 저항의 변화로 온도를 측정하는 것에 비해 큰 오차를 가지고 있는 점이 이 측정 방법의 오차를 줄이는데 한계를 가지고 있다.
Time-domain thermal reflectance(TDTR) 측정 방법은 나노 소재의 두께 방향(cross-plane)으로의 열 전달을 측정하는 방법이다. 1986년 최초로 개발되었지만 46) 2000년대에서야 나노 소재 기술의 발전과 함께 최근 몇 년 동안 광범위하게 연구되었다.47) 이 측정에서는 Fig. 3b에서 보는 것과 같이 두 가지 레이저 “펌프” 빔과 “프로브” 빔을 사용한다. 펌프 빔을 통해 가열된 시편의 온도 변화를 프로브 빔을 통해 측정하여 열전도도를 측정하는 방법이다. 프로브 빔을 통해 소재의 온도를 측정하는 원리는 금속의 반사도가 온도에 따라 변화는 원리를 이용기 때문에 측정하고자하는 소재 위에 얇은 금속 코팅 혹은 증착이 필요하다. 측정하는 과정은 우선 펌프 빔을 통해 금속 표면에 약 3∼5 K 정도의 온도로 가열한다. 프로브 빔을 통해 금속의 반사율 변화로 표면의 온도 변화를 모니터링 한다. 측정이 완료되고 모니터링 된 소재의 시간에 따른 온도 변화를 통해 수학적 모델링을 통해 소재의 두께 방향의 열전도도를 측정하는 방식이다.
프로브 빔과 펌프 빔 사이의 위상 및 진폭 등의 시간 지연을 이용하여 소재의 시간에 따른 온도 변화를 10−9초(ps) 스케일로 분석할 수 있어 아주 작은 온도 변화도 감지할 수 있으며, 두께 방향의 측정이기 때문에 소재와 기판 계면 사이에서의 열 접촉 저항도 측정할 수 있다.48) 측정 방법의 장점을 살려 그래핀과 금속 사이에서의 열 저항에서도 다양한 연구가 진행되었다.49,50) 이 방법으로 BP와 WSe2와 같은 이차원 소재에서의 두께 방향으로의 열전도도를 측정이 보고되었다.51,52)
2.3. 소재의 발열을 이용한 열전도도 측정 방법
Fig. 4에 나타나 있는 소재 자체에 열을 가해주는 방식은 전류를 가하여 소재에서 발생된 Joule 열을 열원으로 이용한다. 이 때 소재의 온도를 측정하는 방식으로 두가지 방식으로 나눌 수 있다. 소재 자체의 전기 저항의 변화로 소재의 온도를 측정하는 방법과 적외선 카메라를 이용하여 소재의 온도를 직접적으로 측정하는 방법으로 나눌 수 있다. 이 소재의 양 단을 통하여 전류를 흘려주는 단순한 방식으로 나노 소재에서부터 섬유 형태의 소재까지 다양한 복합 소재에서도 사용되고 있다. 이 방법은 소재의 Joule 열을 이용하기 때문에 소재는 전기 전도성 물질이어야 하는 점에서 다양한 소재를 측정하지 못하는 한계가 있다.

소재 자체의 발열을 이용한 열전도도 측정방법 Adapted from Pop et al. Nano Lett. 2006;6:96–100, with permission of ACS publications a) 온도에 따른 저항 변화를 활용하는 방법 12), b) IR 카메라를 이용하여 소재의 온도를 측정하는 방법. Adapted from Jang et al. Nanoscale 2018;10:17799–17806, with permission of Royal Society of Chemistry 60)
소재 자체의 전기적 신호를 이용하여 소재의 온도 및 열 특성을 분석하는 기술로는 DC와 AC전류를 이용하는 두가지 방법으로 나눌 수 있다. 이 방법도 소재에서 다른 물질을 통하여 전달되는 열을 차단하기 위해 소재는 띄운 상태에서 측정이 진행된다. Fig. 4a에서 보는 것과 같이 정확한 측정을 위해 소재에 4개의 전극을 만들고 양끝 전극에서 전류, 그리고 가운데 두 전극에서 전압을 측정하여 소재의 저항을 정확하게 측정할 수 있다. 가운데 두 전극 사이의 소재는 떠 있는 형태로 소재에서 발생하는 열은 소재와 맞닿아있는 기판을 통해 전달된다. 소재에서 발생된 열이 기판으로 전달되는 양에 따라 소재의 온도가 변하게 된다. 챕터 2.1에서 설명한 T-bridge 방법(Fig. 2b)에서 나노 소재가 올라가 있지 않은 떠 있는 히터만 있는 경우와 같은 측정 방법으로, 금속 대신 소재 자체를 측정하는 방법이다. AC 전류를 이용하는 경우에는 frequency에 따라 전압과 온도와의 상관관계로 인해 열전도도 이외에도 열 용량이라는 열 특성을 측정할 수 있는 장점이 있다.
소재의 온도를 적외선 카메라로 측정하는 방법은 접근성이 좋아 섬유형 소재를 측정하는데 많이 사용되었다. Fig. 4b에서 보는 것과 같이 2개의 전극을 이용하는 방법, 정확한 측정을 위해서는 위에서 설명한 Fig. 4a과 같이 4개의 전극을 이용하여 소재에 가해진 정확한 열량을 측정할 수 있다. 위에 방법과 같이 떠있는 소재에서 발생하는 온도를 Fig. 4b에 보는 것과 같이 적외선 카메 라를 통해 길이 방향으로 측정할 수 있다. 적외선 카메라를 통해 측정된 길이 방향의 온도 프로파일로 소재의 열전도도를 측정하는 방식이다. 이 방법은 나노 소재의 경우 적외선 카메라로 측정할 수 있는 한계가 있어 아주 작은 나노 소재에는 적용하기 힘들다.
이 방법은 적외선 카메라로 측정하는 소재의 온도의 정확성이 중요하다. 소재 별로 적외선을 방출하는 방사율(emissivity)가 달라 정확한 측정을 위해서는 각 소재의 방사율를 정확하게 알고 있어야 한다. 소재의 모양이나 크기가 작아짐에 따라 방사율이 변할 수 있어 정확한 측정을 위해서 측정하는 크기와 모양에 맞는 방사율을 측정하는 것이 중요하다.
3. 고열전도도 나노 소재
고열전도성 소재로는 탄소로 구성된 CNT, 그래핀, 그리고 그래핀과 같이 육각형 구조를 갖는 h-BN이 대표적이다. 이 챕터에서는 대표 물질인 CNT, 그래핀, h-BN 나노 소재의 열전도도 측정 결과에 대해 알아보고자 한다.
Table 1은 단일 벽 CNT(SWCNT)와 다중 벽 CNT(MWCNT)에 대한 실험 데이터를 정리해 놓은 것이다. Table 1에서 CNT의 열전도도는 1,100 ∼ 7,000 W m−1 K−1 범위로 측정된 것을 알 수 있다. CNT 열전도도 측정 결과는 7배 정도의 측정 값에 차이가 있는데, 이 차이는 CNT를 만드는 방법과 소재의 전기적 특성, 불순물 함량 정도, 실험 방법에 따른 오차 등으로 생긴 것으로 알려져 있다. 최근에 들어 일반적으로 CNT의 열전도도로 사용되는 값은 단일 벽 CNT(SWCNT)의 경우 3500 W m−1 K−1, 다중 벽 CNT(MWCNT)의 경우 3000 W m−1 K−1 이다. 12,14) 이 값은 벌크 그래핀의 열전도도인 2000 W m−1 K−1 에서 50∼75%의 열전도도가 증가한 값이다.
그래핀의 열전도도는 2008년에 광열 라만 기술로 Balandin이 처음 측정하였으며, Raman spectrum을 이용하는 광학적 방식으로 4,800–5,300 W m−1 K−1의 열전도도를 보여준다.10) Ghosh, Cai, Faugeras 등의 연구자들이 Raman spectrum 방법을 이용하여 그래핀의 열전도도를 값을 추가적으로 보고하였다. 각 각의 방식들은 그래핀의 측정의 정확도를 높이기 위해 진행되었다. Ghosh는 고품질 그래핀에서 얻어낸 대면적 그래핀을 측정하여 3,000 W m−1 K−1의 결과를 얻었다.53) Cai는 그래핀이 떠있을 때 기판의 아래 부분을 완전히 뚫어 그래핀을 통과하는 레이저를 측정하는 방식으로 Raman 방법을 보안하여 Chemical vapor deposition (CVD) 방법으로 합성된 고품질 그래핀의 열전도도를 350K에서 2500 W m−1 K−1, 500K에서 1400 W m−1 K−1으로 측정하였다.9) Faugeras도 Raman 방법을 이용하여 더 높은 온도까지 그래핀의 열전도도를 측정하였다.8)
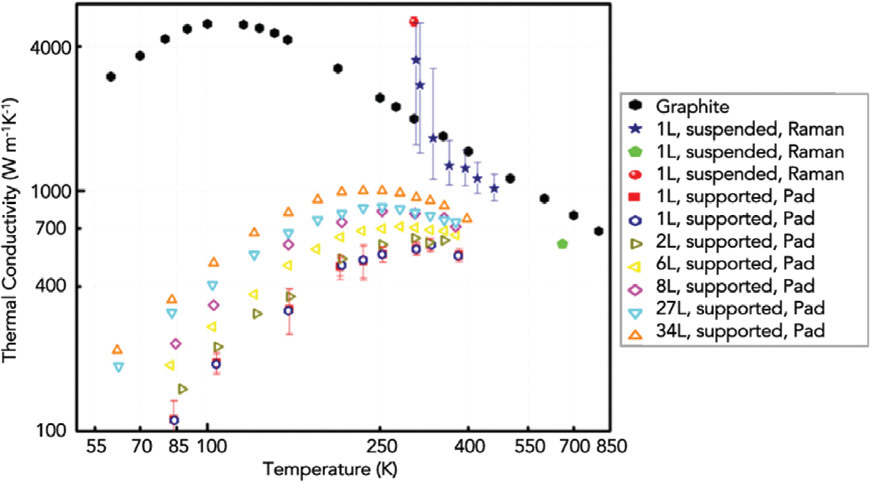
단층인 구조에서 열전도도가 높은 현상을 이해하기위해 그래핀의 층 수에 따른 열전도도에 대한 연구가 진행되었다. Ghosh는 그래핀의 한 층의 열전도도가 여러 층인 경우의 열전도도보다 높다고 처음 보고했다.17) 이 논문에서는 Raman spectrum 방법을 이용하여 그래핀 이 2층에서 4층으로 층이 증가함에 따라 2,800 W m−1 K−1 에서 1,300 W m−1 K−1로 그래핀의 열전도도가 감소한다고 보고하였다. Fig. 5에는 다양한 측정방법으로 측정된 그래핀의 열전도도 값을 보여준다. Fig. 5에는 Raman 방법으로 측정된 Balandin10), Lee45), Faugeras8) 의 결과가 들어있으며, 2-pad 방법으로 측정된 Seol54), Sadeghi55)이 나타나있다.
질화 붕소의 열전도도 결과는 Table 2에서 볼 수 있다. 그래핀의 열전도도가 측정되고 BN의 열전도도에도 많은 관심이 있었지만 이론적으로 계산된 열전도도가 실험적으로 증명되지 않았다. 최초로 보고된 여러 층의 h-BN에 대한 측정 값은 벌크 h-BN보다 작았다. Jo는 상온에서 각각 250, 360 W m−1 K−1 인 5층, 11층 h-BN의 열전도도를 2-pad 방법으로 측정했다.56) Zhou는 Raman spectrum 방법을 사용하여 CVD가 생성한 9층 h-BN의 열전도도가 227 ∼ 280 W m−1 K−1 범위에 있음을 보고했다.42) 같은 합성 방법으로 측정된 다양한 층에 대한 열전도도 측정 결과는 5층 h-BN이 11층 h-BN보다 열전도도가 낮다고 보고되어, 그래핀에서 열전도도가 각각 약 4000에서 약 2800으로, 1,300 W m−1 K−1 가 1층에서 2층, 4층으로 떨어지는 추세와는 정반대의 결과를 보여준다.
최근 Cai는 고품질의 한 층의 h-BN이 실온에서 751 W m−1 K−1의 열전도도를 갖는다고 Raman spectrum 방법을 이용해 보고했다. 그리고 이전의 결과에서 보는 것과 같이 h-BN이 얇아 짐에 따라 열전도도가 낮아지는 현상을 동일하게 보고하였다.57) 이 결과는 Raman spectrum 실험 중 h-BN이 팽창하여 길이가 변화하는 부분을 보정하여 더 높은 실험 결과를 얻을 수 있었다. Chen은 붕소의 동위원소를 제어한 입방 (cubic) 구조의 질화 붕소를 합성하고 열전도도를 TDTR 방법으로 측정하였다.58) 붕소의 경우 10, 11 두가지 질량을 갖는 원소들로 구성되나, 이 것을 각각 10, 11로만 제어하여 1600 W m−1 K−1의 열전도도 값을 측정하였다. 넓은 밴드 갭, 높은 열 전도성, 뛰어난 강도, 우수한 유연성, 우수한 열 및 화학적 안정성 때문에 BN에 대한 다양한 연구가 지속적으로 진행되고 있고, 특히 차세대 유연한 전자 기기에서 열 제어 응용분야의 강력한 소재 후보이다.
4. 맺음말
본 논문에서 알아본 것과 같이 소재의 열 특성 측정은 다양한 방법의 개발과 지속적인 향상이 있었음에도 불구하고 여전히 나노 소재에서의 열 특성에 대해 이해하지 못하고 있는 부분이 많다. 동일한 나노 소재의 열전도도가 측정 방법에 따라, 소재의 합성 과정 혹은 측정 준비 과정에 따라 큰 차이를 보고이는 것을 챕터 3을 통해 알 수 있다. 소재의 크기가 작고 측정 환경을 만들어 열의 이동을 제어하는 것이 어렵기 때문에 이런 다양한 결과가 나오는 것으로 생각한다. 이렇게 다양한 나노 소재의 열전도도에 대한 연구가 지속적으로 진행되고 있지만, 나노 소재의 경우 소재 자체의 크기가 작아 열전도도가 높아도 결과적으로 전달되는 총 열량은 크지 않다는 소재 사이즈에서의 한계를 가지고 있다. 이런 문제를 해결하기위해 복합 소재에 대한 관심이 늘어나고 있다. 다양한 측정 방법의 원리를 이해하고 나노 소재부터 다양한 복합 소재까지의 열전도도 측정 기술이 개발되어 나노 소재 및 복합 소재의 구성 및 구조에 따른 열 특성 분석 기술 발전과 열 제어 응용 분야에 더 관심을 갖는 기회가 되었으면 한다.
감사의 글
본 논문은 KIST 주요사업(2K02620, 2Z06541, 2Z06542)의 지원을 받아 수행되었음.
References
Biography

◉◉김 정 원
◉ 2016년 연세대학교 기계공학과 박사
◉ 2016년-2018년 나노구조물리연구단(IBS) 박사후연구원
◉ 2019년-2020년 한국화학연구원 박사후연구원
◉ 2020년-현재 한국과학기술연구원 선임연구원