ņä£ļĪĀ
ņĀä ņäĖĻ│äņØś ņŚÉļäłņ¦Ć ņłśņÜöĻ░Ć ņ”ØĻ░ĆĒĢśĻ│Ā ņ×¼ņāØ ļČłĻ░ĆļŖźĒĢ£ ĒÖöņäØ ņŚ░ļŻīņØś ņ¢æņØ┤ Ļ░ÉņåīĒĢ©ņŚÉ ļö░ļØ╝ ņ¦ĆņåŹ Ļ░ĆļŖźĒĢ£ ņ×¼ņāØ Ļ░ĆļŖź ņŚÉļäłņ¦ĆņøÉņŚÉ ļīĆĒĢ£ ĒĢäņÜöņä▒ņØ┤ ļČäļ¬ģĒĢ┤ņĪīļŗż. ņØ┤ļ¤¼ĒĢ£ ņŚÉļäłņ¦Ć ļ¼ĖņĀ£ņŚÉ ļīĆĒĢ£ ĒĢ┤Ļ▓░ņ▒ģņØĆ ļéŁļ╣äļÉśļŖö ņŚÉļäłņ¦ĆņØś ņ¢æņØä ņżäņ×äņ£╝ļĪ£ņŹ© ņŗżĒśäļÉĀ ņłś ņ׳ļŗż. ņĀäņäĖĻ│äņĀüņ£╝ļĪ£ ņāØņé░ļÉśļŖö ņŚÉļäłņ¦Ć ņżæ 41 %ļ¦īņØ┤ ņ£ĀņÜ®ņä▒ ņ׳ļŖö ņŚÉļäłņ¦ĆļĪ£ ņé¼ņÜ®ļÉśļ®░ ļéśļ©Ėņ¦Ć57.5 %ļŖö ņĄ£ņóģņĀüņ£╝ļĪ£ ĒÅÉņŚ┤ņØś ĒśĢĒā£ļĪ£ ļéŁļ╣äļÉ£ļŗż1. Ļ░Ćņן ĒÆŹļČĆĒĢ£ ļ»ĖĒÖ£ņÜ® ņŚÉļäłņ¦ĆņØĖ ĒÅÉņŚ┤ņØä ņ£ĀņÜ®ĒĢ£ ņĀäĻĖ░ ņŚÉļäłņ¦ĆļĪ£ ņ×¼ņāØņé░ĒĢ£ļŗżļ®┤ ļ»ĖļלņŚÉ ņŚÉļäłņ¦Ć ņłśĻĖēņØ┤ Ļ░£ņäĀļÉĀ ņłś ņ׳ļŗż.
ņŚ┤ņĀäņØĆ ļČĆĒö╝ļź╝ ņ×æĻ▓ī ļ¦īļōż ņłś ņ׳Ļ│Ā, ļö░ļØ╝ņä£ ņäżņ╣ś Ļ│ĄĻ░äņØś ņĀ£ņĢĮņØä ļŹ£ ļ░øļŖö ĒÅÉņŚ┤ ĒÜīņłś ĻĖ░ņłĀņØ┤ļŗż. ņŚ┤ņĀäņØś ņä▒ļŖźņØä ļéśĒāĆļé┤ļŖö Ļ░Ćņן ļīĆĒæ£ņĀüņØĖ ņ▓ÖļÅäļŖö ņŚ┤ ļ│ĆĒÖś ĒÜ©ņ£©ņØ┤Ļ│Ā, ņØ┤ļĪ£ļČĆĒä░ ļŗżļźĖ ņŚ┤ņĀä ņä▒ļŖźņŚÉ ļīĆĒĢ£ ņ▓ÖļÅäĻ░Ć ņ£ĀļÅäļÉ£ļŗż.
ņłśņŗØ 1ņŚÉņä£ ļéśĒāĆļé¼ļō»ņØ┤, ņŚ┤ ļ│ĆĒÖś ĒÜ©ņ£© (h)ņØĆ ņ╣┤ļź┤ļģĖ ĒÜ©ņ£© (( T H - T C T H ) ( ZT + 1 - 1 ZT + 1 + T C T H ) ( ZT + 1 - 1 ZT + 1 + T C T H )
ņŚ┤ņĀä ņןņ╣śņØś ĒÜ©ņ£©ņØä ĻĘ╣ļīĆĒÖöĒĢśļĀżļ®┤ ZTļź╝ ĻĘ╣ļīĆĒÖöĒĢ┤ņĢ╝ĒĢ£ļŗż. ļö░ļØ╝ņä£ ņŚ┤ņĀä ņ×¼ļŻīņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼ņØś ļīĆļČĆļČäņØĆ ZTļź╝ ļåÆņØ┤ļŖö Ļ▓āņØä ļ¬®Ēæ£ļĪ£ ĒĢśĻ│Ā ņ׳ļŗż. ĻĘĖļ¤¼ļéś ZTļź╝ ļåÆņØ┤ĻĖ░ ņ£äĒĢ┤ņä£ļŖö ĒĢ£ ņ×¼ļŻī ļé┤ņŚÉņä£ ņ×¼ļŻīņØś ņĀäĻĖ░ ņĀäļÅäļÅä (Žā), ņĀ£ļ▓Ī Ļ│äņłś (S), ņŚ┤ ņĀäļÅäļÅä (k)ņØś ņØśļ»ĖņÖĆ ĻĘĖļōż ņé¼ņØ┤ņØś ļīĆļ”Į Ļ┤ĆĻ│ä (tradeoff)ļź╝ ņØ┤ĒĢ┤ĒĢ┤ņĢ╝ ĒĢ£ļŗż.
ņŚ┤ņĀä ņ×¼ļŻīļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ ļåÆņØĆ ļåŹļÅäņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ (ņĀĢĻ│Ą ļśÉļŖö ņĀäņ×É, h+ ļśÉļŖö e-)ļź╝ Ļ░Ćņ¦ä ņóüņØĆ ļ░┤ļō£ Ļ░Ł ļ░śļÅäņ▓┤ (narrow band gap semiconductors)ņØ┤ļŗż. ņŚ┤ņĀä ņ×¼ļŻīĻ░Ć ņś©ļÅä ĻĄ¼ļ░░ļź╝ ļ░øņ£╝ļ®┤ ņ║Éļ”¼ņ¢┤Ļ░Ć ņ×¼ļŻīņØś ņ░©Ļ░ĆņÜ┤ ļČĆļČäņ£╝ļĪ£ ņØ┤ļÅÖĒĢśļŖö Ļ▓ĮĒ¢źņØ┤ ņ׳ļŗż (Fig 1). ņś©ļÅä ĻĄ¼ļ░░ņŚÉņä£ ņ║Éļ”¼ņ¢┤ ļåŹļÅäņØś ņØ┤ļ¤¼ĒĢ£ ļČłĻĘĀĒśĢņØĆ ņÜ┤ļÅÖ ņŚÉļäłņ¦ĆĻ░Ć ļé«ņØĆ ņĀĆņś©ņØś ņ║Éļ”¼ņ¢┤ļ│┤ļŗż Ļ│Āņś©ņØś ņ║Éļ”¼ņ¢┤Ļ░Ć ļŹö Ēü░ ĒÖĢņé░ Ļ│äņłś (diffusivity)ļź╝ Ļ░Ćņ¦ä ļŹ░ņä£ ļ╣äļĪ»ļÉ£ļŗż (Fig 2). ņŚ┤ņĀä ņ×¼ļŻīņØś ņĀĆņś©ļČĆņŚÉņä£ ņ║Éļ”¼ņ¢┤ņØś ŌĆ£ņČĢņĀüŌĆØņØĆ ņ×¼ļŻīņØś ļČĆļČä ļ│äļĪ£ ņĀäņĢĢ ņ░©ņØ┤ļź╝ ņāØņä▒ĒĢ£ļŗż. ļ¼╝ņ¦łņØś ņĀ£ļ▓Ī Ļ│äņłś (S)ļŖö ņłśņŗØ 3ņŚÉņä£ ļ│╝ ņłś ņ׳ļō»ņØ┤ ņŻ╝ņ¢┤ņ¦ä ņś©ļÅä ĻĄ¼ļ░░ (D T)ņŚÉ ņØśĒĢ┤ ņāØņä▒ļÉ£ ņĀäņĢĢ (D V)ņØś Ēü¼ĻĖ░ļź╝ ņĀĢļ¤ēĒÖöĒĢ£ļŗż. ĻĘĖļ¤░ ļŗżņØī ņ×¼ļŻīĻ░Ć ņÖĖļČĆ ļČĆĒĢśņŚÉ ņŚ░Ļ▓░ļÉśņ¢┤ ņĀäļźśĻ░Ć ĒØÉļź┤ļ®┤ņä£ ņĀäļĀź ņČ£ļĀźņØä ņāØņä▒ĒĢ£ļŗż. ņŚ┤ņĀä ņ×¼ļŻīļŖö ņĀäĻĖ░ ņŚÉļäłņ¦Ć ņĀĆņן ļŖźļĀźņØä Ļ░Ćņ¦ĆĻ│Ā ņ׳ņ¦Ć ņĢŖĻĖ░ ļĢīļ¼ĖņŚÉ ņłśĒÖĢļÉ£ ņĀäļĀźņØĆ ņāØņé░ļÉ£ ļÅÖņŗ£ņŚÉ ņåīļ╣äļÉśņ¢┤ņĢ╝ļ¦ī ĒĢśĻ│Ā, ĻĘĖļĀćņ¦Ć ņĢŖļŗżļ®┤ ļéŁļ╣äļÉĀ ļ┐ÉņØ┤ļŗż. ļśÉĒĢ£ ņłśņŗØ 3ņŚÉņä£ ļéśĒāĆļé¼ļō»ņØ┤, ņ║Éļ”¼ņ¢┤ ļåŹļÅäĻ░Ć ļé«ņØäņłśļĪØ ņĀ£ļ▓Ī Ļ│äņłśļŖö ņāüņŖ╣ĒĢ£ļŗżļŖö ņĀÉņŚÉ ņŻ╝ļ¬®ĒĢĀ ĒĢäņÜöĻ░Ć ņ׳ļŗż (ļ░śļÅäņ▓┤ ņŚ┤ņĀä ņ×¼ļŻīņØś Ēżļ¼╝ņäĀĒśĢ ļ░┤ļō£ļź╝ Ļ░ĆņĀĢ)2.
Fig.┬Ā1.
ņŚ┤ņĀä ĒÜ©Ļ│╝ļŖö ĻĖłņåŹņØ┤ļéś ļ░śļÅäņ▓┤ņÖĆ Ļ░ÖņØĆ ņĀäļÅäņä▒ ņ×¼ļŻīņŚÉņä£ ļ░£ņāØĒĢ£ļŗż. ņś©ļÅä ĻĄ¼ļ░░Ļ░Ć ņŻ╝ņ¢┤ņĪīņØä ļĢī, ņ×¼ļŻī ļé┤ļČĆņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļŖö ņś©ļÅäĻ░Ć ļé«ņØĆ ņ¬Įņ£╝ļĪ£ ĒÄĖņżæļÉ£ļŗż (polarized). ņØ┤ļŖö ņ×¼ļŻī ļé┤ņØś ņś©ļÅä ņ░©ļź╝ ļö░ļØ╝ ņĀäņ£ä ņ░©, ņ”ē ņĀäņĢĢņØä ņāØņä▒ĒĢśĻ│Ā, ņØ┤ļŖö ņĀäĻĖ░ņĀü ņØ╝ļĪ£ ļ│ĆĒÖśļÉĀ ņłś ņ׳ļŗż.
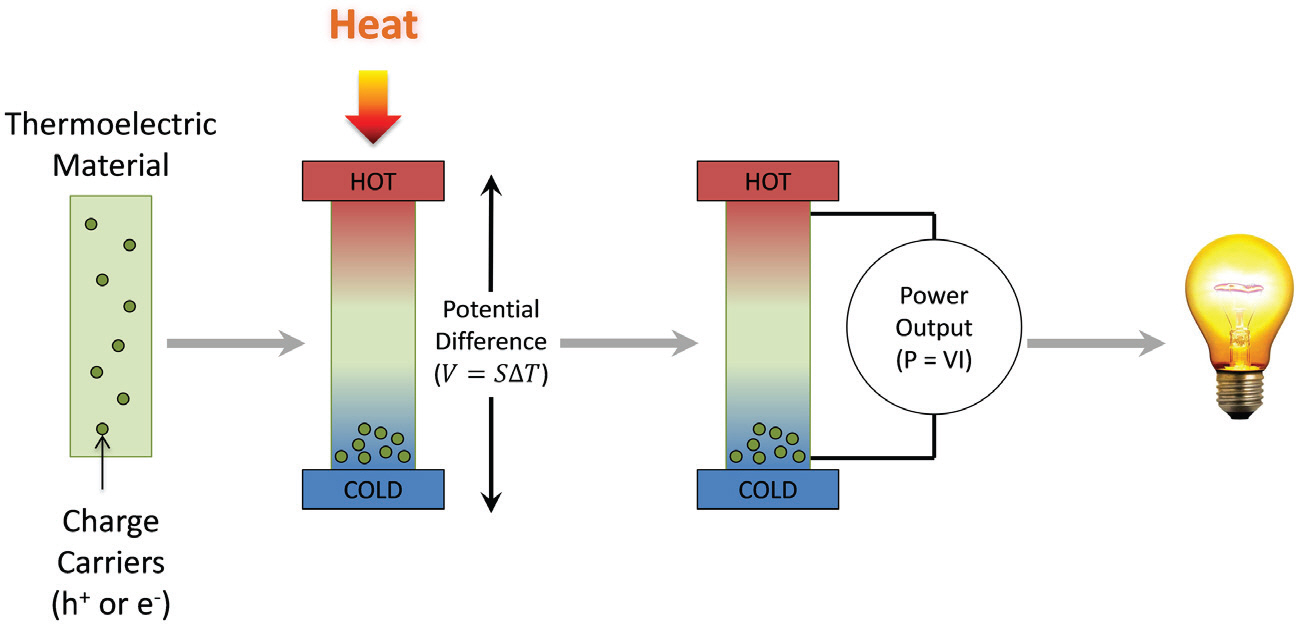
Fig.┬Ā2.
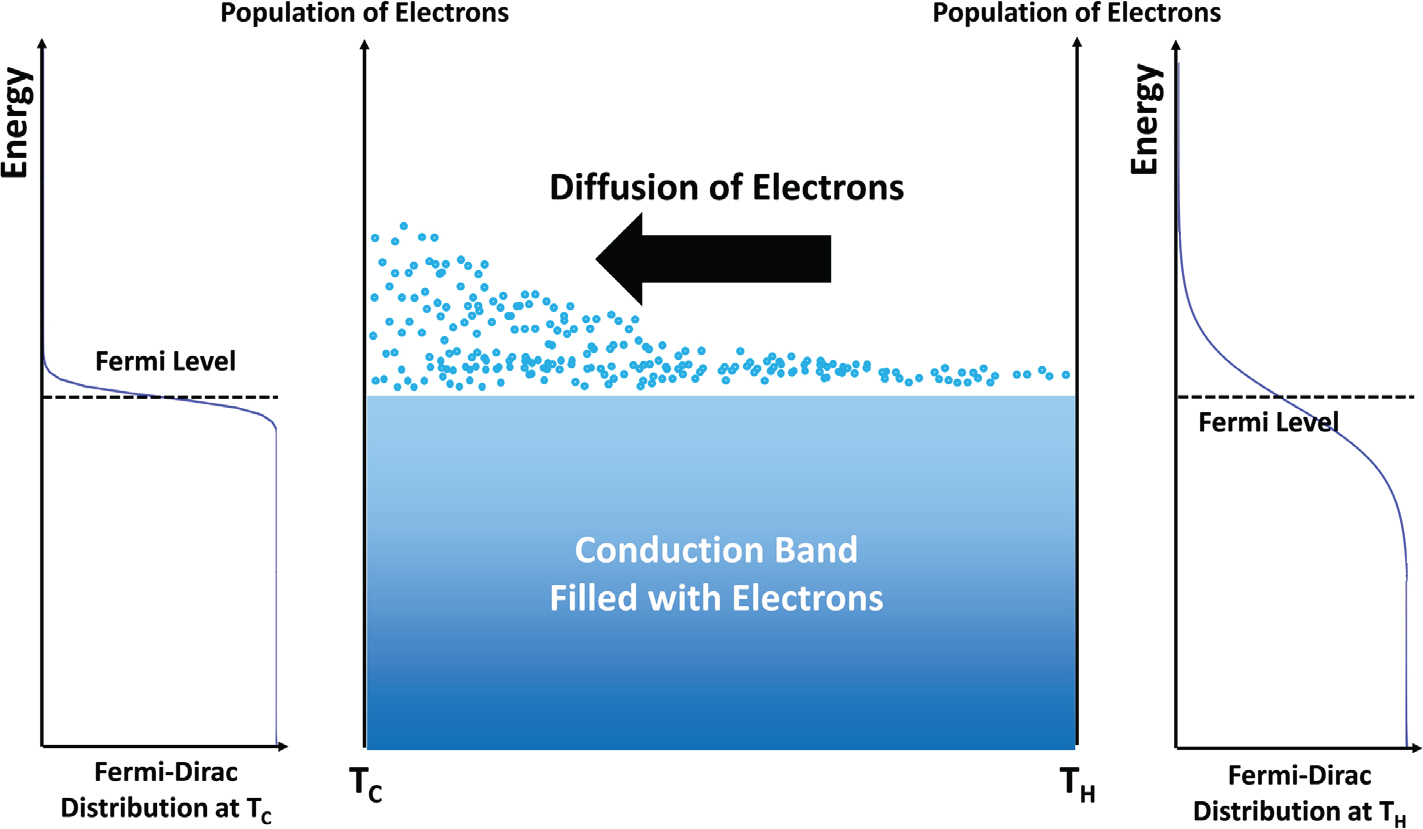
ņŚ┤ņĀä ņ×¼ļŻīņØś ņØ╝ņóģņØĖ ĻĖłņåŹņŚÉņä£ņØś ņĀ£ļ▓Ī ĒÜ©Ļ│╝ļź╝ ļ»Ėņŗ£ņĀüņØĖ Ļ┤ĆņĀÉņŚÉņä£ ļéśĒāĆļéĖļŗż. Ļ│Āņś© (T H) ņ¬ĮņŚÉ ņ׳ļŖö ņ×Éņ£Ā ņĀäņ×ÉļŖö ņĀĆņś© ņ¬ĮņŚÉ ņ׳ļŖö ņ×Éņ£Ā ņĀäņ×ÉņŚÉ ļ╣äĒĢ┤ ĒÅēĻĘĀņĀüņ£╝ļĪ£ ļŹö ļåÆņØĆ ņÜ┤ļÅÖ ņŚÉļäłņ¦Ć, ņ”ē ĒÅēĻĘĀņĀüņ£╝ļĪ£ ļŹö Ēü░ ņåŹļÅäļź╝ Ļ░Ćņ¦äļŗż. ĒåĄĻ│äņĀüņ£╝ļĪ£, ņĀäņ×ÉļŖö ņ░©Ļ░ĆņÜ┤ ņ¬Įņ£╝ļĪ£ ĒÄĖņżæļÉśĻ│Ā, ņĀäņ×ÉņØś Ļ│ĄĻ░äņĀü ĒÄĖņżæņØĆ ņĀäņĢĢņØä ņØ╝ņ£╝Ēé©ļŗż. Ļ░ÖņØĆ ĒśäņāüņØ┤ ļ╣äļŗ© ĻĖłņåŹ ļ┐É ņĢäļŗłļØ╝ ļ░śļÅäņ▓┤ņŚÉņä£ļÅä ņØ╝ņ¢┤ļéśĻ│Ā, ĻĘĖ ļ░śļÅäņ▓┤ļŖö Ēśäņ×¼Ļ╣īņ¦Ć Ļ░£ļ░£ļÉ£ ļīĆļČĆļČäņØś ņŚ┤ņĀä ņåīņ×¼ļź╝ ĒżĒĢ©ĒĢ£ļŗż.
ņ×¼ļŻīņØś ņĀäĻĖ░ ņĀäļÅäļÅä (Žā)ļŖö ņĀäĻĖ░ļź╝ ņ¢╝ļ¦łļéś ņל ņĀäļÅäĒĢśļŖöņ¦Ć ņĀĢļ¤ēĒÖöĒĢśĻ│Ā, ņ║Éļ”¼ņ¢┤ ļåŹļÅä (n), ņØ┤ļÅÖļÅä (m) ļ░Å ĻĖ░ļ│Ė ņĀäĒĢś ņāüņłś (e)ņØś Ļ│▒ņØ┤ļŗż (ņłśņŗØ 4). ņ║Éļ”¼ņ¢┤ ļåŹļÅäļŖö ņ×¼ļŻīņØś ņĀäļÅäļīĆ (conduction band)ņŚÉ ņ׳ļŖö ņĀäņ×É ļśÉļŖö Ļ░ĆņĀäņ×ÉļīĆ (valence band)ņŚÉ ņ׳ļŖö ņĀĢĻ│ĄņØś ļåŹļÅäņØ┤ļŗż. ņØ┤ļÅÖļÅäļŖö ņ║É ļ”¼ņ¢┤Ļ░Ć ņ×¼ļŻīļź╝ ĒåĄĒĢ┤ ņ¢╝ļ¦łļéś ņēĮĻ▓ī ņØ┤ļÅÖĒĢĀ ņłś ņ׳ļŖöņ¦Ćļź╝ ļéśĒāĆļéĖļŗż. ĻĖ░ļ│Ė ņĀäĒĢś ņāüņłś (e)ļŖö ļŗ©ņØ╝ ņĀäņ×É (1.6├Ś10-19 C)Ļ░Ć ņÜ┤ļ░śĒĢśļŖö ņĀäĒĢśļĪ£ ņĀĢņØśļÉ£ļŗż.
ņ×¼ļŻīņØś ņ┤Ø ņŚ┤ ņĀäļÅäļÅä (k)ļŖö ņŚ┤ ņĀäļÅäņ£©ņØä ņĀĢļ¤ēĒÖöĒĢśĻ│Ā, ņØ┤ļŖö Ļ▓®ņ×É ņŚ┤ ņĀäļÅäļÅä (k L)ņÖĆ ņĀäņ×É ņŚ┤ ņĀäļÅäļÅä (k e) ĻĖ░ņŚ¼ņØś ĒĢ®ņØ┤ļŗż (ņłśņŗØ 5). Ļ▓®ņ×É ņŚ┤ ņĀäļÅäļÅäļŖö ņ×¼ļŻīļź╝ ĒåĄĒĢ┤ ņĀäļŗ¼ļÉśļŖö Ļ▓®ņ×É ņ¦äļÅÖņŚÉņä£ ļ╣äļĪ»ļÉśĻ│Ā, ņØ┤ļź╝ ņØīĒ¢źņ¢æņ×É (phonon)ļØ╝Ļ│ĀļÅä ņØ╝ņ╗½ļŖöļŗż. ņĀäņ×É ņŚ┤ ņĀäļÅäļÅäļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņÖĆ ņ×¼ļŻī ļé┤ ņøÉņ×É Ļ░äņØś ņČ®ļÅīņŚÉņä£ ļ╣äļĪ»ļÉśļ»ĆļĪ£, Lorentz ņłś (L)ņÖĆ ņĀäĻĖ░ ņĀäļÅäļÅä (Žā)ņØś Ļ│▒ņŚÉ ļ╣äļĪĆĒĢ£ļŗż (ņłśņŗØ 6).
ņłśņŗØ 2ņŚÉņä£ ņĢī ņłś ņ׳ļō»ņØ┤, ļåÆņØĆ ZTļź╝ ļŗ¼ņä▒ĒĢśņŚ¼ ļåÆņØĆ ņŚ┤ ļ│ĆĒÖś ĒÜ©ņ£©ņØä ĻĄ¼ĒśäĒĢśļĀżļ®┤ ņĀäĻĖ░ ņĀäļÅäļÅä, ņĀ£ļ▓Ī Ļ│äņłśņØś ņ”ØĻ░Ć ļ░Å ņŚ┤ ņĀäļÅäļÅäņØś Ļ░ÉņåīĻ░Ć ļ░öļ×īņ¦üĒĢśļŗż. ĻĘĖļ¤¼ļéś ļåÆņØĆ ZTļź╝ ļŗ¼ņä▒ĒĢśļŖö Ļ▓āņØĆ ņØ┤ļōż 3Ļ░Ćņ¦Ć Ļ│äņłśĻ░Ć ņä£ļĪ£ Ļ┤ĆļĀ©ļÉśņ¢┤ ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ Ļ░äļŗ©ĒĢśņ¦Ć ņĢŖļŗż.
Fig 3ņØĆ ņŚ┤ņĀä ļ¼╝ņ¦ł ļé┤ļČĆņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ļåŹļÅäņØś ĒĢ©ņłśļĪ£ņä£ ņĀ£ļ▓Ī Ļ│äņłś, ņĀäĻĖ░ ļ░Å ņŚ┤ ņĀäļÅäļÅäļź╝ ļ│┤ņŚ¼ņżĆļŗż. ņĀäĻĖ░ ņĀäļÅäļÅäļŖö ņ║Éļ”¼ņ¢┤ ļ░ĆļÅäĻ░Ć ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ ņ”ØĻ░ĆĒĢśļŖö ļ░śļ®┤ ņĀ£ļ▓Ī Ļ│äņłśļŖö ņ║Éļ”¼ņ¢┤ ļåŹļÅäĻ░Ć ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ Ļ░ÉņåīĒĢ£ļŗż. ņĀ£ļ▓Ī Ļ│äņłśņÖĆ ņĀäĻĖ░ ņĀäļÅäļÅäņØś ņāüļ░śļÉ£ ņČöņäĖļĪ£ ņØĖĒĢ┤, ĒŖ╣ņĀĢ ņ║Éļ”¼ņ¢┤ ļåŹļÅäņŚÉņä£ ņČ£ļĀźņØĖņ×ÉņØś ņĄ£ļīōĻ░ÆņØ┤ ņĪ┤ņ×¼ĒĢśĻ▓ī ļÉ£ļŗż. ļśÉĒĢ£ ņ║Éļ”¼ņ¢┤ ļ░ĆļÅäĻ░Ć ņ”ØĻ░ĆĒĢ©ņŚÉ ļö░ļØ╝ ņŚ┤ ņĀäļÅäļÅäļÅä ņ”ØĻ░ĆĒĢśļŖöļŹ░, ņØ┤ļŖö ņŚ┤ ņĀäļÅäļÅäņŚÉ ļīĆĒĢ£ ņĀäņ×É ĻĖ░ņŚ¼ ļČäņØ┤ ļŹö ņ╗żņ¦ĆĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņØ┤ ļČäņäØņØä ĒåĄĒĢ┤ ZTļŖö ĒŖ╣ņĀĢ ņ║Éļ”¼ņ¢┤ ļåŹļÅäņŚÉņä£ ņĄ£ļīĆ Ļ░ÆļÅä Ļ░Ćņ¦ÉņØä ņČöļĪĀĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā3.
ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ļåŹļÅäļź╝ ĒåĄĒĢ£ ļ¼┤ņ░©ņøÉ ņä▒ļŖź ņ¦Ćņłś (ZT)ņØś ņĄ£ņĀüĒÖö. ĒĢ£ Ļ░Ćņ¦Ć ņŚ┤ņĀä ņ×¼ļŻī ļé┤ņŚÉņä£ ZTņØś ņĄ£ļīĆĒÖöļŖö ņŚ┤ ņĀäļÅäļÅä (╬║), ņĀ£ļ▓Ī Ļ│äņłś (S), ĻĘĖļ”¼Ļ│Ā ņĀäĻĖ░ ņĀäļÅäļÅä ņé¼ņØ┤ņØś ļīĆļ”Į Ļ┤ĆĻ│ä (tradeoff) ļź╝ ņĪ░ņ£©ĒĢ┤ņĢ╝ ņä▒ņĘ©ļÉĀ ņłś ņ׳ļŗż. Figure from Design and Preparation of High-Perfor-mance Bulk Thermoelectric Materials with Defect Structures and used with permission from Korean Ceramic Society18.

ZTņØś ņČöĻ░ĆņĀü Ļ░£ņäĀņØä ņ£äĒĢ┤ ņŚ¼ļ¤¼ ņŚ░ĻĄ¼Ļ░Ć ņŗ£Ē¢ēļÉśņŚłĻ│Ā, ņØ┤ ņĀäļץņØĆ Ļ▒░ņ╣ĀĻ▓ī 2Ļ░Ćņ¦Ć ĒØÉļ”äņ£╝ļĪ£ ļéśļłī ņłś ņ׳ļŗż. 1 ļ▓łņ¦ĖļŖö ņłśņŗØ 2ņØś ļČäļ¬©ņØĖ ņŚ┤ ņĀäļÅäļÅäļź╝ ļé«ņČöļŖö Ļ▓āņØ┤Ļ│Ā, 2ļ▓łņ¦ĖļŖö ņłśņŗØ 2ņØś ļČäņ×ÉņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņČ£ļĀźņØĖņ×É (power factor)ņØä ņĄ£ļīĆĒÖöĒĢśļŖö Ļ▓āņØ┤ļŗż. ņŚ┤ņĀä ņåīņ×¼ļź╝ ļ│ĄĒĢ® ņåīņ×¼ļĪ£ ļ¦īļō£ļŖö ņĀäļץņØĆ ņØīĒ¢źņ¢æņ×ÉĻ░Ć ņé░ļ×ĆļÉśļŖö ņןņåīļź╝ ļīĆļ¤ēņ£╝ļĪ£ ņāØņä▒ĒĢśņŚ¼ ņŚ┤ ņĀäļÅäļÅäļź╝ ļé«ņČöļŖö ļÅÖņŗ£ņŚÉ, ņČ£ļĀźņØĖņ×ÉņØä ņ”ØĻ░Ģņŗ£Ēé¼ Ļ░ĆļŖźņä▒ņØ┤ ņ׳ļŗżļŖö ņĀÉņŚÉņä£ ļ¦ÄņØ┤ ņŚ░ĻĄ¼ļÉśņŚłļŗż3-13. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ļ│ĄĒĢ® ņåīņ×¼ņŚÉņä£ ņČ£ļĀźņØĖņ×ÉņØä ņ”ØĻ░Ćņŗ£ĒéżļŖö ļ®öņ╗żļŗłņ”śļōżņŚÉ ļīĆĒĢ┤ ņ¦æņżæņĀüņ£╝ļĪ£ ĒāÉĻĄ¼ĒĢśĻ│Ā, ņØ┤ ļ®öņ╗żļŗłņ”śņØä ņŗżņĀ£ļĪ£ ĻĄ¼ĒśäĒĢśĻĖ░ ņ£äĒĢ┤ Ļ░¢ņČöņ¢┤ņĢ╝ ĒĢśļŖö ņĪ░Ļ▒┤Ļ│╝ ņøÉļ”¼, ĻĄ¼ĒśäļÉ£ ņśłņĀ£ņŚÉ ļīĆ ĒĢ┤ ņÜöņĢĮĒĢĀ Ļ▓āņØ┤ļŗż.
ļ│ĆņĪ░ ļÅäĒĢæ (modulation doping)
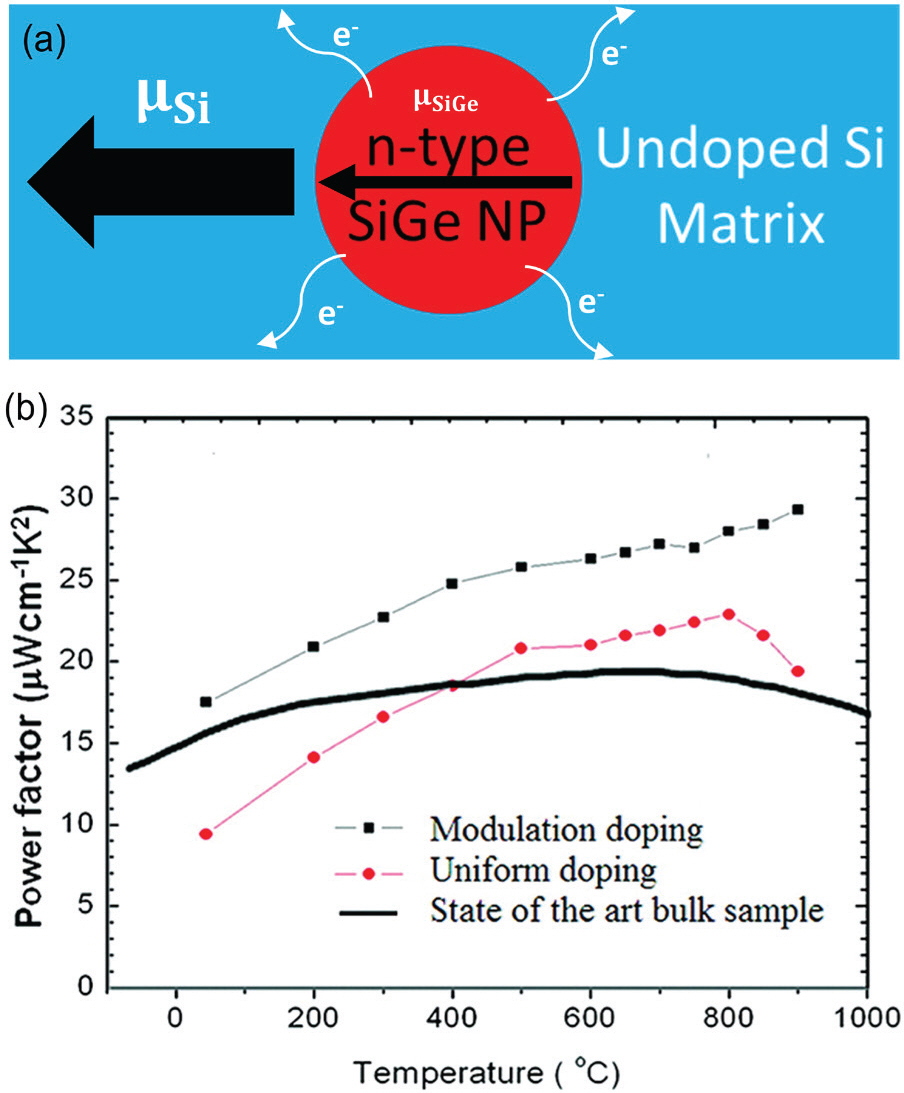
ļ│ĆņĪ░ ļÅäĒĢæņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļź╝ ļ¦ÄņØ┤ Ļ░Ćņ¦ä ņ×¼ļŻī AļĪ£ļČĆĒä░, ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ņĀüņØĆ ņØĖņĀæ ņ×¼ļŻī BļĪ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ĒÖĢņé░ļÉśļŖö ĒśäņāüņØä ņØ╝ņ╗½ļŖöļŗż. (Fig 4 (a)). ņØ┤ ņāüĒÖ®ņŚÉņä£ ņ×¼ļŻī B ļŖö ļČłņł£ļ¼╝ņØĖ ļÅäĒīÉĒŖĖ ņŚåņØ┤ļÅä ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņłśļ¤ēņØ┤ ļŖśņ¢┤ļéśļŖö ĒÜ©Ļ│╝ļź╝ ņ¢╗ĻĖ░ ļĢīļ¼ĖņŚÉ ļÅäĒĢæņ£╝ļĪ£ ļČäļźśļÉ£ļŗż. ņł£ņä£ ņāüņ£╝ļĪ£ļŖö (i) ļÅäĒĢæ ļÉ£ ļ░śļÅäņ▓┤ ņĖĄņŚÉņä£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņāØņä▒ ļ░Å (ii) ļŹö ļåÆņØĆ ņØ┤ļÅÖņä▒ņØä Ļ░¢ļŖö ņĀæņ┤ē ļÅäĒĢæ ļÉ£ ņĖĄņ£╝ļĪ£ņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņØ╝ļČĆ ņØ┤ļÅÖņØś ļæÉ Ļ░Ćņ¦Ć ĒöäļĪ£ņäĖņŖżļĪ£ ĻĄ¼ņä▒ļÉśĻ│Ā, ļö░ļØ╝ņä£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ņ×¼ļŻī AņŚÉņä£ ņ×¼ļŻī BļĪ£ ŌĆśļäśņ╣śļŖöŌĆÖ ĒśäņāüņØ┤ļØ╝Ļ│ĀļÅä ņä£ņłĀĒĢĀ ņłś ņ׳ļŗż. ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ ņĖĄņŚÉņä£ ļŹö ļåÆņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņØ┤ļÅÖļÅäĻ░Ć ņØ┤ļŻ©ņ¢┤ņ¦ĆļŖö ņØ┤ņ£ĀļŖö ļÅäĒÄĆĒŖĖ ņøÉņ×ÉņŚÉ ņØśĒĢ£ ņ║Éļ”¼ņ¢┤ ņé░ļ×ĆņØ┤ ņĀüĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņØ┤ ļ®öņ╗żļŗłņ”śņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļź╝ ņČöĻ░ĆļĪ£ ņāØņä▒ĒĢśņ¦Ć ņĢŖĻĖ░ ļĢīļ¼ĖņŚÉ, ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņĀäņ▓┤ ņØĖĻĄ¼ļŖö ļÅÖņØ╝ĒĢśĻ▓ī ņ£Āņ¦ĆļÉ£ļŗż. ĻĘĖļ¤¼ļéś ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ ņĖĄ (ņ×¼ļŻī B)ņØś ņØ╝ļČĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ņØ┤ņĀ£ ļŹö ļåÆņØĆ ņØ┤ļÅÖļÅäļź╝ Ļ░¢ĻĖ░ ļĢīļ¼ĖņŚÉ ņĀäĻĖ░ ņĀäļÅäļÅäĻ░Ć ņ”ØĻ░ĆĒĢ£ļŗż. ņØ┤ ņøÉļ”¼ļŖö GaAs / Al x Ga1-x As ņ┤łĻ▓®ņ×ÉņŚÉņä£ ņ▓śņØīņ£╝ļĪ£ ņ×ģņ”ØļÉśņŚłļŗż14. ņØ┤ Ļ░£ļģÉņØś ņ▓½ ļ▓łņ¦Ė ņĀüņÜ®ņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ļåÆņØĆ ņØ┤ļÅÖ ļÅäĻ░Ć ņä▒ļŖźĻ│╝ ņ¦üņĀæņĀüņ£╝ļĪ£ ņŚ░Ļ▓░ļÉ£ HEMT (high electron mobility transistor)ņśĆļŗż14.
Fig.┬Ā4.
ļéśļģĖ ņŖżņ╝ĆņØ╝ ļ│ĄĒĢ® ņ×¼ļŻīņŚÉņä£ ļ│ĆņĪ░ ļÅäĒĢæ ļ®öņ╗żļŗłņ”ś. (a) ļ│ĆņĪ░ ļÅäĒĢæņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņØ┤ļÅÖ ļ░®Ē¢źņØ┤ ņ×¼ļŻī Ļ░ä Ļ│äļ®┤Ļ│╝ ĒÅēĒ¢ēņØ╝ ļĢī ņŚ┤ņĀä ņä▒ļŖźņØä Ē¢źņāüņŗ£ĒéżļŖö ņøÉļ”¼Ļ░Ć ļÉĀ ņłś ņ׳ļŗż. ĒÜīņāēņØĆ ļÅäĒĢæļÉśņŚłņ£╝ļéś ņĀäĒĢś ņØ┤ļÅÖļÅäĻ░Ć ļé«ņØĆ ņ×¼ļŻīļź╝ ļéśĒāĆļé┤Ļ│Ā, Ļ▓ĆņØĆņāēņØĆ ļÅäĒĢæļÉśņ¦Ć ņĢŖņĢśņ£╝ļéś ņĀäĒĢś ņØ┤ļÅÖļÅäļŖö ļŹö Ēü░ ņ×¼ļŻīļź╝ ņØśļ»ĖĒĢ£ļŗż. ĒØ░ ņĀÉņ£╝ļĪ£ Ēæ£ņŗ£ĒĢ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ļÅäĒĢæņØ┤ ļ¦ÄņØ┤ ļÉ£ ņ×¼ļŻīļĪ£ļČĆĒä░ ļåŹļÅä ĻĄ¼ļ░░ ļĢīļ¼ĖņŚÉ ĒÖĢņé░ļÉśļŖö Ļ│╝ņĀĢņØä ļ│┤ņŚ¼ņżĆļŗż. (b) ļ│ĆņĪ░ ļÅäĒĢæņØĆ ĒÖöĒĢÖņĀüņ£╝ļĪ£ ļÅäĒĢæļÉ£ ņ×¼ļŻīļĪ£ļČĆĒä░ ļŹö ļåÆņØĆ ņØ┤ļÅÖļÅäļź╝ Ļ░Ćņ¦ä ņØĖņĀæ ņ×¼ļŻīļĪ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ŌĆ£ĒØśļ¤¼ ļäśņ╣śļŖöŌĆØ ĒśäņāüņØ┤ļŗż. ļÅäĒĢæ ļåŹļÅäņØś ņ░©ņØ┤ ņØ┤ņÖĖņŚÉļÅä, ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ĒØśļ¤¼ ļäśņ╣©ņØ┤ ņŚ┤ņŚŁĒĢÖņĀüņ£╝ļĪ£ ņĢłņĀĢĒĢ£ ĒśäņāüņØ┤ ļÉĀ ņłś ņ׳ļÅäļĪØ Ļ│äļ®┤ņŚÉņä£ ļ░┤ļō£ ļČłņŚ░ņåŹ (band offset)ņØ┤ ĻĄ¼ĒśäļÉśņ¢┤ņĢ╝ļ¦ī ļ╣äļĪ£ņåī ļ│ĆņĪ░ ļÅäĒĢæņØ┤ ĒÜ©Ļ│╝ņĀüņ£╝ļĪ£ ņØ╝ņ¢┤ļéĀ ņłś ņ׳ļŗż. ļŗżļźĖ ļ¦ÉļĪ£, ņØ┤ļŖö ļ░┤ļō£ ļČłņŚ░ņåŹņØś Ēü¼ĻĖ░ņÖĆ ļ░®Ē¢źņŚÉ ļö░ļØ╝, ņ¢╝ļ¦łļéś ļ¦ÄņØĆ ļČäņ£©ņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ĒØśļ¤¼ ļäśņ│Éņä£ ņØ┤ņŻ╝ĒĢĀ ņłś ņ׳ļŖöņ¦Ć Ļ▓░ņĀĢļÉ£ļŗż. ņØ┤ Ļ▓ĮņÜ░, Ļ│ĀļåŹļÅäļĪ£ ļÅäĒĢæ ļÉ£ Si x Ge1-x ļéśļģĖ ņ×ģņ×ÉņŚÉņä£ ņāØņä▒ļÉ£ ņĀäņ×ÉļŖö ņØĖņĀæĒĢ£ ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ Si ļ¦żĒŖĖļ”ŁņŖżļĪ£ ĒØśļ¤¼ļäśņ╣£ļŗż. ņØ┤ļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ļåŹļÅä ĻĄ¼ļ░░ņÖĆ ļ░┤ļō£ ļČłņŚ░ņåŹņØ┤ ļ¬©ļæÉ ņØ┤ ļ░®Ē¢źņ£╝ļĪ£ņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ĒÖĢņé░ņØä ņ¦Ćņ¦ĆĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. Figure (a) from Quantitative analyses of enhanced thermoelectric properties of modulation-doped PEDOT:PSS/undoped Si (001) nanoscale heterostructures15. Reproduced by permission of the Royal Society of Chemistry. Figure (b) from Enhancement of thermoelectric properties by modulation-doping in silicon germanium alloy nanocompos-ites and used with permission from the American Chemical Society6.

ļ│ĆņĪ░ ļÅäĒĢæņØ┤ ĒÖ£ļ░£ĒĢśĻ▓ī ņŗżĒśäļÉśņ¢┤ ļ¦ÄņØĆ ņ¢æņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ņ×¼ļŻī AņŚÉņä£ ņ×¼ļŻī BļĪ£ ŌĆśļ¦ÄņØ┤ ļäśņ╣śĻĖ░ŌĆÖ ņ£äĒĢ┤ņä£ļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņØ┤ļÅÖņØ┤ ņŚ┤ņŚŁĒĢÖņĀüņ£╝ļĪ£ ļé┤ļ”¼ļ¦ē (ņ×Éļ░£ņĀüņØĖ ļ░£ņŚ┤ļ░śņØæ)ņØ┤ņ¢┤ņĢ╝ ĒĢśĻ│Ā, ņØ┤ļŖö ņ×¼ļŻī AņÖĆ ņ×¼ļŻī BņØś Ļ│äļ®┤ņŚÉņä£ņØś ļ░┤ļō£ ļČłņŚ░ņåŹ (band offset)ņ£╝ļĪ£ Ļ▓░ņĀĢļÉ£ļŗż. ļ░┤ļō£ ļČłņŚ░ņåŹņØĆ ņä£ļĪ£ ļŗżļźĖ ļæÉ ņ×¼ļŻīņØś Ļ▓ĮĻ│äļ®┤ņŚÉņä£, ņĀäļÅäļīĆ ļśÉļŖö Ļ░ĆņĀäņ×ÉļīĆĻ░Ć ļ│┤ņØ┤ļŖö ļČłņŚ░ņåŹ ņŚÉļäłņ¦ĆņØś Ēü¼ĻĖ░ņØ┤ļŗż. ļ░┤ļō£ ļČłņŚ░ņåŹņØ┤ ņŚ┤ņŚŁĒĢÖņĀüņ£╝ļĪ£ ņśżļź┤ļ¦ēņØ┤ļØ╝ļ®┤ (ļ╣äņ×Éļ░£ņĀü ĒØĪņŚ┤ļ░śņØæ) ņ×¼ļŻī AņŚÉņä£ ņØĖņĀæĒĢ£ ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ ļ░śļÅäņ▓┤ ņ×¼ļŻī BļĪ£ņØś ĒÖĢņé░ņØ┤ Ēü¼Ļ▓ī ņ¢ĄņĀ£ļÉ£ļŗż. ļ░śļīĆļĪ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņ×¼ļČäļ░░Ļ░Ć ņŚ┤ņŚŁĒĢÖņĀüņ£╝ļĪ£ ņ£Āļ”¼ĒĢĀ ļĢī (ļé┤ļ”¼ļ¦ē), ļīĆļČĆļČäņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļŖö ņØĖņĀæ ņ×¼ļŻī B ļĪ£ņØś ņ×¼ļ░░ņ╣śļź╝ ņäĀĒśĖĒĢ£ļŗż6, 7, 15, 16.
Fig 4 (b)ļŖö nĒśĢņ£╝ļĪ£ ļ¦ÄņØ┤ ļÅäĒĢæļÉ£ Si x Ge1-x ļéśļģĖ ņ×ģņ×Éļź╝ ĒĢ©ņ£ĀĒĢśļŖö ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ Si ļ¦żĒŖĖļ”ŁņŖżņŚÉņä£ ņØ╝ņ¢┤ļéśļŖö ļ│ĆņĪ░ ļÅäĒĢæ Ļ│╝ņĀĢņØä ļ│┤ņŚ¼ņżĆļŗż. ņØ┤ Ļ▓ĮņÜ░, ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļź╝ ņĀ£Ļ│ĄĒĢśļŖö ņ×¼ļŻī A (ļ¦ÄņØ┤ ļÅäĒĢæļÉ£ n ĒśĢ Si x Ge1-x ļéśļģĖ ņ×ģņ×É)ņØś ņĀäļÅäļīĆļŖö ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆSiņØś ņĀäļÅäļīĆļ│┤ļŗż ņŚÉļäłņ¦ĆņĀüņ£╝ļĪ£ ļåÆĻ▓ī ņ£äņ╣śĒĢ£ļŗż. ņØ┤ļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ĒÖĢņé░ņØ┤ ņŚ┤ņŚŁĒĢÖņĀüņ£╝ļĪ£ ņ£Āļ”¼ĒĢśļÅäļĪØ ļ░┤ļō£Ļ░Ć ņĀĢļĀ¼ĒĢśļÅäļĪØ ņ×¼ļŻīļź╝ ņäĀĒāØĒ¢łĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ļö░ļØ╝ņä£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņ×¼ļ░░ņŚ┤ņØ┤ ņŚ┤ņŚŁĒĢÖņĀü ļé┤ļ”¼ļ¦ē ļ░śņØæ (ļ░£ņŚ┤ļ░śņØæ)ņ×äņØä ņØśļ»ĖĒĢśĻ│Ā, ņ×Éļ░£ņĀüņ£╝ļĪ£ ļ│ĆņĪ░ ļÅäĒĢæņØ┤ ļ░£ņāØĒĢ©ņØä ņØśļ»ĖĒĢ£ļŗż.
ņØ┤ Ļ▓ĮņÜ░, ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļź╝ ņĀ£Ļ│ĄĒĢśļŖö ņ×¼ļŻī AņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö Si x Ge1-x ļéśļģĖ ņ×ģņ×ÉļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ ņĀäņ×ÉņØś ņé░ļ×Ć ņżæņŗ¼ņ£╝ļĪ£ Ļ░äņŻ╝ļÉ£ļŗż6,7. ņØ┤ ĒÜ©Ļ│╝Ļ░Ć ņÜ░ņäĖĒĢśļŗżļ®┤ ļ│ĆņĪ░ ļÅäĒĢæņØ┤ ņØ╝ņ¢┤ļé¼ņØīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ņĀäĻĖ░ ņĀäļÅäļÅäņØś Ē¢źņāüņØĆ ņØ╝ņ¢┤ļéśņ¦Ć ņĢŖņØä ņłś ņ׳ļŗż. ņØĖņÜ®ļÉ£ ĒĢ┤ļŗ╣ ļģ╝ļ¼ĖņŚÉņä£ļŖö6,7 Si x Ge1-x ļéśļģĖ ņ×ģņ×ÉņØś Ēü¼ĻĖ░Ļ░Ć (~ 20 nm) ņĀäņ×ÉņØś ĒÅēĻĘĀ ņ×Éņ£Ā Ļ▓ĮļĪ£ (1 nm ŌĆō 20 nm)ļ│┤ļŗż Ēü¼ĻĖ░ ļĢīļ¼ĖņŚÉ ņĀäĻĖ░ ņĀäļÅäļÅäņØś Ē¢źņāüņØ┤ Ļ░ĆļŖźĒĢśņśĆļŗż. ņ”ē, ĒĢ┤ļŗ╣ ļ│ĄĒĢ® ņŚ┤ņĀä ņ×¼ļŻīņŚÉņä£ ļīĆļČĆļČäņØś ņĀäņ×ÉļŖö ļéśļģĖ ņ×ģņ×ÉņŚÉ ņØśĒĢ┤ ņé░ļ×ĆļÉśĻĖ░ļ│┤ļŗżļŖö ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ Si ļ¦żĒŖĖļ”ŁņŖż ĻĘĖ ņ×Éņ▓┤ļĪ£ ņØĖĒĢ┤ ņé░ļ×ĆļÉ£ļŗż. ļ│ĆņĪ░ ļÅäĒĢæņØä ņØ╝ņ£╝ĒéżļŖö ļ│ĆņĪ░ ļÅäĒīÉĒŖĖĻ░Ć ļéśļģĖ ņ×ģņ×ÉņØ╝ ļĢī, ļéśļģĖ ņ×ģņ×ÉņØś Ēü¼ĻĖ░ļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ĒÅēĻĘĀ ņ×Éņ£Ā Ļ▓ĮļĪ£ļ│┤ļŗż ņ×æņĢäņĢ╝ ĒĢ£ļŗżļŖö ĻĄÉĒøłņØ┤ ļÅäņČ£ļÉ£ļŗż. ņŚ┤ņĀä ņä▒ļŖźņŚÉ ņ׳ņ¢┤ņä£, ļ│ĆņĪ░ ļÅäĒĢæņØś Ļ▓░Ļ│╝ļĪ£ ņĀ£ļ▓Ī Ļ│äņłśļź╝ ĒؼņāØĒĢśņ¦Ć ņĢŖĻ│ĀļÅä ņĀäĻĖ░ ņĀäļÅäļÅäĻ░Ć Ē¢źņāüļÉśņŚłĻ│Ā, ņØ┤ļŖö ņČ£ļĀźņØĖņ×ÉņØś ņ”ØĻ░Ģņ£╝ļĪ£ ņØ┤ņ¢┤ņĪīļŗż (Fig 5 (b)). ņØ┤ ņĀäļץņØś ļśÉ ļŗżļźĖ ņןņĀÉņØĆ Si x Ge1-x ļéśļģĖ ņ×ģņ×ÉĻ░Ć ņØīĒ¢źņ¢æņ×É ļśÉĒĢ£ ņé░ļ×Ćņŗ£ĒéżĻ│Ā, ņØ┤ļĪ£ ņØĖĒĢ┤ ņŚ┤ņĀäļÅäļź╝ ņ¢ĄņĀ£ĒĢ£ļŗżļŖö ņĀÉņØ┤ļŗż6,7. ņØīĒ¢źņ¢æņ×ÉņØś ĒÅēĻĘĀ ņ×Éņ£Ā Ļ▓ĮļĪ£ (ņłś m m Ļ░Ćļ¤ē)Ļ░Ć ņĀäņ×ÉņØś ĻĘĖĻ▓āņŚÉ ļ╣äĒĢ┤ Ēø©ņö¼ ĻĖĖĻĖ░ ļĢīļ¼ĖņŚÉ, ņłśņŗŁ nmļ¦łļŗż ņé░ļ×Ć ņżæņŗ¼ņØĖ ļéśļģĖ ņ×ģņ×ÉĻ░Ć ļČäĒżĒĢśļŖö ņāüĒÖ®ņØĆ ņĀäņ×ÉņŚÉ ļ╣äĒĢ┤ ņØīĒ¢źņ¢æņ×ÉņØś ņé░ļ×ĆņØ┤ Ēø©ņö¼ ņŗ¼Ļ░üĒĢ┤ņ¦ÉņØä ņØśļ»ĖĒĢ£ļŗż.4,5
Fig.┬Ā5.
(a) ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ Si ļ¦żĒŖĖļ”ŁņŖżņÖĆ nĒśĢ Si x Ge1-x ļéśļģĖ ņ×ģņ×ÉņØś ļ│ĄĒĢ® ņ×¼ļŻīņŚÉņä£ ļ│ĆņĪ░ ļÅäĒĢæ. nĒśĢ ļÅäĒĢæļÉ£ Si x Ge1-x ļéśļģĖ ņ×ģņ×ÉļĪ£ļČĆĒä░ ĒØśļ¤¼ļäśņ╣£ ņĀäņ×ÉļŖö ļåÆņØĆ ņØ┤ļÅÖļÅäļź╝ Ļ░Ćņ¦ä Si ļ¦żĒŖĖļ”ŁņŖżļź╝ ĒåĄĒĢ┤ ļŹö ļ╣Āļź┤Ļ▓ī ņØ┤ļÅÖĒĢśņŚ¼ ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ Ļ░£ņäĀĒĢ£ļŗż. (b) ĒĢ┤ļŗ╣ ļ│ĄĒĢ® ņ×¼ļŻīļŖö ĻĘĀņØ╝ĒĢśĻ▓ī ļÅäĒĢæļÉ£ SiņŚÉ ļ╣äĒĢ┤ņä£ ņČ£ļĀźņØĖņ×ÉņØ┤ Ļ░£ņäĀļÉśņŚłņØīņØä ļ│╝ ņłś ņ׳Ļ│Ā, ņØ┤ļ¤¼ĒĢ£ Ē¢źņāüņØĆ ņŻ╝ļĪ£ ņĀ£ļ▓Ī Ļ│äņłśņØś ņåÉĒĢ┤ ņŚåņØ┤ ņĀäĻĖ░ ņĀäļÅäļÅäĻ░Ć ņ”ØĻ░ĆĒ¢łĻĖ░ ļĢīļ¼Ėņ£╝ļĪ£ ļČäņäØļÉ£ļŗż. Figure (b) from Power factor enhancement by modulation doping in bulk nanocomposites and used with permission from the American Chemical Society7.
ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć (energy-dependent charge carrier scattering)
ņØ┤ ļ®öņ╗żļŗłņ”śņØĆ ņä£ļĪ£ ļŗżļźĖ ļæÉ ņ×¼ļŻī ņé¼ņØ┤ņØś Ļ│äļ®┤ņŚÉņä£ ļ░£ņāØĒĢśļŖö ļ░┤ļō£ ļČłņŚ░ņåŹ (band offset)ņØ┤ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņŚÉļäłņ¦Ć ņןļ▓Įņ£╝ļĪ£ ņ×æņÜ®ĒĢĀ ļĢī, ņŚÉļäłņ¦ĆĻ░Ć ļé«ņØĆ ņ║Éļ”¼ņ¢┤Ļ░Ć ņŚÉļäłņ¦ĆĻ░Ć ļåÆņØĆ ņ║Éļ”¼ņ¢┤ņŚÉ ļ╣äĒĢ┤ ļŹö ļåÆņØĆ ĒÖĢļźĀļĪ£ ņé░ļ×ĆļÉ©ņØä ņØ┤ņÜ®ĒĢ£ļŗż. ĻĘĖļź╝ ĒåĄĒĢ┤ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņØ┤ļÅÖļÅäņÖĆ ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ ņØ╝ļČĆ ĒؼņāØĒĢ©ņ£╝ļĪ£ņŹ©, ņĀ£ļ▓Ī Ļ│äņłśļź╝ ĒéżņÜ░Ļ│Ā ņóģĻĄŁņŚÉļŖö ņČ£ļĀźņØĖņ×ÉņØä ņ”ØĻ░Ģņŗ£ĒéżļŖö ņĀäļץņØ┤ļŗż. ņŚ┤ņŚŁĒĢÖņĀüņØĖ Ļ┤ĆņĀÉņŚÉņä£ ņĀ£ļ▓Ī Ļ│äņłśļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ 1Ļ░£Ļ░Ć ņłśņåĪĒĢśļŖö ĒÅēĻĘĀ ņŚöĒŖĖļĪ£Ēö╝ņØ┤ļŗż2. ļö░ļØ╝ņä£ ņØ┤ ņĀäļץņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ 1Ļ░£ ļŗ╣ ņłśņåĪĒĢśļŖö ĒÅēĻĘĀ ņŚöĒŖĖļĪ£Ēö╝ņØś Ēü¼ĻĖ░ļź╝ ļåÆĻ▓ī ļ¦īļōżņ¢┤, ņĀ£ļ▓Ī Ļ│äņłśļź╝ ņś¼ļ”¼ļŖö ļ░®ņŗØņØ┤ļŗż. ņ×¼ļŻī AņÖĆ ņ×¼ļŻī BĻ░Ć ņØ╝ņĀĢĒĢ£ ļæÉĻ╗śļź╝ Ļ░Ćņ¦ĆĻ│Ā ļ░śļ│ĄņĀüņ£╝ļĪ£ ņ”Øņ░®ļÉśņ¢┤ ņ׳ļŖö ņ┤łĻ▓®ņ×É (superlattice)13 ļśÉļŖö ļ¦żĒŖĖļ”ŁņŖżņŚÉ ļ¼╗Ē×ī ļéśļģĖ ņ×ģņ×É10, 11ļŖö ņØ┤ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć ļ®öņ╗żļŗłņ”śņØä ņØ╝ņ£╝ĒéżĻĖ░ ņ£äĒĢ┤ ņäĀĒśĖļÉśļŖö ļ│ĄĒĢ® ņåīņ×¼ ĻĄ¼ņä▒ ļ░®ņŗØņØ┤ļŗż. ņØ┤ļź╝ ĒåĄĒĢ┤ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņé░ļ×ĆņØ┤ ņØ╝ņ¢┤ļéśļŖö Ļ│äļ®┤ņŚÉ ņØśĒĢ£ ĒÜ©Ļ│╝ļź╝ ņØśļÅäņĀüņ£╝ļĪ£ ļŖśņØ┤Ļ▒░ļéś ņżäņØ┤ļŖö ĒåĄņĀ£Ļ░Ć Ļ░ĆļŖźĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż (Fig 6 (a)).
Fig.┬Ā6.
(a) ņ┤łĻ▓®ņ×É (superlattice)ļź╝ ĒżĒĢ©ĒĢ£ ļéśļģĖņŖżņ╝ĆņØ╝ ļ│ĄĒĢ® ņ×¼ļŻīņŚÉņä£ Ļ│äļ®┤ ņןļ▓Į ņŚÉļäłņ¦ĆņŚÉ ļö░ļźĖ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć ļ®öņ╗żļŗłņ”ś. ņØ┤ ļ®öņ╗żļŗłņ”śņØĆ ļéśļģĖ ņ×ģņ×ÉļōżĻ│╝ ĻĘĖļź╝ Ļ░Éņŗ╝ ļ¦żĒŖĖļ”ŁņŖż, Ēś╣ņØĆ ņ┤łĻ▓®ņ×ÉņŚÉņä£ ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ ĒؼņāØĒĢśļŖö ļīōĻ░ĆļĪ£ ņĀ£ļ▓Ī Ļ│äņłśļź╝ Ē¢źņāüņŗ£Ēé¼ ņłś ņ׳ļŗż. ņØ┤ ļ®öņ╗żļŗłņ”śņØä ņØ╝ņ£╝ĒéżļĀżļ®┤ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņÖĆ ņŚ┤ņØś ņĀäļŗ¼ņØĆ ņ×¼ļŻī ņé¼ņØ┤ņØś ŌĆ£Ļ│äļ®┤ņØä ļܽļŖö ļ░®Ē¢źŌĆØņ£╝ļĪ£ ņØ╝ņ¢┤ļéśņĢ╝ ĒĢ£ļŗż. ĒÜīņāēĻ│╝ Ļ▓ĆņØĆņāēņØĆ Ļ░üĻ░ü ņĀäļÅäņä▒ ņ×¼ļŻī AņÖĆ ļŗżļźĖ ņóģļźśņØś ņĀäļÅäņä▒ ņ×¼ļŻī Bļź╝ ļéśĒāĆļé┤Ļ│Ā, ĒØ░ ņĀÉņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļź╝ ļ¬©ņé¼ĒĢ£ļŗż. Ļ│äļ®┤ņŚÉņä£ ņØ╝ņ¢┤ļéśļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņé░ļ×ĆņØ┤ ļ¼śņé¼ļÉśņ¢┤ ņ׳ļŗż. (b) 2Ļ░Ćņ¦Ć ņ×¼ļŻīĻ░Ć ņ┤łĻ▓®ņ×ÉņØś ĒśĢĒā£ļĪ£ ļ│ĄĒĢ® ņ×¼ļŻīļź╝ ĒśĢņä▒ĒĢĀ ļĢī Ļ░ĆņĀäņ×ÉļīĆ (conduction band). 2Ļ░Ćņ¦Ć ņ×¼ļŻī ņżæ ĒĢ£ Ļ░Ćņ¦ĆļŖö ņ¢ćņØĆ ļæÉĻ╗śļĪ£ ņØĖĒĢ┤ ņ¢æņ×É ĻĄ¼ņåŹ ĒÜ©Ļ│╝ (quantum confinement effect)ļź╝ Ļ░Ćņ¦äļŗżĻ│Ā ņāüņĀĢļÉśņ¢┤, ņ¢æņ×É ņÜ░ļ¼╝ (quantum well)ņØś ĒśĢĒā£ļĪ£ Ēæ£ĒśäļÉśņŚłļŗż. Ļ░ü ņÜ░ļ¼╝ņØś ņןļ▓Į ļåÆņØ┤ņÖĆ ĒÄśļź┤ļ»Ė ļĀłļ▓©ņØĆ Ļ░üĻ░ü E bņÖĆ E fļĪ£ Ēæ£ņŗ£ļÉśņŚłļŗż. ņś©ļÅä (T HņÖĆ T L)ņØś ņ░©ņØ┤ ļĢīļ¼ĖņŚÉ ņĀäņ×ÉņØś ņŚÉļäłņ¦Ć ļĀłļ▓©ļÅä ĻĘĀļō▒ĒĢśĻ▓ī ĒÅēĒ¢ē ņØ┤ļÅÖĒĢśņśĆļŗż. (c) ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ ļ¬©ļōĀ ņĀäņ×ÉņØś ņÜ┤ļÅÖ ņŚÉļäłņ¦Ć ļČäĒżļŖö ņÜ┤ļÅÖļ¤ē Ļ│ĄĻ░ä (k Ļ│ĄĻ░ä)ņ£╝ļĪ£ Ēæ£ņŗ£ļÉĀ ņłś ņ׳ļŗż. Ļ│äļ®┤ ņןļ▓ĮņØś ļåÆņØ┤ E bļ│┤ļŗż ļŹö Ēü░ ņÜ┤ļÅÖ ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ä ņĀäņ×Éļ¦īņØ┤ Ļ│äļ®┤ņØä ŌĆ£ļø░ņ¢┤ļäśņ¢┤ŌĆØ ņĀäļŗ¼ļÉĀ ņłś ņ׳Ļ│Ā (V1Ļ│╝ V2ņŚÉ ĒĢ┤ļŗ╣), ĻĘĖļĀćņ¦Ć ņĢŖņ£╝ļ®┤ ņé░ļ×ĆļÉ£ļŗż. (d) ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ Ļ│äļ®┤ņŚÉņä£ ņŚÉļäłņ¦Ć ņןļ▓ĮņØ┤ ņ׳ņØä ļĢīņØś Žā(E) ĒĢ©ņłś. Žā(E) ĒĢ©ņłśļŖö ĒĢ┤ļŗ╣ ņŚÉļäłņ¦Ć Eļź╝ Ļ░Ćņ¦ä ņĀäņ×É ļČäņ£©ļĪ£ ņØĖĒĢ£ ņĀäĻĖ░ ņĀäļÅäļÅäņØ┤Ļ│Ā, ĒÄśļź┤ļ»Ė ļĀłļ▓©ņŚÉņä£ņØś Žā(E) ĒĢ©ņłśņØś ĻĖ░ņÜĖĻĖ░Ļ░Ć ņĀ£ļ▓Ī Ļ│äņłśņŚÉ ļ╣äļĪĆĒĢ£ļŗż. (e) ņןļ▓Į ņŚÉļäłņ¦ĆņŚÉ ņØśĒĢ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć ļ®öņ╗żļŗłņ”ś ņŗ£ ņśłņāüļÉśļŖö ZTņØś Ļ░£ņäĀ ņĀĢļÅä. Figure (a) from Quantitative analyses of enhanced thermoelectric properties of modulation-doped PEDOT:PSS/undoped Si (001) nanoscale heterostructures15. Reproduced by permission of the Royal Society of Chemistry. Figure (b) ŌĆō (e) from Improved thermo-electric power factor in metal-based superlattices and used with permission from the American Physical Society13.
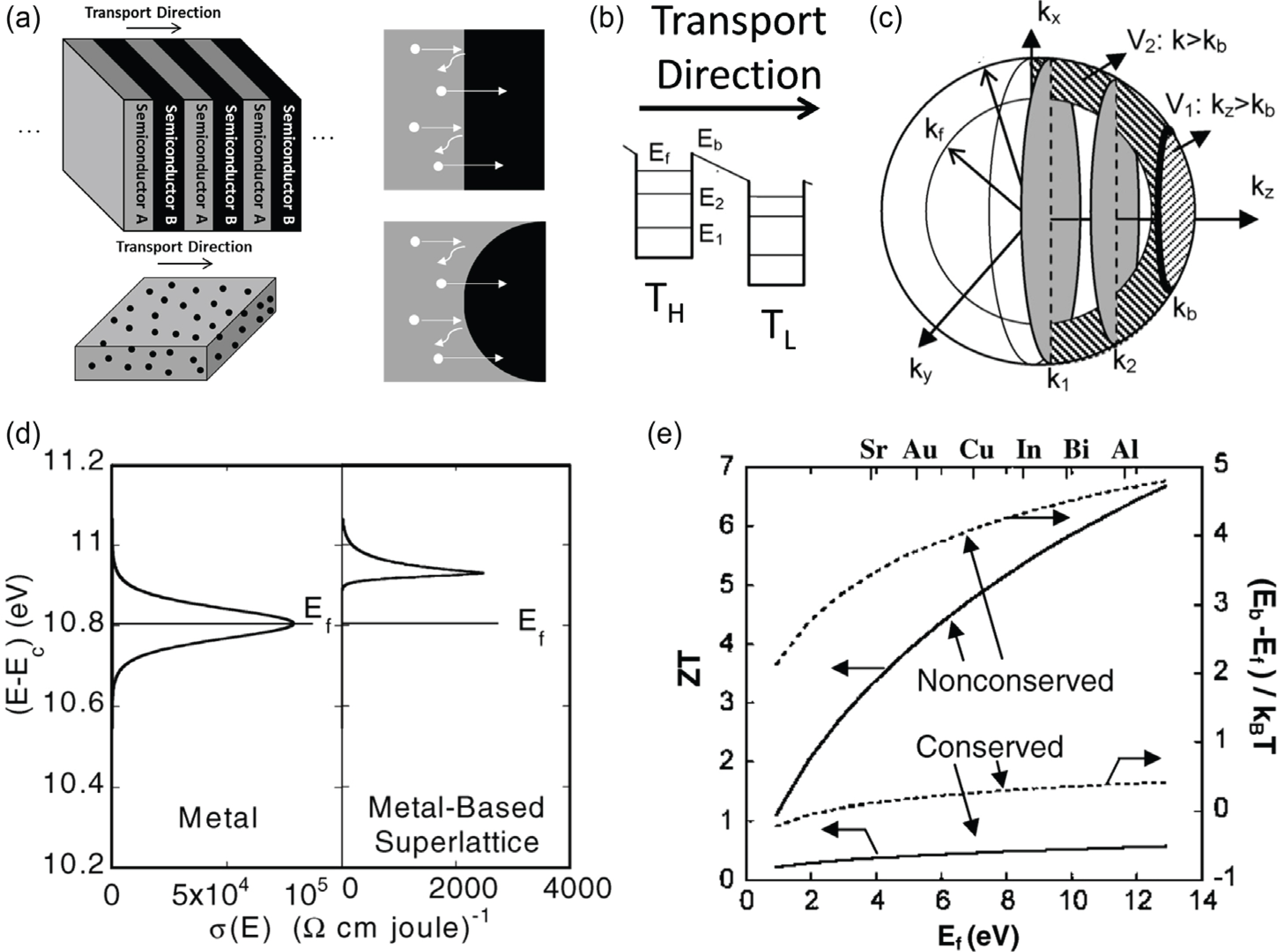
Fig 6 (b)ļŖö ņØ┤ļ¤¼ĒĢ£ ļ│ĄĒĢ® ņŚ┤ņĀä ņ×¼ļŻīņŚÉ ņś©ļÅä ĻĄ¼ļ░░Ļ░Ć Ļ░ĆĒĢ┤ņĪīņØä ļĢīņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņŚÉļäłņ¦Ćļź╝ ļ│┤ņŚ¼ņżĆļŗż. ņś©ļÅä ĻĄ¼ļ░░ ļĢīļ¼ĖņŚÉ ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ņØś ņĀäņ×ÉļŖö ņ£äņ╣ś ļ│äļĪ£ ļŗżļźĖ ĒÅēĻĘĀ ņÜ┤ļÅÖ ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ĆĻ▓ī ļÉ©ņØ┤ ļéśĒāĆļéśņ׳ļŗż. ļśÉĒĢ£, ņ¢æņ×É ņÜ░ļ¼╝ (quantum well)ņØ┤ Ļ░ĆņĀĢļÉśņ¢┤ ņ׳ļŖöļŹ░, ņØ┤ļŖö ņ┤łĻ▓®ņ×Éļź╝ ņØ┤ļŻ©ļŖö ļ│ĄĒĢ® ņ×¼ļŻī ņżæ 1Ļ░£ņØś ļæÉĻ╗śĻ░Ć ņ¢æņ×É ĻĄ¼ņåŹ (quantum confinement effect) ĒÜ©Ļ│╝ļź╝ ņØ╝ņ£╝Ēé¼ ņĀĢļÅäļĪ£ ņ¢ćņØĆ ņāüĒÖ®ņØä ņāüņĀĢĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņĀäņ×ÉĻ░Ć ļ│ĄĒĢ® ņåīņ×¼ļź╝ ĻĄ¼ņä▒ĒĢśļŖö ņ×¼ļŻī AņÖĆ ņ×¼ļŻī BņØś Ļ│äļ®┤ņØä Ļ▒┤ļäłņä£ ņØ┤ļÅÖĒĢśļ®┤, ļĪ£ Ēæ£ĒśäļÉśļŖö ņןļ▓Įļ│┤ļŗż ņ×æņØĆ ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ä ņĀäņ×ÉļōżņØĆ ļŹö ņØ┤ņāü ļéśņĢäĻ░ł ņłś ņŚåļŗż. ņśżļĪ£ņ¦Ć ņןļ▓Į ļåÆņØ┤ļ│┤ļŗż ļŹö ļåÆņØĆ ņÜ┤ļÅÖ ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ä ņĀäņ×Éļōż (E’╝× E b)ļ¦īņØ┤ Ļ│äņåŹ ņØ┤ļÅÖĒĢĀ ņłś ņ׳ļŗż. ņØ┤ Ļ▓ĮņÜ░ ņןļ▓ĮņØä ļܽļŖö Ēä░ļäÉļ¦ü ĒÜ©Ļ│╝ļŖö ļ¼┤ņŗ£ļÉ£ļŗż.
ņØ┤ļź╝ ņŗ£Ļ░üņĀüņ£╝ļĪ£ ļéśĒāĆļéĖ Ļ▓āņØ┤ Fig 6 (c)ņØ┤Ļ│Ā, ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ņØś ņĀäņ×É ņżæ ņ¢╝ļ¦īĒü╝ņØ┤ Ļ│äļ®┤ņØś ņŚÉļäłņ¦Ć ņןļ▓ĮņØä ĒåĄĻ│╝ĒĢśļŖöņ¦Ćļź╝ ļ│┤ņŚ¼ņżĆļŗż. ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ ņĀäņ▓┤ ņĀäņ×ÉņØś ņŚÉļäłņ¦ĆļŖö ņÜ┤ļÅÖļ¤ē Ļ│ĄĻ░ä (k Ļ│ĄĻ░ä)ņŚÉ Ēæ£ņŗ£ļÉśņŚłļŗż. ļō▒ļ░®ņä▒ ņ×Éņ£Ā ņĀäņ×ÉĻ░Ć Ļ░ĆņĀĢļÉśĻĖ░ ļĢīļ¼ĖņŚÉ ņÜ┤ļÅÖ ņŚÉļäłņ¦ĆļŖö ņÜ┤ļÅÖļ¤ē Ļ│ĄĻ░äņŚÉņä£ ĻĄ¼ĒśĢņØś ļČäĒżļź╝ ļØĀĻ│Ā, ņØ┤ļŖö ĻĖłņåŹ (ĒÄśļź┤ļ»Ė Ļ░ĆņŖż)ņØś ņĀäĒśĢņĀüņØĖ ĒŖ╣ņä▒ņØä ļ░śņśüĒĢ£ļŗż. Ļ│äļ®┤ņŚÉņä£ņØś ņŚÉļäłņ¦Ć ņןļ▓ĮņØä ļܽĻ│Ā ņĀäļŗ¼ ļÉĀ ņłś ņ׳ļŖö ŌĆśņŚ¼Ļ│╝ŌĆÖņØś ĻĖ░ņżĆ ņÜ┤ļÅÖ ņŚÉļäłņ¦ĆļŖö ļŗżņØī Ļ│ĄņŗØņŚÉ ņØśĒĢ┤ ņÜ┤ļÅÖļ¤ēĻ│╝ Ļ┤ĆļĀ©ļÉ£ļŗż.
ņŚ¼ĻĖ░ņä£ E, ŌäÅ, k, m e ŌłŚļŖö Ļ░üĻ░ü ņĀäņ×ÉņØś ņÜ┤ļÅÖ ņŚÉļäłņ¦Ć, Ēöīļ×æĒü¼ ņāüņłś, ņĀäņ×ÉņØś ņÜ┤ļÅÖļ¤ē ļ░Å ņĀäņ×ÉņØś ņ£ĀĒÜ© ņ¦łļ¤ēņØä ļéśĒāĆļéĖļŗż. ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ņŚÉ ņ׳ļŖö ņĀäņ▓┤ ņĀäņ×É ņżæ Ļ│äļ®┤ņØś ņŚÉļäłņ¦Ć ņןļ▓ĮņØä ļܽĻ│Ā ņĀäļŗ¼ļÉĀ ņłśņ׳ļŖö ņĀäņ×ÉņØś ļČäņ£©ņØĆ, Ļ▓░ĻĄŁ Ļ│äļ®┤ņŚÉ ņ׳ļŖö ņŚÉļäłņ¦Ć ņןļ▓ĮņØä ŌĆ£ļܽņØä ņłś ņ׳ļŖÉļāÉŌĆØņØś ņŚ¼ļČĆĻ░Ć ņżæņÜöĒĢśļŗż. ņØ┤ļŖö Ļ│äļ®┤ņØä ļܽļŖö ļ░®Ē¢źņØĖ zļ░®Ē¢źņØś ņÜ┤ļÅÖļ¤ē (k z)ņ£╝ļĪ£ ņØĖĒĢ£ ņÜ┤ļÅÖ ņŚÉļäłņ¦ĆĻ░Ć Ļ│äļ®┤ņŚÉņä£ņØś ņŚÉļäłņ¦Ć ņןļ▓Įļ│┤ļŗż ņ╗żņĢ╝ ĒĢ©ņØä ņØśļ»ĖĒĢ£ļŗż (( h 2 k z 2 2 m e ŌłŚ ŌĆē > ŌĆē E b )
Ļ│äļ®┤ ņןļ▓Į ņŚÉļäłņ¦ĆņŚÉ ņØśĒĢ£ ņĀäņ×ÉņØś ņäĀĒāØņĀü ņé░ļ×Ć ļĢīļ¼ĖņŚÉ, ĻĖ░ņĪ┤ ŌĆ£ņ×Éņ£Ā ņĀäņ×ÉŌĆØ ņżæ ņןļ▓ĮņØä ĻĘ╣ļ│ĄĒĢĀ ņłś ņŚåļŖö ļČäņ£©ņØĆ ļŹö ņØ┤ņāü ņ×Éņ£Ā ņĀäņ×ÉĻ░Ć ņĢäļŗłĻ▓ī ļÉśņ¢┤ļ▓äļ”░ļŗż. ņ”ē, ņĀäļÅäņŚÉ ĒÖ£ņÜ® ļÉśļŖö ŌĆ£ņ×Éņ£ĀŌĆØ ņĀäņ×ÉņØś ļåŹļÅäĻ░Ć Ļ░ÉņåīļÉśĻ│Ā, ļö░ļØ╝ņä£ ņĀäņ▓┤ ņĀäĻĖ░ ņĀäļÅäļÅäĻ░Ć Ļ░ÉņåīĒĢ£ļŗż (ņłśņŗØ 4). Fig 6 (d)ļŖö Ļ│äļ®┤ ņןļ▓Į ņŚÉļäłņ¦ĆĻ░Ć ņŚåļŖö ņāüĒÖ®Ļ│╝ ņ׳ļŖö ņāüĒÖ®ņŚÉņä£ņØś ņĀäņ×É ņŚÉļäłņ¦Ć ļ│ä ņĀäļÅäļÅä (differential conductivity, Žā(E)ļź╝ ĒåĄĻ│äņĀü ļČäĒżļĪ£ ļéśĒāĆļéĖ ĻĘĖļ”╝ņ£╝ļĪ£, ņØ┤ ĻĘĖļ”╝ņØä ĒåĄĒĢ┤ Ļ│äļ®┤ ņןļ▓Į ņŚÉļäłņ¦ĆņŚÉ ņØśĒĢ£ ņé░ļ×ĆņØ┤ ņĀ£ļ▓Ī Ļ│äņłśņŚÉ ņ¢┤ļ¢ż ĒÜ©Ļ│╝ļź╝ ņØ╝ņ£╝ĒéżļŖöņ¦Ć ņ£ĀļÅäĒĢĀ ņłś ņ׳ļŗż. Žā(E)ļŖö ĒŖ╣ņĀĢ ņŚÉļäłņ¦Ć Eļź╝ Ļ░Ćņ¦ä ņĀäņ×ÉņØś ļåŹļÅäņÖĆ ņØ┤ļÅÖļÅäņØś Ļ│▒ņ£╝ļĪ£ņŹ©, ņØ┤ ĒĢ©ņłśļź╝ ņĀäņ▓┤ ņĀäņ×É ņŚÉļäłņ¦Ć ļ▓öņ£äņŚÉņä£ ņĀüļČäĒĢśļ®┤ Ļ▒░ņŗ£ņĀüņ£╝ļĪ£ ņĖĪņĀĢļÉśļŖö ņ×¼ļŻīņØś ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ ĻĄ¼ĒĢĀ ņłś ņ׳ļŗż. Fig 6 (d)ņŚÉņä£ ļéśĒāĆļéśļō»ņØ┤, ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć ļ®öņ╗żļŗłņ”śņØ┤ ņĀüņÜ®ļÉśļ®┤ ņןļ▓Į ņŚÉļäłņ¦Ćļ│┤ļŗż ļé«ņØĆ ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ä ņĀäņ×ÉļŖö ĻĄŁņåīĒÖöļÉ£ļŗż (localized). ĻĄŁņåīĒÖöļÉ£ ņĀäņ×Éļōż ņŚŁņŗ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ļåŹļÅäļź╝ Ļ░Ćņ¦Ćļéś (nŌēĀ0), ņØ┤ļÅÖļÅäļŖö 0ņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ (m=0), ņØ┤ ļæÉ ĒĢŁņØś Ļ│▒ņØĖ Žā(E) ĒĢ©ņłśļŖö 0ņØ┤ ļÉ£ļŗż (ņłśņŗØ 4). ļö░ļØ╝ņä£ ņØĖ ņĀäņ×ÉļōżņŚÉ ņØśĒĢ£ ņ░©ļÅÖ ņĀäļÅäļÅäļŖö 0ņØ┤ ļÉśņ¢┤ (E’╝£ E b), Fig 6 (d)ņØś ņśżļźĖņ¬ĮņŚÉ Ēæ£ņŗ£ļÉ£ Ļ▓āņ▓śļ¤╝ ļ╣äļīĆņ╣ŁņĀüņØĖ Žā(E)ļź╝ ļ│┤ņØĖļŗż. ņŚ¼ĻĖ░ņä£ ĒÄśļź┤ļ»Ė ļĀłļ▓©ņØ┤ ļ│ĆĒĢśņ¦Ć ņĢŖļŖöļŗżļŖö ņĀÉņØ┤ ņżæņÜöĒĢ£ļŹ░, ņØ┤ļŖö ņŚÉļäłņ¦Ć ņןļ▓ĮņØ┤ ņĀäņ×Éļź╝ ņøĆņ¦üņØ┤ņ¦Ć ļ¬╗ĒĢśĻ▓īļ¦ī ļ¦īļōĀ Ļ▓āņØ┤ņ¦Ć, ņĀäņ×É ĻĘĖ ņ×Éņ▓┤ļź╝ ņĀ£Ļ▒░ĒĢ£ Ļ▓āņØ┤ ņĢäļŗłĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
Žā(E)ļŖö ļ¬©ĒŖĖ Ļ│ĄņŗØ (Mott formula)ņØä ĒåĄĒĢ┤ ņĀ£ļ▓Ī Ļ│äņłśņÖĆ ņŚ░Ļ┤ĆļÉĀ ņłś ņ׳ļŗż17.
ņłśņŗØ 8ņŚÉ ņØśĒĢśļ®┤, ņŚ┤ņĀä ņ×¼ļŻīņØś ņĀ£ļ▓Ī Ļ│äņłśļŖö ĒÄśļź┤ļ»Ė ļĀłļ▓©ņŚÉņä£ ln(Žā(E)) ĒĢ©ņłśņØś ņŚÉļäłņ¦ĆņŚÉ ļīĆĒĢ£ ĻĖ░ņÜĖĻĖ░ņŚÉ ļ╣äļĪĆĒĢśļ®░, ņŚ¼ĻĖ░ņä£ k B, T ļ░Å eļŖö ļ│╝ņĖĀļ¦ī ņāüņłś, ņĀłļīĆ ņś©ļÅä ļ░Å ĻĖ░ļ│Ė ņĀäĒĢśļź╝ ļéśĒāĆļéĖļŗż. ln(Žā(E)) ĻĖ░ņÜĖĻĖ░ļŖö Ļ│äļ®┤ ņןļ▓Į ņŚÉļäłņ¦ĆņŚÉ ņØśĒĢ£ ņĀäņ×ÉņØś ņäĀĒāØņĀü ņé░ļ×ĆņØ┤ ņ׳ļŖö ņāüĒÖ®ņŚÉņä£ Ēø©ņö¼ Ēü¼Ļ│Ā, ņØ┤ļŖö ņĀ£ļ▓Ī Ļ│äņłś ņŚŁņŗ£ ņ╗żņ¦ÉņØä ņØśļ»ĖĒĢ£ļŗż. ņ”ē, Ļ│äļ®┤ ņŚÉļäłņ¦Ć ņןļ▓ĮņŚÉ ņØśĒĢ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć ļ®öņ╗żļŗłņ”śņ£╝ļĪ£ ņØĖĒĢ┤ ņĀäĻĖ░ ņĀäļÅäņä▒ņØĆ ņĀĆĒĢśļÉśņ¦Ćļ¦ī ĻĘĖ ļīōĻ░ĆļĪ£ ņĀ£ļ▓Ī Ļ│äņłśļŖö Ē¢źņāüņŗ£Ēé¼ ņłś ņ׳ņØīņØ┤ ņ”Øļ¬ģļÉ£ļŗż. ļśÉĒĢ£, ņĀäĻĖ░ ņĀäļÅäņä▒ņØä ņ¢╝ļ¦łļéś ļ¦ÄņØ┤ ĒؼņāØĒĢśĻ│Ā, ņĀ£ļ▓Ī Ļ│äņłśļź╝ ņ¢╝ļ¦łļéś ļåÆņØ╝ ņłś ņ׳ļŖöņ¦ĆļŖö ņ×¼ļŻīņØś ņäĀĒāØņ£╝ļĪ£ ņ¢┤ļŖÉ ņĀĢļÅä ņĪ░ņĀł Ļ░ĆļŖźĒĢśļŗżļŖö Ļ▓░ļĪĀļÅä ņ¢╗ņØä ņłś ņ׳ļŗż. ņ”ē, ņןļ▓ĮņØś ļåÆņØ┤ļŖö ļ│ĄĒĢ® ņŚ┤ņĀä ņåīņ×¼ņŚÉ ņ¢┤ļ¢ż ņ×¼ļŻīĻ░Ć ļōżņ¢┤Ļ░Ćņä£ ņØ┤ļŻ©ļŖö Ļ│äļ®┤ņŚÉņä£ņØś ļ░┤ļō£ ņŚÉļäłņ¦Ć ļČłņŚ░ņåŹņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ, ņśłņĖĪĻ│╝ ņäżĻ│äĻ░Ć Ļ░ĆļŖźĒĢśĻ│Ā, ņØ┤Ļ▓āņ£╝ļĪ£ ņČ£ļĀźņØĖņ×ÉņØä ņĄ£ņĀüĒÖöĒĢśļŖö ļśÉ ļŗżļźĖ Ļ░ĆļŖźņä▒ņØ┤ ņāØĻĖ┤ļŗż.
Fig 6 (e)ņØĆ ņ”ØĻ░ĆļÉ£ ņĀ£ļ▓Ī Ļ│äņłśĻ░Ć Ļ░ÉņåīĒĢ£ ņĀäĻĖ░ ņĀäļÅäļÅäņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā Ļ▓░ĻĄŁ ZTņØś Ē¢źņāüņ£╝ļĪ£ ņØ┤ņ¢┤ņ¦ł ņłś ņ׳ņØīņØä ņśłņĖĪĒĢ£ļŗż. ņØ┤ ļ®öņ╗żļŗłņ”śņØĆ ļ░śļō£ņŗ£ ņĀäĻĖ░ ņĀäļÅäļÅäņØś Ļ░Éņåīļź╝ ļČłļ¤¼ņśżĻĖ░ ļĢīļ¼ĖņŚÉ, ļåÆņØĆ ņĀäĻĖ░ ņĀäļÅäņä▒ļź╝ ņØ┤ļ»Ė ņ¦Ćļģöņ£╝ļÉś ļé«ņØĆ ņĀ£ļ▓Ī Ļ│äņłś ļĢīļ¼ĖņŚÉ ņČ£ļĀźņØĖņ×ÉņØ┤ ņ×æņØĆ ņ×¼ļŻīņŚÉļ¦ī ņĀüĒĢ®ĒĢśļŗż. ņØ┤ ĒŖ╣ņä▒ņØĆ ĻĖłņåŹņØś ĒŖ╣ņä▒Ļ│╝ ņל ņØ╝ņ╣śĒĢśļ®░, ņØ┤Ļ▓āņØ┤ ĒŖ╣Ē׳ ĻĖłņåŹ ĻĖ░ļ░śņØś ļ│ĄĒĢ® ņ×¼ļŻīņŚÉņä£ ņØ┤ ņČ£ļĀźņØĖņ×É Ē¢źņāü ļ®öņ╗żļŗłņ”ś ņŚÉ ļīĆĒĢ£ ļģ╝ņØśĻ░Ć ņŗ£ņ×æļÉ£ ņØ┤ņ£ĀņØ┤ļŗż13. ņØ┤ņŚÉ ļ░śĒĢ┤, ļ│ĆņĪ░ ļÅäĒĢæ ļ®öņ╗żļŗłņ”śņØĆ ņĀ£ļ▓Ī Ļ│äņłśļź╝ ļ¢©ņ¢┤ļ£©ļ”¼ņ¦Ć ņĢŖĻ│Ā ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ ņ”ØĻ░Ćņŗ£Ēé©ļŗżļŖö ņĀÉņŚÉņä£, ļÅäĒĢæļÉśņ¦Ć ņĢŖņØĆ ļ░śļÅäņ▓┤ ņåīņ×¼ņŚÉņä£ ļŹö ņĀüĒĢ®ĒĢśļŗżļŖö ļīĆņĪ░ļź╝ ĒĢĀ ņłś ņ׳ļŗż.
Fig 6 (e)ņŚÉ ņ¢ĖĻĖēļÉ£ ļ¦żņÜ░ Ēü░ ZTļŖö Ļ│äļ®┤ņŚÉņä£ņØś ņØīĒ¢źņ¢æņ×ÉņØś ņØ┤ļÅÖ, ņ”ē ņŚ┤ ņĀäļÅäĻ░Ć ļ░®ĒĢ┤ļ░øĻĖ░ ļĢīļ¼ĖņŚÉ ņØ╝ņ¢┤ļéĀ ņłś ņ׳ļŗż. ņØ┤ņĀäņŚÉ ņ¢ĖĻĖēĒ¢łļō»ņØ┤, ņØīĒ¢źņ¢æņ×ÉņØś ĒÅēĻĘĀ ņ×Éņ£Ā Ļ▓ĮļĪ£ļŖö ņØ╝ļ░śņĀüņ£╝ļĪ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ĒÅēĻĘĀ ņ×Éņ£Ā Ļ▓ĮļĪ£ļ│┤ļŗż Ēø©ņö¼ ļŹö Ēü¼ļŗż. Fig 6 (e)ņŚÉņä£ļŖö 5 nm ŌĆō 20 nmņŻ╝ĻĖ░ņØś Ļ│äļ®┤ņØä Ļ░Ćņ¦ä ņ┤łĻ▓®ņ×É (superlattice)Ļ░Ć Ļ░ĆņĀĢļÉśņŚłņ£╝ļ»ĆļĪ£, ņØīĒ¢źņ¢æņ×ÉļŖö ņĀäņ×É ņØ┤ņāüņ£╝ļĪ£ ļŹö ļ¦ÄņØ┤ ņé░ļ×ĆļÉĀ Ļ▓āņØ┤ļŗż. ņØīĒ¢źņ¢æņ×ÉņØś ļ╣łļ▓łĒĢ£ ņé░ļ×ĆņØĆ ņŚ┤ ņĀäļÅäļÅäļź╝ ~ 1 W/m┬Ę KņŚÉ ņØ┤ļź╝ ļĢīĻ╣īņ¦Ć Ēü¼Ļ▓ī ņ¢ĄņĀ£ĒĢĀ Ļ▓āņ£╝ļĪ£ ņČöņé░ļÉśņŚłĻ│Ā, ņØ┤ļŖö ļ▓īĒü¼ ĻĖłņåŹņØś ņŚ┤ ņĀäļÅäļÅäļ│┤ļŗż ņłśļ░▒ļ░░ Ļ░Ćļ¤ē ņ×æņØĆ Ļ▓āņØ┤ļŗż.
ļ│ĄĒĢ® ņ×¼ļŻī ļé┤ Ļ│äļ®┤ņŚÉņä£ņØś ņŚÉļäłņ¦Ć ņןļ▓ĮņØä ĒåĄĒĢ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×ĆņØĆ ņŗżņĀ£ļĪ£ ņČ£ļĀźņØĖņ×É ņ”ØĻ░ĢņØä ņØ┤ļüīņ¢┤ ļé╝ ņłś ņ׳ņØīņØ┤ ņŗżņĀ£ ņŗżĒŚśņ£╝ļĪ£ļÅä ņ”Øļ¬ģļÉśņŚłļŗż (Fig 7). ĒĢ┤ļŗ╣ ņ×¼ļŻīļŖö Ag ļéśļģĖ ņ×ģņ×Éļź╝ ĒżĒĢ©ĒĢśļŖö Sb2 Te3 ļ¦żĒŖĖļ”ŁņŖżļØ╝ļŖö ļ│ĄĒĢ® ņ×¼ļŻīņØ┤ļŗż. ņŚ¼ĻĖ░ņä£ pĒśĢ Sb2 Te3 ļ¦żĒŖĖļ”ŁņŖżļŖö ņØ┤ļ»Ė ņĄ£ņ▓©ļŗ© ņŚ┤ņĀä ņåīņ×¼ļĪ£, ņĀäĻĖ░ ņĀäļÅäļÅäĻ░Ć ~ 70 S/cmļĪ£ ļ│┤ĒåĄņØś ĻĖłņåŹļ│┤ļŗżļŖö ļé«Ļ│Ā, ĒåĄņāüņĀüņØĖ ļ░śļÅäņ▓┤ļ│┤ļŗżļŖö ļåÆņØĆ ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ Ļ░Ćņ¦ĆĻ│Ā ņ׳ļŗż. ņØ┤ ņŚ░ĻĄ¼ņØś ĒĢĄņŗ¼ņØĆ Ag ļéśļģĖ ņ×ģņ×ÉņÖĆ Sb2 Te3 ņé¼ņØ┤ Ļ│äļ®┤ņŚÉņä£ ņČ£ļĀźņØĖņ×É ņ”ØĻ░ĢņØä ņ£äĒĢ┤ ņĀüņĀłĒĢ£ ļåÆņØ┤ņØś ņŚÉļäłņ¦Ć ņןļ▓ĮņØ┤ ņāØĻĖ░ļÅäļĪØ ĒĢ£ ņ×¼ļŻīņØś ņäĀĒāØņŚÉ ņ׳ļŗż. ņØ┤ņĀ£Ļ╣īņ¦Ć ņäżļ¬ģļÉ£ Ļ│äļ®┤ ņןļ▓Į ņŚÉļäłņ¦ĆņŚÉ ņØśĒĢ£ ņĀäņ×É ņé░ļ×Ć ļ®öņ╗żļŗłņ”śņŚÉ ļö░ļź┤ļ®┤, ĻĖłņåŹņØĖ Ag ļéśļģĖ ņ×ģņ×ÉĻ░Ć ņĀäņ×Éļź╝ ĒåĄĻ│╝ņŗ£Ēéżņ¦Ć ņĢŖĻ│Ā ņé░ļ×Ćņŗ£ĒéżļŖö ņ×¼ļŻīļĪ£ ņō░ņØĖļŗżļŖö ņĀÉņØ┤ ļåĆļØ╝ņÜĖ ņłś ņ׳ļŗż. ņŚ¼ĻĖ░ņä£ņØś Ag ļéśļģĖ ņ×ģņ×ÉļŖö pĒśĢ Sb2 Te3ņŚÉņä£ ņć╝ĒŖĖĒéż ņןļ▓Į (Schottky barrier)ņØä ĒśĢņä▒ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ, pĒśĢ Sb2 Te3ļź╝ ĒåĄĒĢ┤ ņØ┤ļÅÖĒĢśļŖö ņĀĢĻ│ĄņØä ļ░®ĒĢ┤ĒĢĀ ņłś ņ׳ļŗż. ļśÉĒĢ£, ņØ┤ Ļ▓ĮņÜ░ņŚÉņä£ Ag ļéśļģĖ ņ×ģņ×ÉļŖö ņä£ļĪ£ ņČ®ļČäĒĢ£ Ļ│ĄĻ░äņØä ļæÉĻ│Ā ļČäļ”¼ļÉśņ¢┤ ņ׳ņ¢┤ņä£, Ag ļéśļģĖ ņ×ģņ×ÉŌĆÖļ¦īŌĆÖņØä ĒåĄĒĢ£ ņĀĢĻ│ĄņØś ņĀäļÅäļŖö ļČłĻ░ĆļŖźĒĢśļŗż.
Fig.┬Ā7.
Ag ļéśļģĖ ņ×ģņ×Éļź╝ ĒżĒĢ©ĒĢśļŖö pĒśĢ Sb2 Te3 ļ¦żĒŖĖļ”ŁņŖżņØś Ļ│äļ®┤ņŚÉņä£ ņć╝ĒŖĖĒéż ņןļ▓ĮņØ┤ ņāØĻ▓©ļéśĻ│Ā, ņØ┤ļŖö ņŚÉļäłņ¦Ć ņØśņĪ┤ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×ĆņØä ņØ╝ņ£╝Ēé©ļŗż. ļé«ņØĆ ņÜ┤ļÅÖ ņŚÉļäłņ¦Ćļź╝ Ļ░Ćņ¦ä ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļ¦īņØ┤ ņäĀĒāØņĀüņ£╝ļĪ£ ņé░ļ×ĆļÉśĻ│Ā, ņØ┤ļŖö ņĀ£ļ▓Ī Ļ│äņłśņØś ļ│ĆĒÖöļź╝ ņ£ĀļÅäĒĢśņŚ¼ ņČ£ļĀźņØĖņ×ÉņØä ņ”ØĻ░Ćņŗ£Ēé©ļŗż. Figure from Silver-based intermetallic heterostructures in Sb2 Te3 thick films with enhanced thermoelectric power factors and used with permission from the American Chemical Society11.
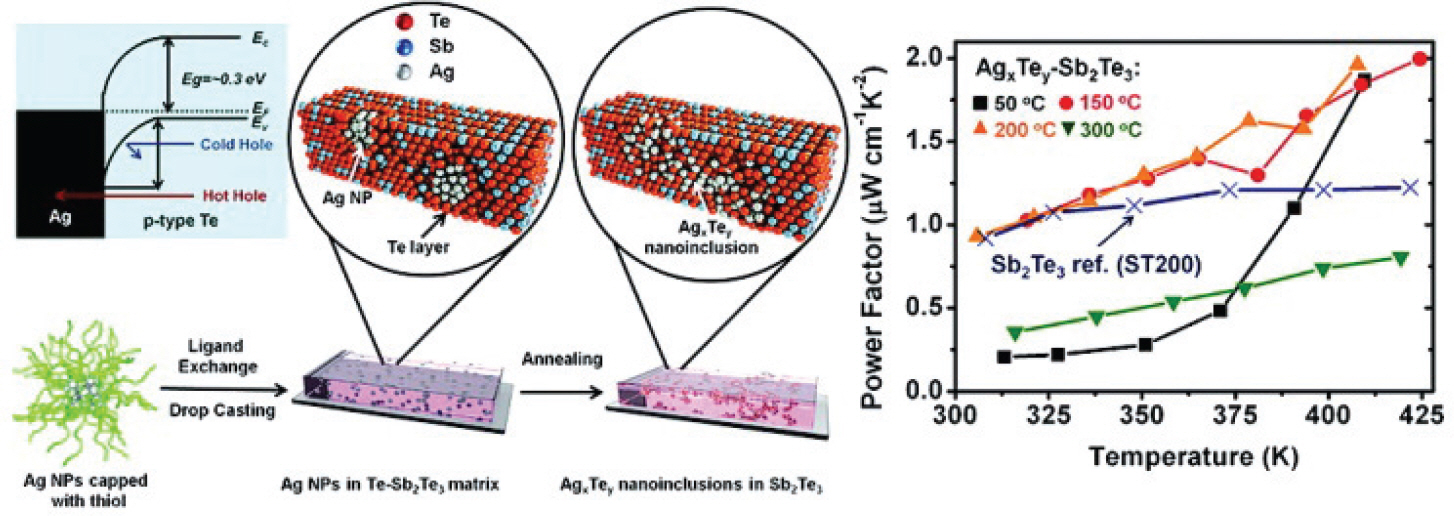
ņć╝ĒŖĖĒéż ņןļ▓ĮņØä ļ¦īļōĀ Ag ļéśļģĖ ņ×ģņ×É ļĢīļ¼ĖņŚÉ Žā(E)ļŖö ĒÄśļź┤ļ»Ė ļĀłļ▓© ņØĖĻĘ╝ņŚÉņä£ ņĢäņŻ╝ Ēü░ ĻĖ░ņÜĖĻĖ░ļź╝ Ļ░Ćņ¦ĆĻ▓ī ļÉ£ļŗż (Fig 6 (d)). ņØ┤ļĪ£ ņØĖĒĢ┤ ņĀ£ļ▓Ī Ļ│äņłśļŖö ĒÖĢļīĆļÉśĻ│Ā (ņłśņŗØ 8), ņČ£ļĀźņØĖņ×ÉļÅä Ē¢źņāüļÉ£ļŗż (Fig 7). ļśÉĒĢ£ Sb2 Te3ļź╝ ĒåĄĒĢ┤ ņĀäļÅäļÉśļŹś ņØīĒ¢źņ¢æņ×ÉĻ░Ć Ag ļéśļģĖ ņ×ģņ×ÉņÖĆņØś Ļ│äļ®┤ņŚÉņä£ ņ×ÉņŻ╝ ņé░ļ×ĆļÉśņŚł ĻĖ░ ļĢīļ¼ĖņŚÉ ņŚ┤ ņĀäļÅäļÅäņØś Ļ░Éņåī ĒÜ©Ļ│╝ļÅä ļ░£ņāØĒĢśņśĆļŗż10,11. ņØ┤ļŖö ņČ£ļĀźņØĖņ×ÉņØś ņ”ØĻ░Ģ ņØ┤ņÖĖņŚÉļÅä ZTĻ░Ć ņČöĻ░ĆņĀüņ£╝ļĪ£ ņāüņŖ╣ĒĢĀ ņłś ņ׳ļŖö ņÜöņØĖņØä ņĀ£Ļ│ĄĒĢ£ļŗż.
Ļ▓░ļĪĀ
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ļ│ĄĒĢ® ņŚ┤ņĀä ņ×¼ļŻīņŚÉņä£ņØś ņČ£ļĀźņØĖņ×É ņ”ØĻ░Ģ ļ®öņ╗żļŗłņ”śņØĖ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć (energy-dependent charge carrier scattering)Ļ│╝ ļ│ĆņĪ░ ļÅäĒĢæ (modulation doping)ņŚÉ ļīĆĒĢ┤ ņé┤ĒÄ┤ļ│┤ņĢśļŗż. ĻĘ╝ļ│ĖņĀüņ£╝ļĪ£ļŖö 2Ļ░Ćņ¦Ć ļ®öņ╗żļŗłņ”ś ļ¬©ļæÉ ņČ£ļĀźņØĖņ×ÉņØś Ē¢źņāüņØä ĒåĄĒĢ┤ ZTņØś ņ”ØļīĆļź╝ ļÅäļ¬©ĒĢśļŖö ņĀäļץņØ┤ļŗż. ļśÉĒĢ£ ļ│ĄĒĢ® ņ×¼ļŻīļź╝ ņĘ©ĒĢśļ®┤ ņØīĒ¢źņ¢æņ×É (phonon)ņØś ņé░ļ×ĆņØ┤ ļ│┤ņןļÉśļ®┤ņä£ ņŚ┤ ņĀäļÅäļÅäĻ░Ć ņ¢ĄņĀ£ļÉśĻ│Ā, ņØ┤ ĒÜ©Ļ│╝ņŚÉ ņØśĒĢ┤ņä£ļÅä ZTņØś ņāüņŖ╣ņØ┤ ņØ╝ņ¢┤ļéśĻĖ░ļÅä ĒĢ£ļŗż. ļ│ĆņĪ░ ļÅäĒĢæņØĆ ņĀ£ļ▓Ī Ļ│äņłśņØś ĒĢśĒ¢ź ņŚåņØ┤ ņĀäĻĖ░ ņĀäļÅäļÅäņØś ņāüņŖ╣ņØä ļÅäļ¬©ĒĢśņŚ¼ ņČ£ļĀźņØĖņ×ÉņØä ļŖśņØ┤ļĀżļŖö ņĀäļץņØ┤ļŗż. ņĀäĻĖ░ ņĀäļÅäļÅäļŖö ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ļåŹļÅäņÖĆ ņĀäĒĢś ņØ┤ļÅÖļÅäņØś Ļ│▒ņŚÉ ļ╣äļĪĆĒĢśļŖöļŹ░, ņ┤Ø ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś Ļ░»ņłśļź╝ ĻĘĖļīĆļĪ£ ļ│┤ņĪ┤ĒĢ£ņ▒äļĪ£ ņĀäĒĢś ņØ┤ļÅÖļÅäĻ░Ć ļåÆņØĆ ņ×¼ļŻīņŚÉņä£ ļīĆļČĆļČäņØś ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć ņĀäļÅäļÉśļÅäļĪØ ņ£ĀļÅäĒĢśļŖö Ļ▓āņØ┤ ĒĢĄņŗ¼ņØ┤ļŗż. ņØ┤ņŚÉ ļ░śĒĢ┤, ņĀäĒĢś ņ║Éļ”¼ņ¢┤ ņé░ļ×Ć ļ®öņ╗żļŗłņ”śņØĆ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ņØś ņØ┤ļÅÖļÅäņÖĆ ņĀäĻĖ░ ņĀäļÅäļÅäļź╝ ņØ╝ļČĆ ĒؼņāØĒĢśņŚ¼, ņĀ£ļ▓Ī Ļ│äņłśļź╝ ĒéżņÜ░ļŖö ņĀäļץņØ┤ļŗż. ņ▓½ ļ▓łņ¦Ė ļŗ©Ļ│äļŖö ļ│ĄĒĢ® ņ×¼ļŻī ņżæ ĒĢ£ Ļ░Ćņ¦Ć ņ×¼ļŻīļĪ£ ņĀäĒĢś ņ║Éļ”¼ņ¢┤ļōż ņżæ ņŚÉļäłņ¦ĆĻ░Ć ņ×æņØĆ Ļ▓āļōżņØ┤ ĒåĄĒ¢ēĒĢĀ ņłś ņŚåļŖö ņŚÉļäłņ¦Ć ņןļ▓ĮņØä ņäżņ╣śĒĢśņŚ¼, ĻĘĖļōżņØś ņØ┤ļÅÖļÅäļź╝ ļ¢©ņ¢┤ļ£©ļ”¼ļŖö Ļ▓āņØ┤ļŗż. ņØ┤ļĪ£ ņØĖĒĢ┤, ņĀäĒĢś ņ║Éļ”¼ņ¢┤Ļ░Ć Ļ░Ćņ¦ä ņŚÉļäłņ¦Ćļ│ä ņĀäļÅäļÅä (differential conductivity)Ļ░Ć ļ░öļĆīņ¢┤ ņĀ£ļ▓Ī Ļ│äņłśĻ░Ć ņāüņŖ╣ĒĢ£ļŗż. ņŚ┤ņŚŁĒĢÖņĀüņØĖ Ļ┤ĆņĀÉņŚÉņä£ļŖö, ņ║Éļ”¼ņ¢┤ 1Ļ░£Ļ░Ć ņłśņåĪĒĢśļŖö ĒÅēĻĘĀ ņŚÉļäłņ¦ĆņØś Ēü¼ĻĖ░ļź╝ ĒéżņøĆņ£╝ļĪ£ņŹ©, ņĀ£ļ▓Ī Ļ│äņłśļź╝ ņś¼ļ”¼ļŖö ļ░®ņŗØņØ┤ļØ╝Ļ│Ā ĻĖ░ņłĀĒĢĀ ņłś ņ׳ļŗż.









