1. ņä£ļĪĀ
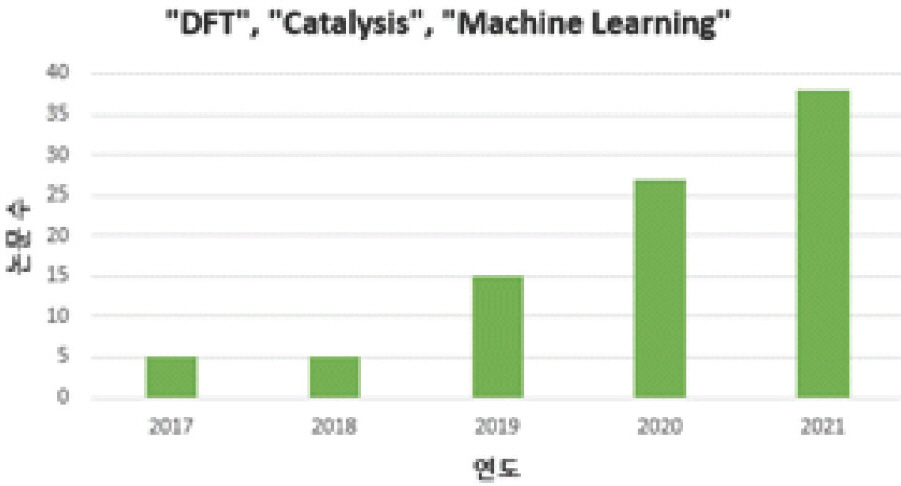
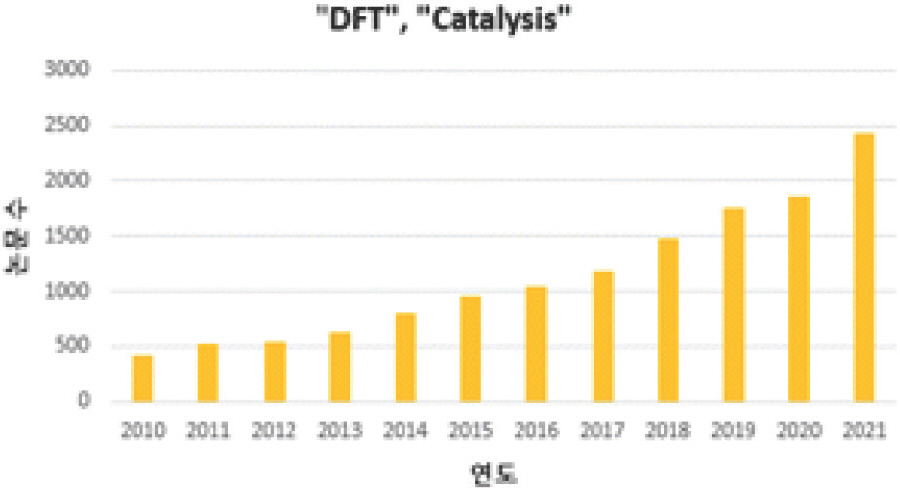
ņŗĀņ×¼ņāØ ņŚÉļäłņ¦Ć ĻĖ░ļ░ś ņé¼ĒÜīļź╝ ņ£äĒĢ┤ņä£ļŖö ņä▒ļŖźņØ┤ ņÜ░ņłśĒĢśĻ│Ā Ļ░ĆĻ▓® Ļ▓Įņ¤üļĀźņØ┤ ļåÆņØĆ ņ┤ēļ¦żļź╝ ĒĢäņłśņĀüņ£╝ļĪ£ Ļ░£ļ░£ĒĢ┤ņĢ╝ ĒĢ£ļŗż. ņ┤ēļ¦ż Ļ░£ļ░£ņØä ņ£äĒĢ┤ ņĀäĒåĄņĀüņ£╝ļĪ£ ņŗ£Ē¢ēņ░®ņśż ĻĖ░ļ▓Ģ (trial-and-error)ņØä ĒåĄĒĢśņŚ¼ ņ┤ēļ¦żļź╝ Ļ░£ļ░£ĒĢ┤ņÖöĻ│Ā ļŗżņ¢æĒĢ£ ņÜ░ņłś ņ┤ēļ¦żļź╝ Ļ░£ļ░£ĒĢ£ ļ░ö ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī ĒÖ£ņä▒, ņäĀĒāØņä▒, ņĢłņĀĢņä▒, Ļ░ĆĻ▓® ļō▒ ļ¬©ļōĀ ņÜöņåīļź╝ ļ¦īņĪ▒ĒĢśļŖö ņØ┤ņāüņĀüņØĖ ņ┤ēļ¦żļŖö ņŚ¼ņĀäĒ׳ ļ│┤Ļ│ĀļÉśņ¦Ć ņĢŖņĢśĻĖ░ ļĢīļ¼ĖņŚÉ, ņØ┤ ļ¼ĖņĀ£ļź╝ ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ┤ ņ╗┤Ēō©Ēä░ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ĒÖ£ņÜ®ĒĢśļŖö ņĀæĻĘ╝ļ▓ĢņØ┤ ņĀ£ņŗ£ļÉśņŚłļŗż[1]. 1950 ļģäļīĆ ņØ┤Ēøä ņ╗┤Ēō©Ēä░ ĒĢśļō£ņø©ņ¢┤ņÖĆ ņåīĒöäĒŖĖņø©ņ¢┤ņØś ļłłļČĆņŗĀ ļ░£ņĀä ļŹĢļČäņŚÉ Ļ│äņé░Ļ│╝ĒĢÖņØä ĒåĄĒĢ£ ņŗĀņåŹĒĢ£ ņ┤ēļ¦ż ļ¼╝ņ¦ł ĒāÉņāēņØ┤ ņŻ╝ļ¬®ļ░øĻ│Ā ņ׳ļŗż. ĒŖ╣Ē׳ ņ¦Ćļé£ 20ļģäĻ░ä ļ░ĆļÅäļ▓öĒĢ©ņłśņØ┤ļĪĀ (Density Functional Theory, DFT) ĻĖ░ļ░śņØś ņØ┤ļĪĀĻ│╝ĒĢÖņĀü ļ░®ļ▓ĢņØ┤ ņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ ņ£ĀņÜ®ĒĢ£ ļ░®ļ▓ĢļĪĀņ£╝ļĪ£ ņé¼ņÜ®ļÉśņ¢┤ ņÖöļŗż. Web of ScienceņŚÉņä£ ŌĆ£DFTŌĆØņÖĆ ŌĆ£CatalysisŌĆØļØ╝ļŖö Ēéżņøīļō£ļź╝ ļÅÖņŗ£ņŚÉ Ļ▓Ćņāēņŗ£ ņČ£ĒīÉļÉ£ ļģ╝ļ¼Ė ņłśļŖö 2010ļģä 500ĒÄĖ ļ»Ėļ¦īņŚÉņä£, 2021ļģä 2,500ĒÄĖņ£╝ļĪ£ 5ļ░░ ņ”ØĻ░ĆĒĢ£ Ļ▓āņØä ņĢī ņłś ņ׳ļŗż [Fig 1].
Fig.┬Ā1.
Web of Science ņāü ŌĆ£DFTŌĆØņÖĆ ŌĆ£CatalysisŌĆØņŚÉ Ļ┤ĆĒĢ£ ņŚ░ļÅäļ│ä ļģ╝ļ¼Ė ņłś (2022.05 ĻĖ░ņżĆ)
ņØ┤ ņżæ ļŗżņłśņØś ņŚ░ĻĄ¼Ļ░Ć ļ│Ė ņ┤ØņäżņŚÉņä£ ņåīĻ░£ĒĢĀ ņ┤ēļ¦ż ļ░śņØæņØĖ ņé░ņåī Ļ┤ĆļĀ© ņĀäĻĖ░ĒÖöĒĢÖ ļ░śņØæņ£╝ļĪ£, ņŚ░ļŻīņĀäņ¦Ć ņ¢æĻĘ╣ ļ░śņØæņØĖ ņé░ņåīĒÖśņøÉ ļ░śņØæ (Oxygen Reduction Reaction, ORR)Ļ│╝ ņłśņĀäĒĢ┤ ņØīĻĘ╣ ļ░śņØæņØĖ ņé░ņåīļ░£ņāØ ļ░śņØæ (Oxygen Evolution Reaction, OER)ņØ┤ļŗż. ļæÉ ļ░śņØæņØĆ ņŚ░ļŻīņĀäņ¦ĆņÖĆ ņłśņĀäĒĢ┤ņØś ĒĢĄņŗ¼ ļ░śņØæņ£╝ļĪ£ Ēśäņ×¼ Ļ░Æļ╣äņŗ╝ ĻĘĆĻĖłņåŹ ņ┤ēļ¦żļź╝ ļīĆņ▓┤ĒĢĀ Ļ│ĀĒÖ£ņä▒ņØś ļ╣äĻĘĆĻĖłņåŹ ĻĖ░ļ░ś ņ┤ēļ¦żļź╝ ĒĢäņÜöļĪ£ ĒĢ£ļŗż. ņØ┤ņŚÉ DFT ļź╝ ņØ┤ņÜ®ĒĢ£ Ļ│äņé░Ļ│╝ĒĢÖņĀü ņŚ░ĻĄ¼ļ░®ļ▓ĢļĪĀņØĆ ļ░śņØæņżæĻ░äņ▓┤ ĒØĪņ░® ņŚÉļäłņ¦Ć Ļ░äņØś ņäĀĒśĢ Ļ┤ĆĻ│ä, ņ┤ēļ¦ż Ēæ£ļ®┤ņØś d-band center ņÖĆ ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś ņäĀĒśĢ Ļ┤ĆĻ│äļź╝ ĒåĄĒĢ┤ ņÜ░ņłśĒĢ£ ņĀäĻĖ░ĒÖöĒĢÖ ņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ Ēü¼Ļ▓ī ĻĖ░ņŚ¼ĒĢśņśĆļŗż[2]. DFTĻ░Ć ĒĢĄņŗ¼ņĀüņØĖ ņØ┤ļĪĀ ļ░Å Ļ│ĄĒĢÖ ņŚ░ĻĄ¼ņŚÉ ļø░ņ¢┤ļé£ ņä▒Ļ│╝ņÖĆ Ļ░ĆļŖźņä▒ņØä ļ│┤ņśĆņØīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā, Ļ│äņé░ĒĢĀ ņøÉņ×ÉĻĄ¼ņĪ░Ļ░Ć ļ│Ąņ×Ī, ļŗżņ¢æĒĢ┤ņ¦Ćļ®░ ņØ┤ņŚÉ ņåīļ¬©ļÉśļŖö Ļ│äņé░ ņŗ£Ļ░ä ļśÉĒĢ£ Ēü¼Ļ▓ī ņ”ØĻ░ĆĒĢśļŖö ļ¼ĖņĀ£Ļ░Ć ļ░£ņāØĒĢ£ļŗż. ļö░ļØ╝ņä£ ņØ┤ļ¤¼ĒĢ£ ĒĢ£Ļ│äļź╝ ļ│┤ņÖäĒĢĀ ĒÜ©ņ£©ņĀüņØĖ ņłśļŗ©ņØ┤ ņÜöĻĄ¼ļÉśĻ│Ā ņ׳ņ£╝ļ®░, ņśżļŖśļéĀ ņČĢņĀüļÉ£ ņ¢æņ¦łņØś DFT ļŹ░ņØ┤Ēä░ņÖĆ ĻĖ░ĒĢśĻĖēņłśņĀüņ£╝ļĪ£ ļ░£ņĀä ņżæņØĖ ĻĖ░Ļ│äĒĢÖņŖĄņØ┤ ĻĘĖ ņÜöĻĄ¼ļź╝ ļ¦īņĪ▒ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆļÉ£ļŗż[3]. [Fig 2]ļŖö [Fig 1]ņØś Ļ▓░Ļ│╝ņŚÉ ŌĆ£Machine LearningŌĆØ Ēéżņøīļō£ļź╝ ņČöĻ░ĆĒ¢łņØä ļĢīņØś Ļ▓Ćņāē Ļ▓░Ļ│╝ļĪ£, ļ╣äĻĄÉņĀü ņĄ£ĻĘ╝ņØĖ 2018ļģä ņØ┤Ēøä ĻĖ░Ļ│äĒĢÖņŖĄ Ļ┤ĆļĀ© ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£ĒĢ┤ņ¦ÉņØä ņĢī ņłś ņ׳ļŗż. ļ│Ė ņ┤ØņäżņŚÉņä£ļŖö Ļ│äņé░ĒÖöĒĢÖĻ│╝ ĻĖ░Ļ│äĒĢÖņŖĄņØä ņØ┤ņÜ®ĒĢ£ ĒÜ©Ļ│╝ņĀüņØĖ ņĀäĻĖ░ĒÖöĒĢÖ ņ┤ēļ¦ż Ļ░£ļ░£ ņé¼ļĪĆļōżņØä ņé┤ĒÄ┤ļ│┤ļ®░ Ēśäņ×¼ ļÅÖĒ¢źņØä ļģ╝ĒÅēĒĢśĻ│Āņ×É ĒĢ£ļŗż.
2. Ļ│äņé░ĒÖöĒĢÖņØä ņØ┤ņÜ®ĒĢ£ ņ┤ēļ¦ż Ļ░£ļ░£ ņŚ░ĻĄ¼
DFTļŖö ļŗżņ▓┤ (many-body) ņŗ£ņŖżĒģ£ņØś ņĀäņ×ÉĻĄ¼ņĪ░ ļČäņäØņØä ņ£äĒĢ┤ ņé¼ņÜ®ļÉ£ļŗż. ņĀäņ×É 1Ļ░£ņØś Ļ▒░ļÅÖņØä ļČäņäØĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņŖłļó░ļö®Ļ▒░ ļ░®ņĀĢņŗØņØś ĒÆĆņØ┤ļź╝ ĒåĄĒĢ┤ ĒīīļÅÖĒĢ©ņłśļź╝ ĻĄ¼ĒĢ┤ņĢ╝ ĒĢ£ļŗż. ļö░ļØ╝ņä£ NĻ░£ņØś ņĀäņ×Éļź╝ Ļ░¢ļŖö ņ×äņØś ņøÉņ×ÉņØś ņĀäņ×É ĻĄ¼ņĪ░ļź╝ ĒīīņĢģĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņ┤Ø NĻ░£ņØś ĒīīļÅÖĒĢ©ņłśļź╝ ļ¬©ļæÉ ĻĄ¼ĒĢ┤ņĢ╝ ĒĢśņ¦Ćļ¦ī, ļŗżņ▓┤ ņŗ£ņŖżĒģ£ņØś ĒīīļÅÖĒĢ©ņłśļź╝ ĻĄ¼ĒĢśĻĖ░ ņ£äĒĢ£ ĒĢ┤ņäØņĀüņØĖ ĒĢ┤ļ▓ĢņØĆ ņĪ┤ņ×¼ĒĢśņ¦Ć ņĢŖļŗż. ĒĢśņ¦Ćļ¦ī Walter KohnĻ│╝ Lu Jeu ShamņØ┤ Ļ░£ļ░£ĒĢ£ DFTļŖö ļŗżņ▓┤ ņŗ£ņŖżĒģ£ņØś ņĀäņ×ÉĻĄ¼ņĪ░ ļČäņäØņŚÉ ņ£ĀņÜ®ĒĢ£ Ēł┤ļĪ£ ņŻ╝ļ¬® ļ░øĻ│Ā ņ׳ļŗż (Walter KohnņØĆ John A. PopleĻ│╝ ĒĢ©Ļ╗ś 1998ļģäļÅä ļģĖļ▓©ĒÖöĒĢÖņāü ņłśņāü)
DFTļŖö ņŗ£ņŖżĒģ£ ļé┤ņŚÉ ņĪ┤ņ×¼ĒĢśļŖö ņĀäņ×ÉņØś ļ¬©ļōĀ ĒīīļÅÖĒĢ©ņłśļź╝ ĻĄ¼ĒĢśļŖö Ļ▓āņØ┤ ņĢäļŗī, ņĀäņ×ÉņØś ļ░ĆļÅäļź╝ ĒåĄĒĢ┤ ņŗ£ņŖżĒģ£ ļé┤ņØś ņāüĒśĖņ×æņÜ®ņØä ļČäņäØĒĢśļŖö ļ░®ļ▓ĢņØ┤ļŗż. ņØ┤ ļ░®ļ▓ĢņØĆ ņŗ£ņŖżĒģ£ ļé┤ņØś ļ░öļŗźņāüĒā£ ņĀäņ×Éļ░ĆļÅäĻ░Ć ĒĢśļéśņØś ļ▓öĒĢ©ņłś (functional)ņŚÉ ļīĆņØæļÉ£ļŗżļŖö ļ░£Ļ▓¼Ļ│╝ ĒĢ©Ļ╗ś, ņØ┤ ļ▓öĒĢ©ņłśņØś ņŚÉļäłņ¦Ćļź╝ ņĄ£ņåīĒÖöĒĢśļŖö ņĀäņ×Éļ░ĆļÅäĻ░Ć ļŗżņ▓┤ņŚÉņä£ņØś ņŖłļó░ļö®Ļ▒░ ļ░®ņĀĢņŗØņØś ĒĢ┤ (ĒīīļÅÖĒĢ©ņłś)ļØ╝ļŖö ņøÉļ”¼ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņĀäņ×ÉĻĄ¼ņĪ░ļź╝ Ļ│äņé░ĒĢ£ļŗż. ĻĘĖļ¤¼ļéś ņĀäņ×ÉņØś Ļ░£ņłśĻ░Ć ļ¦ÄņĢäņ¦łņłśļĪØ ĒīīļÅÖĒĢ©ņłśņØś ņłś ņŚŁņŗ£ ļ¦ÄņĢäņ¦ĆĻĖ░ņŚÉ ņĀäņ×Éļ░ĆļÅäļź╝ ĻĄ¼ĒĢśĻĖ░ ņ£äĒĢ£ Ļ│äņé░ņØ┤ ļ│Ąņ×ĪĒĢ┤ņ¦äļŗż. ņØ┤ļź╝ ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ┤ ņĄ£ņÖĖĻ░ü ņĀäņ×Éļź╝ ņĀ£ņÖĖĒĢ£ ņøÉņ×ÉĒĢĄĻ│╝ ņĀäņ×ÉļŖö ĒĢśļéśņØś ļ¬Ėņ▓śļ¤╝ Ļ▒░ļÅÖĒĢ£ļŗżļŖö ņ£Āņé¼ĒżĒģÉņģ£ (pseudopotential)Ļ│╝ ņĀäņ×ÉņØś ņ£äņ╣śĻ░Ć ļ░öļĆīņŚłņØä ļĢī ļ░£ņāØĒĢśļŖö ņŚÉļäłņ¦Ć ņ░©ņØ┤ļź╝ ļ│┤ņĀĢĒĢ┤ņŻ╝ļŖö ĻĄÉĒÖś-ņāüĻ┤Ć ĒżĒģÉņģ£ ļ▓öĒĢ©ņłś (Exchange-Correlation Potential Functional)ļØ╝ļŖö Ļ░£ļģÉ ļÅäņ×ģĒĢśņśĆĻ│Ā, ņĀüņĀłĒĢ£ ņ┤łĻĖ░ ĒīīļÅÖĒĢ©ņłśļĪ£ļČĆĒä░ ņ┤łĻĖ░ ņŚÉļäłņ¦Ćļź╝ ĻĄ¼ĒĢśĻ│Ā ĻĄ¼ĒĢ£ ņŚÉļäłņ¦Ćļź╝ ņØ┤ņÜ®ĒĢ┤ ļŗżņŗ£ ĒīīļÅÖĒĢ©ņłśļź╝ ĻĄ¼ĒĢśĻ│Ā ņśżņ░©ļź╝ ņżäņŚ¼Ļ░Ćļ®░ ļ░śļ│Ą Ļ│äņé░ņØä ĒĢśļŖö ļ░®ņŗØņØĖ self-consistent ļ░®ņŗØņØä ĒåĄĒĢ┤ ļ░öļŗźņāüĒā£ņØś ņĀäņ×ÉĻĄ¼ņĪ░ļź╝ Ļ│äņé░ĒĢ£ļŗż.
ņØ┤ļ¤¼ĒĢ£ DFTļŖö ļŗżņ▓┤ ņŗ£ņŖżĒģ£ņØś ĒīīļÅÖĒĢ©ņłśļź╝ ĻĄ¼ĒĢśļŖö Ļ▓āļ│┤ļŗż Ēø©ņö¼ ĒÜ©ņ£©ņĀüņØ┤ļ®░ ļ│Ąņ×ĪĒĢ£ ņ¢æņ×ÉņŚŁĒĢÖ ņäĖĻ│äļź╝ Ēø©ņö¼ ņēĮĻ▓ī ņØ┤ĒĢ┤ĒĢĀ ņłś ņ׳ļŗżļŖö ņןņĀÉņØ┤ ņ׳ļŗż. ļ│┤ĒÄĖņĀüņ£╝ļĪ£ DFTļŖö Ļ│Āņ▓┤ņØś ņĀäņ×ÉĻĄ¼ņĪ░ ļČäņäØņŚÉ ļ¦ÄņØ┤ ņé¼ņÜ®ļÉśļ®░, ņĄ£ĻĘ╝ņŚÉļŖö ņ╗┤Ēō©Ēīģ ĒĢśļō£ņø©ņ¢┤ņØś ĒÅŁļ░£ņĀüņØĖ ļ░£ņĀäņ£╝ļĪ£ ļ░░Ēä░ļ”¼, ņ┤ēļ¦ż ļō▒ ņŚ¼ļ¤¼ ļ¼╝ļ”¼, ĒÖöĒĢÖ ļČäņĢ╝ņØś ņŚ░ĻĄ¼ņŚÉņä£ ļäÉļ”¼ ņé¼ņÜ®ļÉśĻ│Ā ņ׳ļŗż[4, 5].
ļ│Ė ņĀłņŚÉņä£ļŖö ņĀäĻĖ░ĒÖöĒĢÖņĀü ņé░ņåīĒÖśņøÉ ļ░śņØæĻ│╝ ņé░ņåīļ░£ņāØ ļ░śņØæņŚÉ ļīĆĒĢ£ Ļ│äņé░ĒÖöĒĢÖņĀü ņĀæĻĘ╝ļ▓ĢņŚÉ ļīĆĒĢ┤ ņé┤ĒÄ┤ļ│┤Ļ│Āņ×É ĒĢ£ļŗż. ņé░ņåīļ░£ņāØ ļ░śņØæņØĆ ĻĘĖļ”░ ņłśņåīļź╝ ņāØņé░ĒĢśļŖö ņłśņĀäĒĢ┤ ņŗ£ņŖżĒģ£ņØś ņØīĻĘ╣ņŚÉņä£ ņØ╝ņ¢┤ļéśĻ│Ā ņé░ņåīĒÖśņøÉ ļ░śņØæņØĆ ņŚ░ļŻīņĀäņ¦Ć ņ¢æĻĘ╣ņŚÉņä£ ņØ╝ņ¢┤ļéśļŖö ļ░śņØæņØ┤ļŗż. ļæÉ ļ░śņØæņØĆ ĒÖöņäØ ņŚ░ļŻīļź╝ ļīĆņ▓┤ĒĢśņŚ¼ ņ╣£ĒÖśĻ▓ĮņĀüņØ┤Ļ│Ā ņ¦ĆņåŹ Ļ░ĆļŖźĒĢ£ ņŚÉļäłņ¦Ć ņé¼ĒÜīļź╝ ņŗżĒśäĒĢśļŖö ļŹ░ ĒĢäņłśņĀüņØĖ ļ░śņØæņØ┤Ļ│Ā, ņĄ£ĻĘ╝ ĒÖöļæÉĻ░Ć ļÉśĻ│Ā ņ׳ļŖö ņłśņåīĻ▓ĮņĀ£ņØś ĒĢĄņŗ¼ ņÜöņåīņØ┤ļ»ĆļĪ£, ļåÆņØĆ ĒÜ©ņ£©Ļ│╝ Ļ▓ĮņĀ£ņä▒ņØś ņ┤ēļ¦żļź╝ Ļ░£ļ░£ĒĢśļŖö Ļ▓āņØ┤ ĒĢäņłśņĀüņØ┤ļŗż.
2.1 ņé░ņåīĒÖśņøÉ ļ░śņØæ (Oxygen Reduction Reaction, ORR)
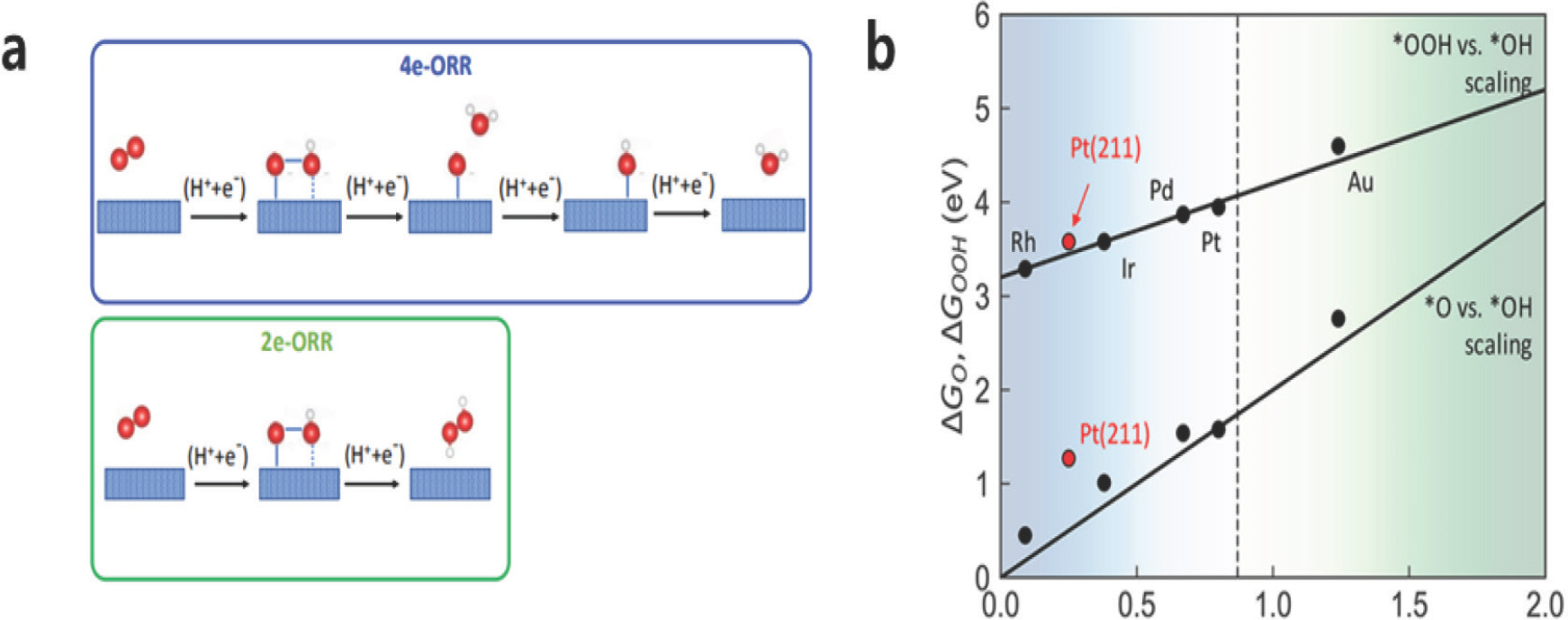
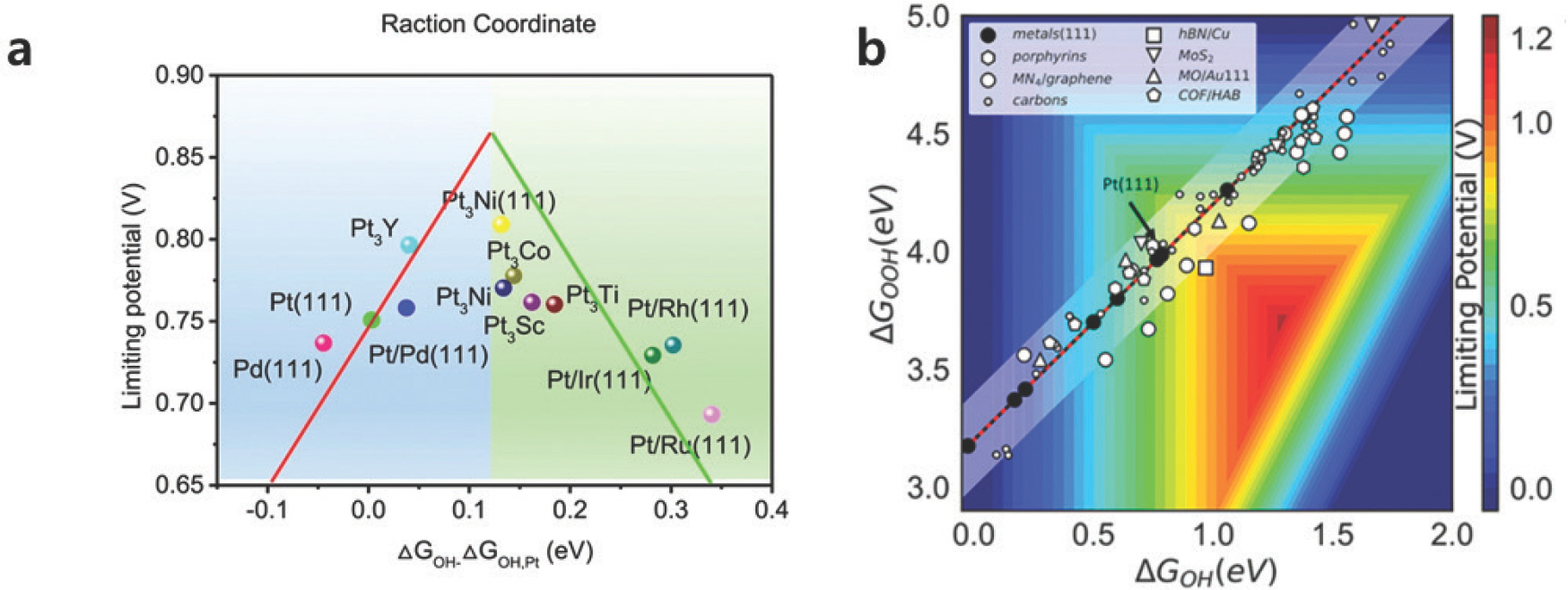
ņé░ņåīĒÖśņøÉ ļ░śņØæņØĆ ņŚ░ļŻīņĀäņ¦Ć ņ¢æĻĘ╣ņØś ĒĢĄņŗ¼ ļ░śņØæņ£╝ļĪ£ ņé░ņåī ĻĖ░ņ▓┤Ļ░Ć 4Ļ░£ņØś ņ¢æņä▒ņ×É-ņĀäņ×É ņīŹĻ│╝ ļ░śņØæĒĢśņŚ¼ ļ¼╝ļĪ£ ĒÖśņøÉļÉśļ®┤ņä£ ņŚÉļäłņ¦Ćļź╝ ļ░£ņāØĒĢśļŖö ļ░śņØæņØ┤ļŗż (ņŗØ1). ĒĢ┤ļŗ╣ ļ░śņØæņØĆ ņé░ņåī ļČäņ×É 1Ļ░£ ļŗ╣ 4Ļ░£ņØś ņ¢æņä▒ņ×É-ņĀäņ×ÉņīŹĻ│╝ ļ░śņØæĒĢśĻ│Ā 3Ļ░£ņØś ļ░śņØæņżæĻ░äņ▓┤ (OŌłŚ, OHŌłŚ, OOHŌłŚ)ļĪ£ ņØ┤ļŻ©ņ¢┤ņĀĖ ņ׳ļŗż [Fig 3a], (ņŗØ2). ņé░ņåīĻ░Ć 2Ļ░£ņØś ņ¢æņä▒ņ×É-ņĀäņ×ÉņīŹĻ│╝ ļ░śņØæĒĢśĻ│Ā 1Ļ░£ņØś ļ░śņØæņżæĻ░äņ▓┤ (OOHŌłŚ)ļ¦īņØä Ļ▒░ņ│É Ļ│╝ņé░ĒÖöņłśņåīļź╝ ņāØņä▒ĒĢśļŖö ļ░śņØæ (2e-ORR)Ļ│╝ ĻĄ¼ļČäĒĢśĻĖ░ ņ£äĒĢ┤ņä£ 4e-ORRņØ┤ļØ╝ ļČĆļźĖļŗż. Ēśäņ×¼Ļ╣īņ¦Ć ļŗżņ¢æĒĢ£ ņŚ░ĻĄ¼ļź╝ ĒåĄĒĢ┤ ļ░▒ĻĖł ņ┤ēļ¦żĻ░Ć ORRņŚÉņä£ ņÜ░ņłśĒĢ£ ņä▒ļŖźņØä ļ│┤ņŚ¼ņŻ╝ņŚłņ¦Ćļ¦ī, ļ╣äņŗ╝ Ļ░ĆĻ▓® ļĢīļ¼ĖņŚÉ ļ░▒ĻĖł ņ┤ēļ¦żļ¦īĒü╝ ņÜ░ņłśĒĢ£ ņä▒ļŖźņØä ļ│┤ņØ┤ļ®┤ņä£ Ļ░ĆĻ▓®ņØ┤ ņĀĆļĀ┤ĒĢ£ ļīĆņ▓┤ ņ┤ēļ¦żļź╝ ņ░ŠĻĖ░ ņ£äĒĢ£ ņŚ░ĻĄ¼ļōżņØ┤ ņ¦äĒ¢ēļÉśņ¢┤ ņÖöļŗż. Norskov et al. (2004)[6]ņØĆ DFT Ļ│äņé░ņØä ĒåĄĒĢ┤ ORR ņ┤ēļ¦ż ĒÖ£ņä▒ņØ┤ ļ░śņØæņżæĻ░äņ▓┤ņØś ĒØĪņ░®ņŚÉļäłņ¦ĆņÖĆ ņ¦üņĀæņĀüņØĖ Ļ┤ĆļĀ©ņØ┤ ņ׳ļŗżļŖö Ļ▓āņØä ļ│┤ņŚ¼ņŻ╝ņŚłļŗż. ļ░śņØæņżæĻ░äņ▓┤ ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś ņäĀĒśĢĻ┤ĆĻ│ä [Fig 3b]ļĪ£ ņØĖĒĢ┤ ņ┤ēļ¦żņØś ĒÖ£ņä▒Ļ│╝ ĒØĪņ░®ņŚÉļäłņ¦Ć (Ō¢│G(OHŌłŚ))ļŖö ĒÖöņé░ ļ¬©ņ¢æņØś Ļ┤ĆĻ│äļź╝ ĒśĢņä▒ (Volcano ĻĘĖļלĒöä, [Fig 4a])ĒĢśļŖöļŹ░, ņØ┤ļŖö ņ┤ēļ¦ż ĒÖ£ņä▒ņØä ĻĘ╣ļīĆĒÖöĒĢśĻĖ░ ņ£äĒĢ┤ ĒØĪņ░®ņŚÉļäłņ¦ĆļŖö ļäłļ¼┤ Ļ░ĢĒĢśņ¦ĆļÅä ņĢĮĒĢśņ¦ĆļÅä ņĢŖļŖö ņĄ£ņĀüņØś Ļ░ĢļÅäļź╝ Ļ░¢Ļ│Ā ņ׳ņ¢┤ņĢ╝ĒĢ©ņØä ņØśļ»ĖĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ Ļ┤ĆĻ│äļź╝ ņØ┤ņÜ®ĒĢ┤, ļŗżņ¢æĒĢ£ ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ Ō¢│G(OHŌłŚ)ļź╝ Ļ│äņé░ĒĢ©ņ£╝ļĪ£ņŹ© ņ┤ēļ¦żņØś ĒÖ£ņä▒ņØä ņēĮĻ▓ī ņśłņĖĪĒĢĀ ņłś ņ׳ņ¢┤ ņāłļĪ£ņÜ┤ ņ┤ēļ¦żļź╝ ņĀ£ņĢłĒĢĀ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤ Stamenkovic et al. (2006)[7]ņØĆ ļ░▒ĻĖł ĻĖ░ļ░ś ĒĢ®ĻĖłņŚÉ ļīĆĒĢ£ Ļ│äņé░ Ļ▓░Ļ│╝, ņĄ£ņĀüņØś ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ Ļ░¢ļŖö ņ┤ēļ¦ż (Pt3 Ni, Pt3 Co)ļź╝ Ļ│äņé░ĒÖöĒĢÖņĀüņ£╝ļĪ£ ņĀ£ņĢłĒĢśņśĆĻ│Ā ņŗżĒŚśņ£╝ļĪ£ Ļ▓Ćņ”ØĒĢśņśĆļŗż. ņØ┤ ļ░¢ņŚÉļÅä, ņĮöņ¢┤/ņēś ĻĄ¼ņĪ░ ĒśĢĒā£ņØś ļéśļģĖ ņ×ģņ×É[8] Ēś╣ņØĆ ņŖżĒö╝ļä¼ ņé░ĒÖöļ¼╝[9, 10] ļō▒ ļŗżņ¢æĒĢ£ ĒśĢĒā£ņØś ORR ņ┤ēļ¦żĻ░Ć ņŚ░ĻĄ¼ļÉśĻ│Ā ņ׳ļŗż[11, 12].
Fig.┬Ā3.
a) 4e-ORRņÖĆ 2e-ORR ļ░śņØæ Ļ▓ĮļĪ£. Adapted with permission from Siahrostami et al. 2020;10.14;7495-511. Copyright 2020 American Chemical Society b) ĻĖłņåŹ ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ ļ░śņØæ ņżæĻ░äņ▓┤ ĒØĪņ░®ņŚÉļäłņ¦ĆĻ░äņØś ņäĀĒśĢ Ļ┤ĆĻ│ä. Adapted with permission from Kulkani et al. 2018;118;2032 Copyright 2018 American Chemical Society.
ņäĀĒśĢĻ┤ĆĻ│ä ĻĖ░ļ░śņØś Volcano PlotņØĆ ņāłļĪ£ņÜ┤ ņ┤ēļ¦żļź╝ ĒāÉņāēĒĢśļŖöļŹ░ ļÅäņøĆņØä ņŻ╝ņ¦Ćļ¦ī ņśłņĖĪĒĢśļŖö ņĄ£Ļ│Ā ņä▒ļŖźņØä ņĀ£ĒĢ£ĒĢ£ļŗżļŖö ĒĢ£Ļ│äĻ░Ć ņ׳ļŗż. [Fig 4b]ļŖö ļŗżņ¢æĒĢ£ ņ┤ēļ¦żļōżņØś ņØ┤ļĪĀņĀü ĒÖ£ņä▒ņØä OHŌłŚņÖĆ OOHŌłŚņØś ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņØ┤ņÜ®ĒĢ┤ Ēæ£ĻĖ░ĒĢ£ 2ņ░©ņøÉ Volcano ĻĘĖļלĒöäņØ┤ļŗż. ļ╣©Ļ░äņāē ļČĆļČäņØ┤ ņØ┤ļĪĀņĀüņ£╝ļĪ£ ļŗ¼ņä▒ĒĢĀ ņłś ņ׳ļŖö ņĄ£Ļ│ĀņØś ĒÖ£ņä▒ņØ┤ņ¦Ćļ¦ī ņäĀĒśĢĻ┤ĆĻ│äļź╝ ļö░ļź┤ļŖö ņ┤ēļ¦żļź╝ ĒāÉņāēĒĢ£ļŗżļ®┤ ĒĢ┤ļŗ╣ ĒżņØĖĒŖĖņŚÉ ņĀæĻĘ╝ĒĢĀ ņłś ņŚåļŗż. ļö░ļØ╝ņä£ ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś ņäĀĒśĢĻ┤ĆĻ│äļź╝ Ļ╣©ļŖö Ļ▓āņØ┤ ĒśüņŗĀņĀüņØĖ ORR ņ┤ēļ¦ż Ļ░£ļ░£ņØś ņČ£ļ░£ņĀÉņØ┤ļ®░, ļŗżņ¢æĒĢ£ ļ░®ļ▓ĢļōżņØ┤ ņĀ£ņŗ£ļÉśņ¢┤ ņÖöļŗż. ņśłļź╝ ļōżņ¢┤, Deng et al. (2020)[13]ņØĆ h-BN ņ£äņŚÉ ņ£ĀņŚ░ĒĢ£ ļéśļģĖĒü┤ļ¤¼ņŖżĒä░ļź╝ ņ”Øņ░®ņŗ£ņ╝£ ļ░śņØæņżæĻ░äņ▓┤ļ¦łļŗż ĒØĪņ░®ņäĖĻĖ░Ļ░Ć ļŗżļź┤Ļ▓ī ļ│ĆĒĢśļŖö ņĀÉņØä ņØ┤ņÜ®ĒĢśņśĆĻ│Ā, Fu et al. (2021)[14]ņØĆ ļŗ©ņøÉņ×É ņ┤ēļ¦żņØś ĒØĪņ░®ņ×Éļ”¼ ĻĘ╝ņ▓śņŚÉ ņé░ņåīļź╝ ļÅäĒĢæņŗ£ņ╝£ ĒŖ╣ņĀĢ ļ░śņØæņżæĻ░äņ▓┤ņŚÉļ¦ī ļ░śļ░£ļĀźņØä Ļ░ĆĒĢ┤ ņäĀĒśĢĻ┤ĆĻ│äņŚÉņä£ ļ▓Śņ¢┤ļé£ ļ░ö ņ׳ļŗż.
Fig.┬Ā4.
a) ļŗżņ¢æĒĢ£ ņ┤ēļ¦żņØś ORR ĒÖ£ņä▒ņØä OHŌłŚ ĒØĪņ░®ņŚÉļäłņ¦Ć ļīĆļ╣ä Ēæ£ĻĖ░ĒĢ£ Volcano ĻĘĖļלĒöä. Adapted from Wang et al. SmartMat. 2021;2.1;56-75. b) ļŗżņ¢æĒĢ£ ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ OHŌłŚņÖĆ OOHŌłŚ ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņØ┤ņÜ®ĒĢ┤ ļéśĒāĆļéĖ 2ņ░©ņøÉ Volcano ĻĘĖļלĒöä. ļīĆļČĆļČäņØś ņ┤ēļ¦żņŚÉņä£ ļ░śņØæņżæĻ░äņ▓┤ņØś ĒØĪņ░®ņŚÉļäłņ¦ĆĻ░Ć ņäĀĒśĢ Ļ┤ĆĻ│äļź╝ ļ│┤ņØ┤Ļ│Ā ņ׳ļŗż. Adapted with permission from Kulkani et al. 2018;118;2032 Copyright 2018 American Chemical Society.
2.2 ņé░ņåīļ░£ņāØ ļ░śņØæ (Oxygen Evolution Reaction, OER)
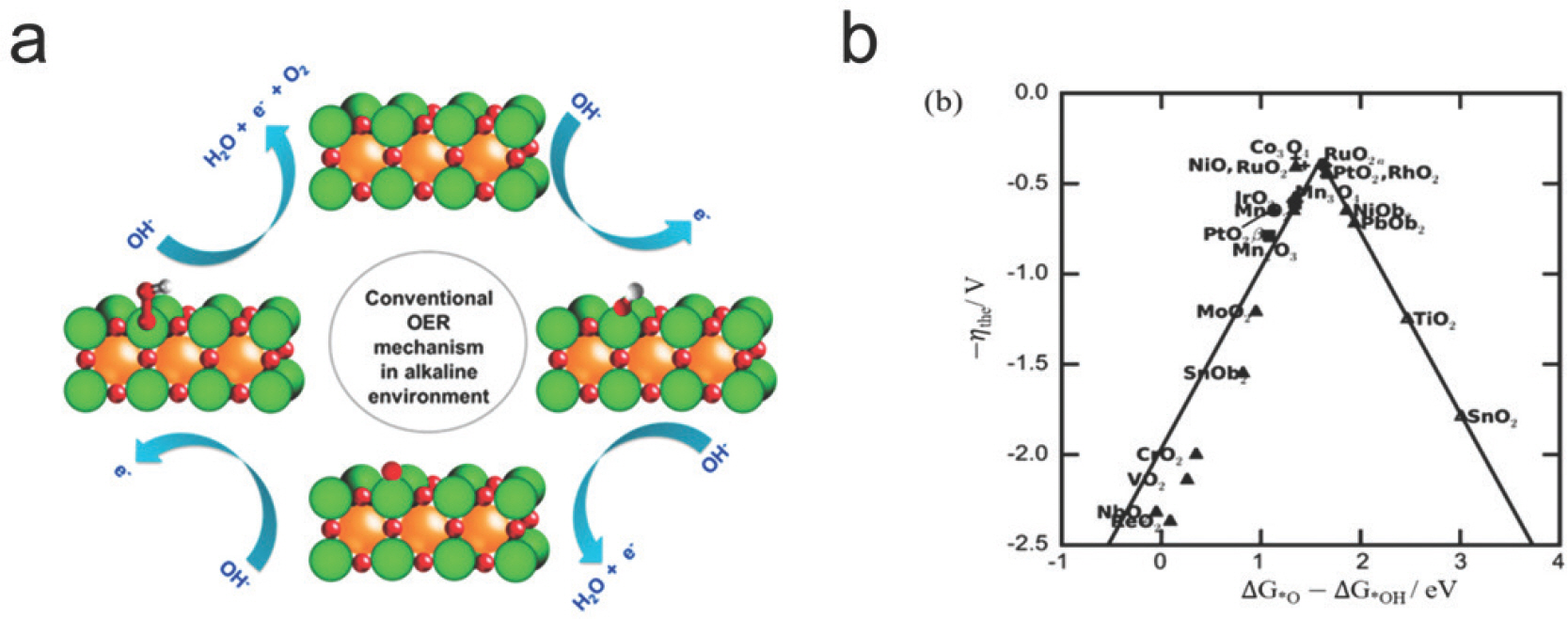
OERņØĆ ĻĘĖļ”░ ņłśņåī ņāØņé░ņØä ņ£äĒĢ£ ņłśņĀäĒĢ┤ņØś ņØīĻĘ╣ ļ░śņØæņ£╝ļĪ£ ļ¼╝ ļČäņ×ÉĻ░Ć ņé░ĒÖöļÉśņ¢┤ ņé░ņåīļź╝ ļ░£ņāØĒĢśļŖö ļ░śņØæņØ┤ļ®░, ORR ļ░śņØæņØś ņŚŁļ░śņØæņØ┤ļŗż (ņŗØ3). OERņØĆ ORRĻ│╝ ļ¦łņ░¼Ļ░Ćņ¦ĆļĪ£ 4ļŗ©Ļ│äļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ļ░śņØæņØ┤Ļ│Ā 3Ļ░£ņØś ļ░śņØæņżæĻ░äņ▓┤ (OŌłŚ, OHŌłŚ, ĻĘĖļ”¼Ļ│Ā OOHŌłŚ)Ļ░Ć ņ░ĖņŚ¼ĒĢ£ļŗż [Fig 5a] (ņŗØ4). ļŗżņ¢æĒĢ£ ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ OHŌłŚņÖĆ OOHŌłŚņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ņ░©ņØ┤Ļ░Ć ņØ╝ņĀĢĒĢśļŗżĻ│Ā ņĢīļĀżņĀĖ ņ׳Ļ│Ā (Ō¢│G(OOHŌłŚ)=Ō¢│ G(OHŌłŚ)+3.2 eV), ņØ┤ļĪ£ ņØĖĒĢ┤ ļÅäļŗ¼ Ļ░ĆļŖźĒĢ£ ņĄ£ņåī Ļ│╝ņĀäņĢĢņØĆ 0.37 VļĪ£ ņĢīļĀżņĀĖ ņ׳ļŗż (=3.2 eV/2e ŌłÆ1.23 V). ņØ┤ļ¤¼ĒĢ£ Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ OER ĒÖ£ņä▒ņØä Ļ▓░ņĀĢĒĢśļŖö ņØĖņ×ÉļĪ£ OŌłŚņÖĆ OHŌłŚ ĒØĪņ░®ņŚÉļäłņ¦Ć ņ░©ņØ┤ņØĖ Ō¢│G(OŌłŚ)-Ō¢│G(OHŌłŚ)Ļ░Ć ņĀ£ņĢłļÉśņŚłļŗż[15]. [Fig 5b]ļŖö ļŗżņ¢æĒĢ£ ņĀäņØ┤ĻĖłņåŹ ņé░ĒÖöļ¼╝ņØś OER ĒÖ£ņä▒ņØä Ō¢│G(OŌłŚ)-Ō¢│G(OHŌłŚ)ņŚÉ ļīĆĒĢ┤ ļéśĒāĆļéĖ Volcano ĻĘĖļלĒöäņØ┤Ļ│Ā, ņŻ╝ļĪ£ IrO2ņÖĆ RuO2 Ļ░ÖņØĆ ĻĘĆĻĖłņåŹ ņé░ĒÖöļ¼╝ņØ┤ ļåÆņØĆ ĒÖ£ņä▒ņØä ļ│┤ņŚ¼ņżĆļŗż. Volcano ĻĘĖļלĒöäļź╝ ļ░öĒāĢņ£╝ļĪ£ ņĀüņĀłĒĢ£ Ō¢│G(OŌłŚ)-Ō¢│G(OHŌłŚ)ļź╝ Ļ░¢ļŖö ņ┤ēļ¦żļź╝ ņäżĻ│äĒĢśĻĖ░ ņ£äĒĢ┤ ļŗżņ¢æĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ņłśĒ¢ēļÉśņŚłļŗż. Xue et al. (2019)[16]ņØĆ ļŗłņ╝ł ņłśņé░ĒÖöļ¼╝ņŚÉ ļŗżņ¢æĒĢ£ ņĀäņØ┤ĻĖłņåŹņØä ļÅäĒĢæņŗ£ņ╝£ OER ņä▒ļŖźņØä ĒÅēĻ░ĆĒĢśņśĆņ£╝ļ®░, Fe ļÅäĒĢæņŗ£ RuO2ņÖĆ IrO2 ļ│┤ļŗż Ēø©ņö¼ ļé«ņØĆ Ļ│╝ņĀäņĢĢ (0.21 V)ņØä Ļ░¢ļŖö Ļ▓āņØä ļ│┤Ļ│ĀĒĢśņśĆļŗż. Yang et al. (2022)ņØĆ ĻĘĖļלĒĢĆ(pyridine/amino-nitrogen decorated)ņŚÉ 2Ļ░£ņØś ļŗżņ¢æĒĢ£ ņĀäņØ┤ĻĖłņåŹņØä ļÅäĒĢæĒĢśņśĆņØä ļĢīņØś OER ĒÖ£ņä▒ņØä ņŖżĒü¼ļ”¼ļŗØ ĒĢśņśĆņ£╝ļ®░, CoņÖĆ Niļź╝ ļÅÖņŗ£ņŚÉ ļÅäĒĢæĒĢśņśĆņØä ļĢī 0.31 eVņØś Ļ│╝ņĀäņĢĢņØä Ļ░¢ļŖö Ļ▓āņØä ļ│┤Ļ│ĀĒĢśņśĆļŗż[17]. ņØ┤ ņÖĖņŚÉļÅä, ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ļō£ ņé░ĒÖöļ¼╝[18], ļéśļģĖņ×ģņ×É[19, 20]ņÖĆ Ļ░ÖņØ┤ ļŗżņ¢æĒĢ£ ĒśĢĒā£ņØś ļ¼╝ņ¦łļōżņØ┤ OER ņ┤ēļ¦żļĪ£ ļ│┤Ļ│ĀļÉ£ ļ░ö ņ׳ļŗż.
Fig.┬Ā5.
a) OER ļ░śņØæ Ļ▓ĮļĪ£. Adapted with permission from Fabbri et al. 2018;8.10;9765-74 Copyright 2018 American Chemical Society. b) ļŗżņ¢æĒĢ£ ņĀäņØ┤ĻĖłņåŹ ņé░ĒÖöļ¼╝ņØś OER ĒÖ£ņä▒ņØä Ō¢│G(OŌłŚ)-Ō¢│G(OHŌłŚ)ņŚÉ ļīĆĒĢ┤ ļéśĒāĆļéĖ Volcano ĻĘĖļלĒöä. Adapted from Man et al. ChemCatChem 2011;3.7;1159-1165, with permission of Wiley
2.3 ĒÜ©ņ£©ņĀüņØĖ ĒØĪņ░®ņŚÉļäłņ¦Ć ņśłņĖĪņØä ņ£äĒĢ£ ņĀæĻĘ╝ļ▓ĢĻ│╝ ĻĘĖ ĒĢ£Ļ│ä
[Fig 3~5]ņŚÉ ļéśĒāĆļé£ Ļ▓āĻ│╝ Ļ░ÖņØ┤ ĒØĪņ░®ņŚÉļäłņ¦ĆļŖö ņ┤ēļ¦żņØś ĒÖ£ņä▒ņØä ņśłņĖĪĒĢśļŖöļŹ░ ņé¼ņÜ®ļÉśļŖö ņŻ╝ņÜö ņØĖņ×ÉņØ┤ļ®░, ņāłļĪ£ņÜ┤ ņ┤ēļ¦żņŚÉ ļīĆĒĢ£ ņä▒ļŖź ĒÅēĻ░Ćļź╝ ņ£äĒĢ┤ ņłś ļ¦ÄņØĆ ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ Ļ│äņé░ĒĢ┤ņĢ╝ ĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī ļŗżņ¢æĒĢ£ ņĪ░ĒĢ®ņØś ļ¼╝ņ¦ł ļ░Å Ēæ£ļ®┤ņØä Ļ│ĀļĀżĒĢ┤ņĢ╝ ĒĢśĻ│Ā, Ļ░üĻ░üņØś DFT Ļ│äņé░ņŚÉ ņåīņÜöļÉśļŖö ņŗ£Ļ░äņØ┤ ņāüļŗ╣ĒĢśļŗż. ņØ┤ļź╝ ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ┤ ĒØĪņ░®ņŚÉļäłņ¦ĆņÖĆ ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ Ļ░Ćņ¦Ćļ®┤ņä£ ņĀüņØĆ DFT Ļ│äņé░ņ£╝ļĪ£ ņ¢╗ņØä ņłś ņ׳ļŖö ĒŖ╣ņä▒ņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£Ē׳ ņ¦äĒ¢ēļÉśņŚłļŗż.
ņ┤ēļ¦ż Ēæ£ļ®┤ņØś d-band centerĻ░Ć ļīĆĒæ£ņĀüņØĖ ņśłņØ┤ļŗż. 2000ļģäļÅä B. HammerņÖĆ J.K. NorskŌŖśvļŖö d-band ņØ┤ļĪĀņØä ņĀ£ņĢłĒĢśņŚ¼ ĻĖłņåŹ ļ░Å ĒĢ®ĻĖł Ēæ£ļ®┤ņŚÉņä£ ļåÆņØĆ d-band centerļź╝ Ļ░¢ļŖö Ļ▓ĮņÜ░ antibonding stateņŚÉ ņĀäņ×ÉĻ░Ć ņ▒äņøīņ¦ł ĒÖĢļźĀņØ┤ ļé«Ļ│Ā, ĻĘĖ Ļ▓░Ļ│╝ ĒØĪņ░®ļ¼╝Ļ│╝ ņāüĒśĖņ×æņÜ®ņØ┤ Ļ░ĢĒĢśļŗżļŖö Ļ▓āņØä ļ│┤ņśĆļŗż. d-band centerņÖĆ ĒØĪņ░®ņŚÉļäłņ¦ĆņØś ņäĀĒśĢ Ļ┤ĆĻ│äļź╝ ļŗżņ¢æĒĢ£ ņ┤ēļ¦żņŚÉ ļīĆĒĢ┤ ņĀüņÜ®ĒĢ┤ ņŗĀ ņ┤ēļ¦ż ņäżĻ│äņŚÉ Ēü░ ĻĖ░ņŚ¼ļź╝ ĒĢśņśĆļŗż.[21] [Fig 6a] ņØ┤ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Chen et al. (2014)ņØĆ Pt3 M (111) ĒĢ®ĻĖł Ēæ£ļ®┤ņŚÉņä£ ļŗżņ¢æĒĢ£ ĒØĪņ░®ļ¼╝ņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ļČäņäØņØä ņ¦äĒ¢ēĒĢśņśĆņ£╝ļ®░, d-band centerņÖĆ ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś ņäĀĒśĢĻ┤ĆĻ│äļź╝ ļ░öĒāĢņ£╝ļĪ£ ņŗĀņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ ņä▒Ļ│ĄĒĢśņśĆļŗż[22]. [Fig 6b].
Fig.┬Ā6.
a) ņĀäņØ┤ĻĖłņåŹĻ│╝ ĒØĪņ░®ļ¼╝ņØś Ļ▓░ĒĢ®ņØ┤ ĒśĢņä▒ļÉśļŖö Ļ│╝ņĀĢņŚÉ ļīĆĒĢ£ ņŚÉļäłņ¦Ć ļÅäĒæ£. Adapted from Bhattacharjee et al. Sci. Rep. 2016;6.1;1-10. b) Pt3M(111) ņĀäņØ┤ĻĖłņåŹ ĒĢ®ĻĖł ņ┤ēļ¦żņØś d-band centersņÖĆ ļŗżņ¢æĒĢ£ ĒØĪņ░®ļ¼╝ņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ņé¼ņØ┤ņØś ņāüĻ┤ĆĻ┤ĆĻ│ä. Adapted with permission from Chen et al. J. Phys. Chem. C 2014;118.16;8342-49 Copyright 2014 American Chemical Society.

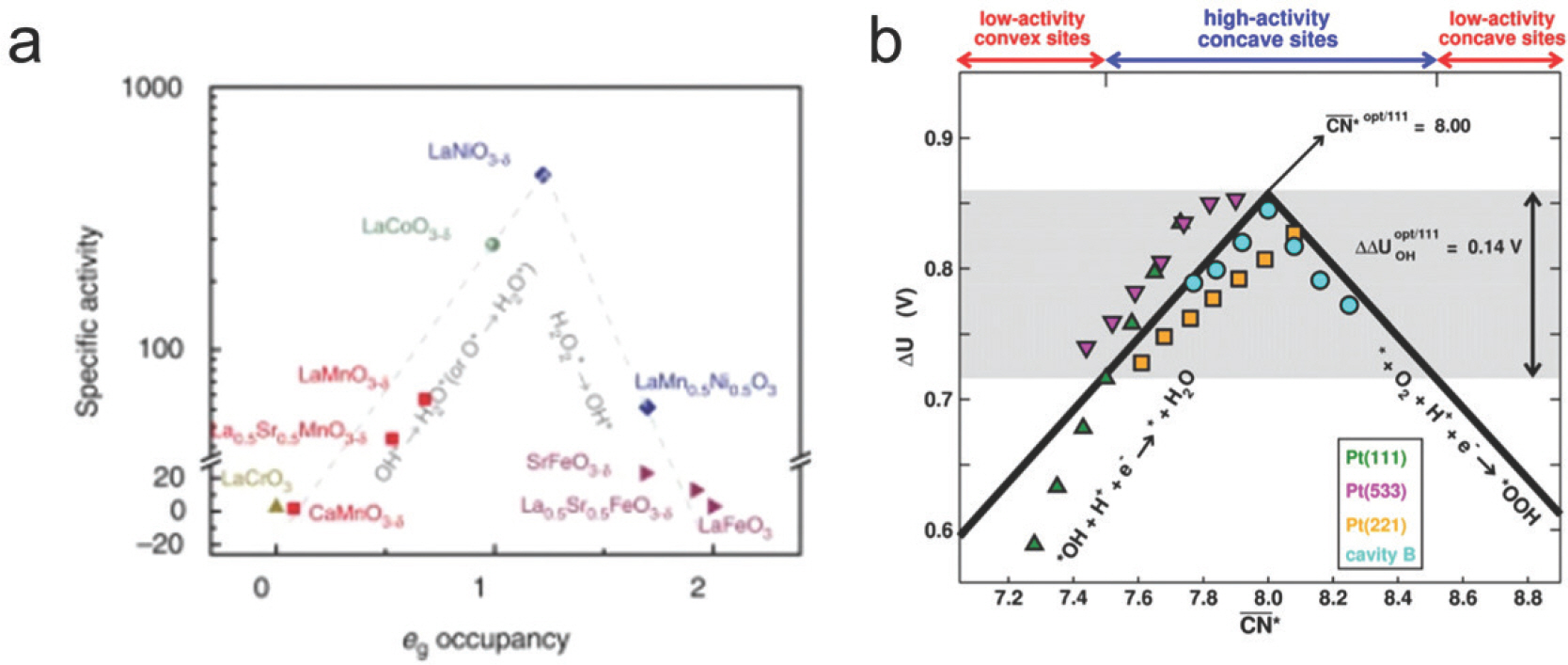
d-band modelņØä ņŗ£ņ×æņ£╝ļĪ£ ņĀäņ×ÉĻĄ¼ņĪ░ņÖĆ ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś ņŚ░Ļ┤Ćņä▒ņØä ļŗżņ¢æĒĢ£ Ļ┤ĆņĀÉņŚÉņä£ ņé┤ĒÄ┤ļ│┤ļŖö ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£ĒĢśĻ▓ī ņØ┤ņ¢┤ņĪīļŗż. ņśłļź╝ ļōżņ¢┤ Dickens et al. (2019)ņØĆ DFT Ļ│äņé░ņØä ĒåĄĒĢ┤ ņé░ņåī ĒØĪņ░®ļ¼╝ņØś ĒØĪņ░®ņäĖĻĖ░ņÖĆ ĒÅēĻĘĀ 2p state ņŚÉļäłņ¦ĆņØś Ļ┤ĆĻ│äļź╝ ļ░£Ļ▓¼ĒĢśņśĆĻ│Ā, ļŗżņ¢æĒĢ£ ĻĖłņåŹ ļ░Å ĻĖłņåŹ ņé░ĒÖöļ¼╝ņŚÉņä£ ņé░ņåī ĒØĪņ░®ļ¼╝ (OŌłŚ)ņØś 2p state ņŚÉļäłņ¦Ćļź╝ OER ĒÖ£ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉļĪ£ ņĀ£ņŗ£ĒĢśņśĆļŗż[23]. ļśÉĒĢ£ Wang et al. (2019)ņØĆ ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖ (ABO3)ņØś B ĻĖłņåŹņØś e g ņśżļ╣äĒāłņØś ņĀäņ×É Ļ░£ņłśļź╝ OER ĒÖ£ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉļĪ£ ņĀ£ņŗ£ĒĢśņśĆļŗż[24] [Fig 7a]. Ēæ£ļ®┤ ĻĄ¼ņĪ░ ņĀĢļ│┤ņÖĆ ĒØĪņ░®ņŚÉļäłņ¦ĆņØś ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ ļ░£Ļ▓¼ĒĢ£ Ļ▓░Ļ│╝ļÅä ļ│┤Ļ│ĀļÉśņŚłļŗż. Calle-Vallejo et al. (2018)ņØĆ PtņÖĆ AuņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ļČäņäØņØä ĒåĄĒĢ┤ ņ┤ēļ¦żņØś Ļ▓®ņ×Éļ│ĆĒśĢ ĒÜ©Ļ│╝ (Strain Effect)ļź╝ ņØ╝ļ░śĒÖöļÉ£ ļ░░ņ£ä ņłś (Generalized Coordination Number)ļź╝ ņØ┤ņÜ®ĒĢ┤ ņäżļ¬ģĒĢśņśĆĻ│Ā, ņØ┤ļź╝ ORR ĒÖ£ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉļĪ£ ņĀ£ņŗ£ĒĢśņśĆļŗż[25] [Fig 7b]. ņØ┤ ņÖĖņŚÉļÅä ļ▓ĀņØ┤ļŹö ņĀäĒĢś (Bader Charge), ņŖżĒĢĆ ļ¬©ļ®śĒŖĖ (Spin Moment)[26]ņÖĆ Ļ░ÖņØĆ ĒŖ╣ņä▒ļōżļÅä ņ┤ēļ¦ż ĒÖ£ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉļĪ£ ņĀ£ņŗ£ļÉśņŚłļŗż.
Fig.┬Ā7.
a) ABO3 ĒÄśļĪ£ļĖīņŖżņ╣┤ņØ┤ĒŖĖņØś B site ĻĖłņåŹņØś e g ņĀäņ×ÉņÖĆ OER ĒÖ£ņä▒ņØś Ļ┤ĆĻ│äļź╝ ļ│┤ņŚ¼ņŻ╝ļŖö Volcano ĻĘĖļלĒöä. Adapted from Wang et al. Nat. Commun. 2019;10.1;1-8. b) PtņŚÉņä£ ļ░░ņ£ä ņłśņÖĆ ORR ĒÖ£ņä▒ņØś Ļ┤ĆĻ│äļź╝ Ēæ£ĻĖ░ĒĢ£ ĻĘĖļלĒöä. Adapted from Calle-Vallejo et al. ChemSusChem 2018;11;5, with permission of Wiley
ņØ┤ņÖĆ Ļ░ÖņØ┤ ņ┤ēļ¦ż Ēæ£ļ®┤ņØś ņĀäņ×ÉĻĄ¼ņĪ░ ņĀĢļ│┤ņÖĆ ĻĄ¼ņĪ░ņĀü ĒŖ╣ņä▒ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ┤ēļ¦ż ĒÖ£ņä▒ņØä ņäżļ¬ģĒĢśĻĖ░ ņ£äĒĢ£ ņłśļ¦ÄņØĆ ņŗ£ļÅäļōżņØ┤ ņ׳ņŚłņ£╝ļéś ņ┤ēļ¦ż ņä▒ļŖźņØä ĒÅēĻ░ĆĒĢśļŖöļŹ░ ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŖö ļ▓öņÜ®ņĀüņØ┤Ļ│Ā ļåÆņØĆ ņĀĢĒÖĢļÅäņØś ĒÖ£ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉļŖö Ēśäņ×¼Ļ╣īņ¦Ć ļ│┤Ļ│ĀļÉśņ¦Ć ņĢŖņĢśļŗż. ņØ┤ļŖö ņ┤ēļ¦żņØś ļŗżņ¢æĒĢ£ ĒÖöĒĢÖņĀü, ļ¼╝ļ”¼ņĀü ĒŖ╣ņä▒Ļ│╝ ņĀäņ×É ĻĄ¼ņĪ░ ņĀĢļ│┤ņØś ņāüĻ┤Ć Ļ┤ĆĻ│äļź╝ ļ░ØĒ׳ļŖöļŹ░ ļ¦ÄņØĆ ņŗ£Ļ░äņØ┤ ņåīļ¬©ļÉśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ļśÉĒĢ£ DFT Ļ│äņé░ņØĆ ĻĄ¼ņĪ░Ļ░Ć ļ│Ąņ×Ī, ļŗżņ¢æĒĢ┤ņ¦łņłśļĪØ ņåīļ¬©ļÉśļŖö Ļ│äņé░ ļ╣äņÜ®ņØ┤ ļ¦żņÜ░ ņ╗żņ¦ĆĻĖ░ ļĢīļ¼ĖņŚÉ, ļäōņØĆ ĒÖöĒĢÖĻ│ĄĻ░äņŚÉņä£ ņøÉĒĢśļŖö ĒŖ╣ņä▒ņØä ļ¦īņĪ▒ĒĢśļŖö ņ┤ēļ¦żļź╝ ņ░ŠĻĖ░ ņ£äĒĢ┤ Ļ░äļŗ©ĒĢ£ DFT Ļ│äņé░ņ£╝ļĪ£ ĻĄ¼ĒĢĀ ņłś ņ׳ļŖö ĒŖ╣ņä▒ņØä ĒÖ£ņÜ®ĒĢśņŚ¼ ĒÖ£ņä▒ņØä ņśłņĖĪĒĢĀ ĒĢäņÜöĻ░Ć ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĒĢ£Ļ│äļź╝ ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢ┤ ņĄ£ĻĘ╝ņŚÉļŖö ļ╣ģļŹ░ņØ┤Ēä░ļĪ£ļČĆĒä░ ņ×ģļĀźĻ░Æ (Input Value)Ļ│╝ ļ¬®Ēæ£Ļ░Æ (Target Value)ņØś Ļ┤ĆĻ│äļź╝ ņŖżņŖżļĪ£ ĒĢÖņŖĄĒĢśĻ│Ā, ņŻ╝ņ¢┤ņ¦ä ņ×ģļĀźĻ░ÆņŚÉ ļīĆĒĢ£ ļ¬®Ēæ£Ļ░ÆņØä ļåÆņØĆ ņĀĢĒÖĢļÅäļĪ£ ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ĻĖ░Ļ│äĒĢÖņŖĄņØä ĒÖ£ņÜ®ĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£Ē׳ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż. 3ņĀłņŚÉņä£ļŖö ĻĖ░Ļ│äĒĢÖņŖĄņØ┤ Ļ│äņé░ĒÖöĒĢÖĻ│╝ ĒĢ©Ļ╗ś ņ┤ēļ¦ż Ļ░£ļ░£ ļČäņĢ╝ņŚÉņä£ ņ¢┤ļ¢╗Ļ▓ī ņé¼ņÜ®ļÉśļŖöņ¦Ć ņåīĻ░£ĒĢśĻ│Āņ×É ĒĢ£ļŗż.
3. ĻĖ░Ļ│äĒĢÖņŖĄņØä ņØ┤ņÜ®ĒĢ£ ņ┤ēļ¦ż Ļ░£ļ░£ ņŚ░ĻĄ¼
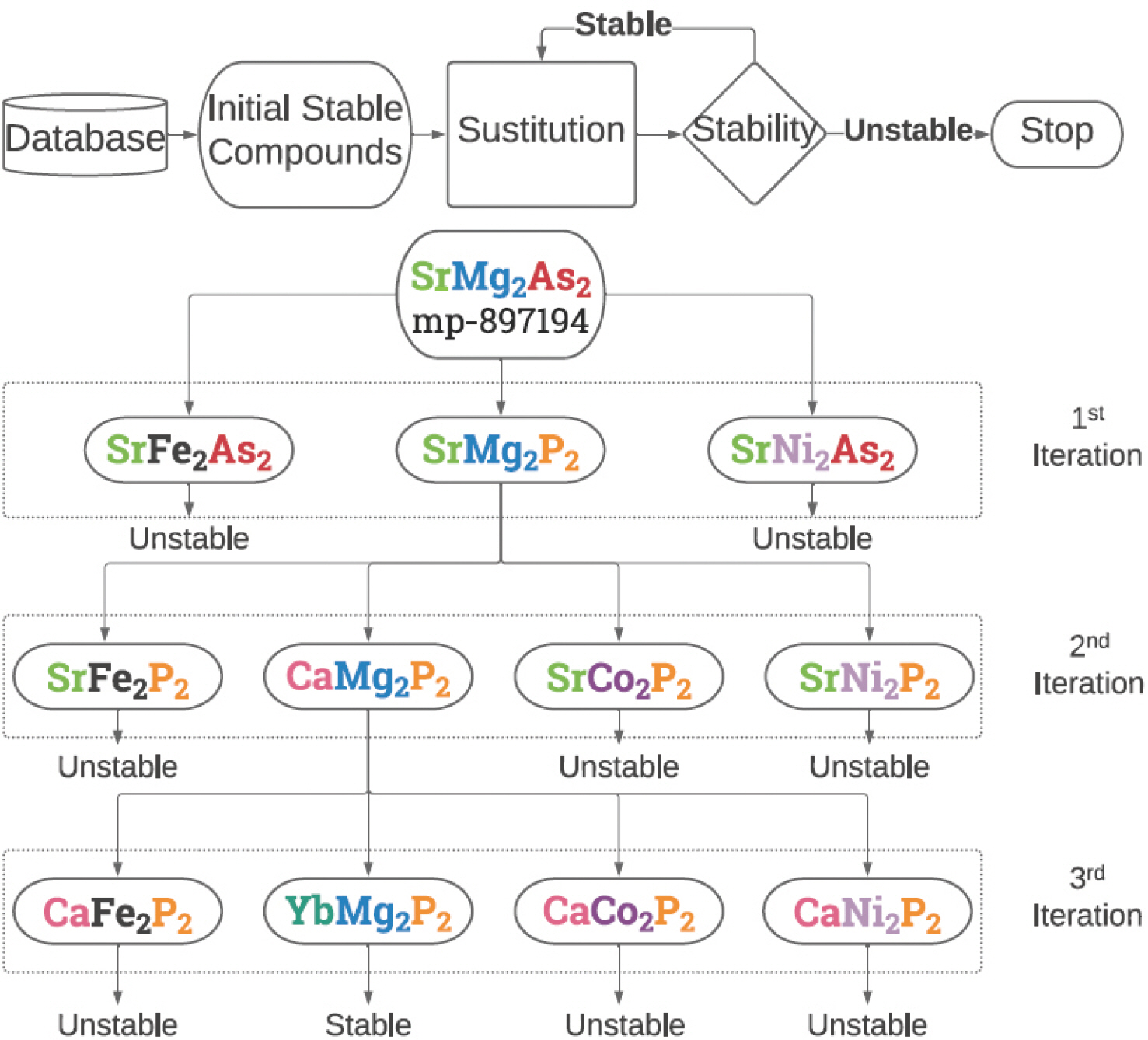
ņĄ£ĻĘ╝ ĻĖ░Ļ│äĒĢÖņŖĄņØĆ ļŗżņ¢æĒĢ£ ļČäņĢ╝ņŚÉņä£ ĒÖ£ņÜ®ļÉśĻ│Ā ņ׳ļŗż. ĻĖ░Ļ│äĒĢÖņŖĄņØĆ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļĪ£ļČĆĒä░ ņĀĢļ│┤ļź╝ ņČöņČ£ĒĢśņŚ¼ ņāüĻ┤Ć Ļ┤ĆĻ│äļź╝ ļČäņäØĒĢśĻĖ░ ņ£äĒĢ£ ņ£ĀņÜ®ĒĢ£ ļÅäĻĄ¼ņØ┤ļ®░, Ļ│äņé░ĒÖöĒĢÖ ļČäņĢ╝ņŚÉņä£ļŖö ļŹ░ņØ┤Ēä░ņØś ņČĢņĀüĻ│╝ ņāłļĪ£ņÜ┤ ņĢīĻ│Āļ”¼ņ”śņØś Ļ░£ļ░£ļĪ£ ĻĖ░Ļ│äĒĢÖņŖĄņØä ĒÖ£ņÜ®ĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ņĀÉņĀÉ ņ”ØĻ░ĆĒĢśĻ│Ā ņ׳ļŗż [Fig 2].
ņØ╝ļ░śņĀüņØĖ ļČäņĢ╝ņŚÉņä£ ĻĖ░Ļ│äĒĢÖņŖĄ ļČäļźśņÖĆ ņ£Āņé¼ĒĢśĻ▓ī ņ┤ēļ¦ż ļ░Å Ļ│äņé░ĒÖöĒĢÖ ļČäņĢ╝ņŚÉņä£ļÅä Ļ░üĻ░üņØś ļ¬®ņĀüņŚÉ ļ¦×Ļ▓ī ņ¦ĆļÅäĒĢÖņŖĄĻ│╝ ļ╣äņ¦ĆļÅäĒĢÖņŖĄņØä ņé¼ņÜ®ĒĢśĻ│Ā ņ׳ļŗż. ņ¦ĆļÅäĒĢÖņŖĄņØĆ ņ┤ēļ¦żņØś ņ×ģļĀź ĒŖ╣ņä▒ (Input Feature)ņŚÉ ļīĆņØæĒĢśļŖö ļ¬®Ēæ£Ļ░ÆņØä ļØ╝ļ▓©ļ¦üĒĢśņŚ¼ ĒĢÖņŖĄņŗ£Ēéżļ®░, ņŻ╝ņ¢┤ņ¦ä ņ×ģļĀź ĒŖ╣ņä▒ņŚÉ ļīĆĒĢ£ ļ¬©ļŹĖņØś ņśłņĖĪĻ░ÆĻ│╝ ņŗżņĀ£Ļ░ÆņØä ļ╣äĻĄÉĒĢśņŚ¼ ļ¬©ļŹĖņØś ņä▒ļŖźņØä ĒÅēĻ░ĆĒĢśĻ│Ā ņĄ£ņĀüĒÖöĒĢ£ļŗż. ļ░śļ®┤, ļ╣äņ¦ĆļÅä ĒĢÖņŖĄņØĆ ļ¬®Ēæ£Ļ░ÆņØ┤ ņŚåļŖö ļŹ░ņØ┤Ēä░ņŚÉ ļīĆĒĢ┤ ņ×ģļĀź ĒŖ╣ņä▒ņØä ļ░öĒāĢņ£╝ļĪ£ Ēī©Ēä┤ņØä ĒīīņĢģĒĢśļ®░, ņØ┤ļź╝ ĒåĄĒĢ┤ ļŹ░ņØ┤Ēä░ņØś ņ£Āņé¼ņä▒ņØä ĒĢÖņŖĄĒĢĀ ņłś ņ׳ļŗż. ļśÉĒĢ£ ņĄ£ĻĘ╝ņŚÉļŖö ĒĢ®ņä▒Ļ│▒ņŗĀĻ▓Įļ¦Ø (Convolutional Neural Network, CNN)Ļ│╝ Ļ░ÖņØĆ ļöźļ¤¼ļŗØ ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢ┤ ļ╣äņ¦üĻ┤ĆņĀüņØĖ ņ×ģļĀź ĒŖ╣ņä▒Ļ│╝ ļ¬®Ēæ£Ļ░ÆņØś ņāüĻ┤ĆĻ┤ĆĻ│äļź╝ ĒĢÖņŖĄĒĢĀ ņłś ņ׳ļŗż.
Ļ│äņé░ĒÖöĒĢÖņØä ņØ┤ņÜ®ĒĢ£ ņ┤ēļ¦ż Ļ░£ļ░£ ļČäņĢ╝ņŚÉņä£ ĻĖ░Ļ│äĒĢÖņŖĄņØĆ ĒĢÖņŖĄņÜ® ļŹ░ņØ┤Ēä░ ĻĄ¼ņČĢ, ņĀüņĀłĒĢ£ ņ×ģļĀź ĒŖ╣ņä▒ ņäĀĒāØ, ļ¬©ļŹĖ Ļ░£ļ░£ņØś ņäĖ ļŗ©Ļ│äļĪ£ ļéśļłī ņłś ņ׳ļŗż. ļ│Ė ņĀłņŚÉņä£ļŖö ņĄ£ĻĘ╝ ņŚ░ĻĄ¼ļź╝ ļ░öĒāĢņ£╝ļĪ£ Ļ░ü ļŗ©Ļ│äņØś ņé¼ļĪĆļź╝ ņé┤ĒÄ┤ļ│┤Ļ│Āņ×É ĒĢ£ļŗż.
3.1 ļŹ░ņØ┤Ēä░ ņāØņä▒
ļåÆņØĆ ņĀĢĒÖĢņä▒ņØś ņ┤ēļ¦ż ĒŖ╣ņä▒ ņśłņĖĪ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśĻĖ░ ņ£äĒĢ┤ ņøÉņ×É ĻĄ¼ņĪ░ņÖĆ ĒĢ┤ļŗ╣ ĻĄ¼ņĪ░ņŚÉ ļīĆĒĢ£ DFT Ļ│äņé░ Ļ▓░Ļ│╝ļź╝ ĒżĒĢ©ĒĢśļŖö ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖż ĻĄ¼ņČĢņØ┤ ĒĢäņłśņĀüņØ┤ļŗż. ņŗ£Ļ░äĻ│╝ ļ╣äņÜ®ņØ┤ ļ¦ÄņØ┤ ņåīļ¬©ļÉśļŖö ņŗżĒŚśņØä ĒåĄĒĢ┤ņä£ ļīĆļ¤ēņØś ļŹ░ņØ┤Ēä░ļź╝ ņāØņä▒ĒĢśĻĖ░ ņ¢┤ļĀĄņ¦Ćļ¦ī, DFTļź╝ ĒåĄĒĢ┤ņä£ ļ╣äĻĄÉņĀü ņĀüņØĆ ļ╣äņÜ®ņ£╝ļĪ£ ļäōņØĆ ļ▓öņ£äņØś ļ¼╝ņ¦łņŚÉ ļīĆĒĢ£ Ļ│äņé░ ļŹ░ņØ┤Ēä░ļź╝ ņāØņä▒ĒĢĀ ņłś ņ׳ļŗż.
ļ¼┤ĻĖ░ ņ┤ēļ¦ż ļČäņĢ╝ņŚÉņä£ ļīĆĒæ£ņĀüņØĖ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļĪ£ļŖö Kirklin et al. (2015)[27]ņØś Open Quantum Materials Database (OQMD)Ļ░Ć ņ׳ļŗż. OQMDļŖö ļ¼┤ĻĖ░ ņ┤ēļ¦żņØś ĻĄ¼ņĪ░ ņĀĢļ│┤ļ¦īņØä ĒżĒĢ©ĒĢśĻ│Ā ņ׳ļŖö Inorganic Crystal Structure Database (ICSD)ļĪ£ļČĆĒä░ ņČöņČ£ĒĢ£ 32,559Ļ░£ņØś ļ¼╝ņ¦łņŚÉ ļīĆĒĢ┤ DFT Ļ│äņé░ņØä ņłśĒ¢ēĒĢśņŚ¼ Ļ░ü Ļ▓░ņĀĢ ĻĄ¼ņĪ░ņØś Ļ░Ćņן ņĢłņĀĢĒĢ£ ņāüĒā£ņŚÉņä£ņØś ņŚÉļäłņ¦Ćļź╝ Ļ│äņé░ĒĢśņŚ¼ ņĀ£Ļ│ĄĒĢśĻ│Ā ņ׳ļŗż. ļśÉĒĢ£ Jain et al. (2013)[28]ņØĆ 2022ļģä 4ņøö Ēśäņ×¼ 144,595Ļ░£ņØś ļ¼┤ĻĖ░ Ļ▓░ņĀĢ ĻĄ¼ņĪ░ņÖĆ 63,876 Ļ░£ņØś ļČäņ×É, 530,243 Ļ░£ņØś Nanoporous ļ¼╝ņ¦łļĪ£ ĻĄ¼ņä▒ļÉ£ Materials Project (MP) ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļź╝ ĻĄ¼ņČĢĒĢśņśĆļŗż. MP ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļŖö ĻŠĖņżĆĒ׳ ņŚģļŹ░ņØ┤ĒŖĖļÉśĻ│Ā ņ׳ņ£╝ļ®░ ĻĄ¼ņĪ░ ņĀĢļ│┤ņÖĆ ņŚÉļäłņ¦Ć ņÖĖņŚÉļÅä ņĀäņ×ÉļØĀ ĻĄ¼ņĪ░ (Electronic Band Structure)ņÖĆ Ļ░ÖņØĆ ņĀäņ×ÉĻĄ¼ņĪ░ ņĀĢļ│┤ļÅä ĒżĒĢ©ļÉśņ¢┤ ņ׳ņ¢┤ ĒĢÖņŖĄņØä ņ£äĒĢ£ ņ×ģļĀź ĒŖ╣ņä▒ ņĀĢļ│┤ļĪ£ ņ£ĀņÜ®ĒĢśĻ▓ī ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż.
ņĄ£ĻĘ╝ Chanussot et al. (2021)[29]ņØĆ ļŗżņ¢æĒĢ£ ņóģļźśņØś ņøÉņåīļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä Ēæ£ļ®┤Ļ│╝ N, C ĻĘĖļ”¼Ļ│Ā Oļź╝ ĒżĒĢ©ĒĢśĻ│Ā ņ׳ļŖö ĒØĪņ░®ļ¼╝ņŚÉ ļīĆĒĢ£ 120ļ¦īĻ░£ņØś DFT Ļ│äņé░ ļŹ░ņØ┤Ēä░ņÖĆ 2ņ¢Ą6000ļ¦īĻ░£ņØś Single-point Ļ│äņé░ Ļ░ÆņØä ĒżĒĢ©ĒĢśĻ│Ā ņ׳ļŖö Open Catalyst 2020 (OC20) ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļź╝ ĻĄ¼ņČĢĒĢśņśĆļŗż. OC20 ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļŖö ņĢ×ņäĀ ļ▓īĒü¼ ĻĄ¼ņĪ░ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżņÖĆ ļŗżļź┤Ļ▓ī ņŻ╝ļĪ£ Ēæ£ļ®┤Ļ│╝ ĒØĪņ░®ņŚÉļäłņ¦Ć ņĀĢļ│┤ļĪ£ ņØ┤ļŻ©ņ¢┤ņĀĖ ņ׳ņ¢┤ ĒÖ£ņä▒ ļ░Å ņäĀĒāØņä▒Ļ│╝ Ļ░ÖņØĆ ņ┤ēļ¦ż ĒŖ╣ņä▒ņØä ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż. ĒĢ┤ļŗ╣ ļģ╝ļ¼ĖņŚÉņä£ļŖö ļ╣ģļŹ░ņØ┤Ēä░ņÖĆ ĻĖ░Ļ│äĒĢÖņŖĄ ĻĖ░ļ░ś ņ┤ēļ¦ż ņäżĻ│äļź╝ ņ£äĒĢ┤ ĒĢ┤Ļ▓░ĒĢ┤ņĢ╝ĒĢĀ ņäĖĻ░Ćņ¦Ć ļ¼ĖņĀ£ņŚÉ ļīĆĒĢ┤ ĒåĀņØśĒĢśņśĆļŗż. (1) ņŻ╝ņ¢┤ņ¦ä ĻĄ¼ņĪ░ņØś Ēśäņ×¼ ņāüĒā£ņØś ņŚÉļäłņ¦ĆņÖĆ ĒלņØä ņśłņĖĪĒĢśļŖö Structure to Energy and Force (S2EF), (2) ņŻ╝ņ¢┤ņ¦ä ĻĄ¼ņĪ░ļĪ£ļČĆĒä░ ĒĢ┤ļŗ╣ ĻĄ¼ņĪ░Ļ░Ć Ļ░Ćņ¦ł ņłś ņ׳ļŖö Ļ░Ćņן ņĢłņĀĢĒĢ£ ņāüĒā£ņØś ĻĄ¼ņĪ░ļź╝ ņśłņĖĪĒĢśļŖö Initial Structure to Relaxed Structure (IS2RS), (3) ņŻ╝ņ¢┤ņ¦ä ĻĄ¼ņĪ░ļĪ£ļČĆĒä░ ĒĢ┤ļŗ╣ ĻĄ¼ņĪ░Ļ░Ć Ļ░Ćņ¦ł ņłś ņ׳ļŖö Ļ░Ćņן ņĢłņĀĢĒĢ£ ņāüĒā£ņØś ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśļŖö Initial Structure to Relaxed Energy (IS2RE)ņØ┤ļ®░ OC20 ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżĻ░Ć ņĀ£Ļ│ĄļÉ£ Ēøä ņØ┤ļź╝ ĒÖ£ņÜ®ĒĢśņŚ¼ ņŻ╝ņ¢┤ņ¦ä ņäĖ Ļ│╝ņĀ£ļź╝ ĒĢ┤Ļ▓░ĒĢśļŖö ņŚ░ĻĄ¼ļōżņØ┤ ĻŠĖņżĆĒ׳ ļ│┤Ļ│ĀļÉśĻ│Ā ņ׳ļŗż[30ŌĆō32].
ņØ┤ļ¤¼ĒĢ£ ļ░®ļīĆĒĢ£ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļŖö ĻĖ░Ļ│äĒĢÖņŖĄņØä ņ£äĒĢ£ ĒĢÖņŖĄļŹ░ņØ┤Ēä░ļź╝ ņĀ£Ļ│ĄĒĢĀ ļ┐Éļ¦ī ņĢäļŗłļØ╝ ņøÉņåīņ╣śĒÖśļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ ĒÖöĒĢÖ Ļ│ĄĻ░ä ĒÖĢņןņŚÉ ņé¼ņÜ®ļÉśņ¢┤ ļśÉ ļŗżļźĖ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżņÖĆ ļ¬©ļŹĖ Ļ░£ļ░£ņŚÉ Ēü░ ļÅäņøĆņØä ņżä ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤ Wang et al. (2021)[33]ņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö MP ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļĪ£ļČĆĒä░ 9,524 Ļ░£ņØś Ļ▓░ņĀĢĻĄ¼ņĪ░ļź╝ ņČöņČ£ĒĢ£ Ēøä, [Fig 8]Ļ│╝ Ļ░ÖņØ┤ ĒÖöĒĢÖņĀü ņä▒ņ¦łņØ┤ ļ╣äņŖĘĒĢ£ ņøÉņåīļĪ£ ņ╣śĒÖśĒĢśļ®┤ņä£ ņŚ┤ņŚŁĒĢÖņĀüņ£╝ļĪ£ ņĢłņĀĢĒĢ£ ļ¼╝ņ¦łņØä ņ░ŠļŖö Ļ│╝ņĀĢņØä Ļ▒░ņ│É 189,981Ļ░£ņØś Ļ▓░ņĀĢ ĻĄ¼ņĪ░ ļŹ░ņØ┤Ēä░ļź╝ ņāØņä▒ĒĢśĻ│Ā 18,479Ļ░£ņØś ņĢłņĀĢĒĢ£ ļ¼╝ņ¦łņØä ļ░£Ļ▓¼ĒĢśņśĆĻ│Ā, ĒĢ┤ļŗ╣ ņøÉņåīņ╣śĒÖśļ▓ĢņØ┤ ņ×äņØś ĻĄ¼ņĪ░ļź╝ Ļ│äņé░ĒĢśņŚ¼ ĻĄ¼ņĪ░ļŹ░ņØ┤Ēä░ļź╝ ņłśņ¦æĒĢśĻ│Ā ņøÉĒĢśļŖö ĒŖ╣ņä▒ņØä Ļ░Ćņ¦ĆļŖö ļ¼╝ņ¦łņØä ņ░ŠļŖö ļ░®ļ▓Ģļ│┤ļŗż ļŹö ĒÜ©ņ£©ņĀüņ×äņØä ĒÖĢņØĖĒĢśņśĆļŗż. ĒĢ┤ļŗ╣ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżļŖö ņĄ£ņĀüĒÖö ņĀä ĻĄ¼ņĪ░ļź╝ ņĀ£Ļ│ĄĒĢśĻ│Ā ņ׳ĻĖ░ņŚÉ ņĢ×ņä£ ņ¢ĖĻĖēļÉ£ ņäĖ Ļ│╝ņĀ£ ņżæ IS2RS Ēś╣ņØĆ IS2REļź╝ ņłśĒ¢ēĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņé¼ņÜ®ļÉĀ ņłś ņ׳ļŗż[34].
3.2 ĻĖ░Ļ│äĒĢÖņŖĄņØä ņ£äĒĢ£ ņøÉņ×É ĻĄ¼ņĪ░ņØś ņ×ģļĀź ĒŖ╣ņä▒ ļ│ĆĒÖś
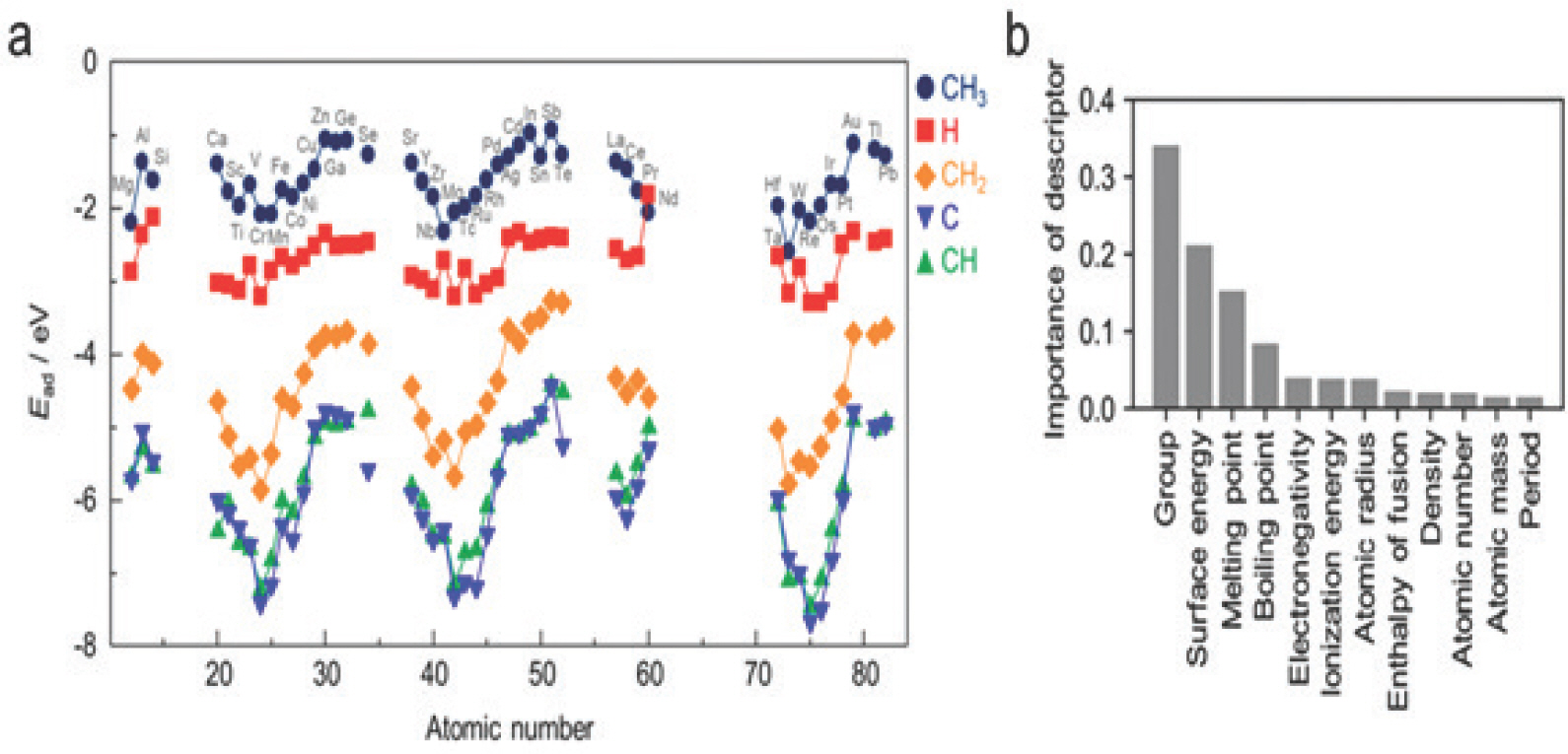
ņĀüņĀłĒĢ£ ņ×ģļĀź ĒŖ╣ņä▒ņØś ņäĀĒāØņØĆ ĻĖ░Ļ│äĒĢÖņŖĄ ļ¬©ļŹĖņØś ņä▒ļŖźņŚÉ ņ¦üņĀæņĀüņ£╝ļĪ£ ņśüĒ¢źņØä ļü╝ņ╣śļ®░ ņ×ģļĀź ĒŖ╣ņä▒Ļ│╝ ļ¬®Ēæ£Ļ░Æ Ļ░äņØś ļ¼╝ļ”¼ņĀüņØĖ Ļ┤ĆĻ│äļź╝ ĒīīņĢģĒĢśļŖö ļŹ░ ļÅäņøĆņØä ņżĆļŗż[35]. ļö░ļØ╝ņä£ ņ×ģļĀź ĒŖ╣ņä▒ņØä ņāØņä▒ĒĢĀ ļĢī ņČöĻ░ĆņĀüņØĖ Ļ│äņé░ ļ╣äņÜ®ņØ┤ ņĀüĻ│Ā ņ¦üĻ┤ĆņĀüņØĖ Ēæ£ĒśäņØ┤ Ļ░ĆļŖźĒĢ£ ņ×ģļĀź ĒŖ╣ņä▒ņØä ņäĀĒāØĒĢ┤ņĢ╝ ĒĢ£ļŗż[36]. ņ┤ēļ¦żļź╝ Ēæ£ĒśäĒĢśļŖö Ļ░Ćņן ļŗ©ņł£ĒĢ£ ņ×ģļĀź ĒŖ╣ņä▒ņØĆ ĒĢ┤ļŗ╣ ļ¼╝ņ¦łņØä ņØ┤ļŻ©ļŖö ņøÉņåīņØś ļ╣äņ£©ņØä ļ▓ĪĒä░ļĪ£ Ēæ£ĒśäĒĢśļŖö Ļ▓āņØ┤ļŗż. ņśłļź╝ ļōżņ¢┤ [Fig 9]ņÖĆ Ļ░ÖņØ┤ ņøÉņåīņØś ļ╣äņ£©ņØä One-hot-encoding ĻĖ░ļ▓Ģ[37]ņØä ĒåĄĒĢ┤ ĻĖ░Ļ│äĒĢÖņŖĄ ļ¬©ļŹĖņØ┤ ņØĮņØä ņłś ņ׳ļŖö ĒśĢĒā£ļĪ£ ļ│ĆĒÖśĒĢĀ ņłś ņ׳ļŗż. ņĀĢļ¤ēņĀüņ£╝ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŖö ļŗżņ¢æĒĢ£ ņøÉņåīņØś ĻĖ░ļ│Ė ĒŖ╣ņä▒ Ļ░Æ (ņøÉņ×É ļ░śņ¦Ćļ”ä, ņĀäĻĖ░ ņØīņä▒ļÅä ļō▒)ņØä ņØ┤ņÜ®ĒĢśļŖö Ļ▓āļÅä ņ┤ēļ¦żļź╝ ļ▓ĪĒä░ļĪ£ Ēæ£ĒśäĒĢśļŖö ĒÜ©Ļ│╝ņĀüņØĖ ļ░®ļ▓ĢņØ┤ļŗż[38].ņśłļź╝ ļōżņ¢┤, Toyao et al. (2018)[38]ņØĆ 12Ļ░Ćņ¦ĆņØś ņøÉņåī ĒŖ╣ņä▒ (ņØ┤ņś©ĒÖö ņŚÉļäłņ¦Ć, ņĪ▒, ņĀäĻĖ░ ņØīņä▒ļÅä, ņ£ĄĒĢ┤ņŚ┤, Ēæ£ļ®┤ ņŚÉļäłņ¦Ć, ļģ╣ļŖö ņĀÉ, ļüōļŖö ņĀÉ, ņøÉņ×É ļ░śņ¦Ćļ”ä, ļ░ĆļÅä, ņŻ╝ĻĖ░, ņøÉņ×É ļ▓łĒśĖ, ņøÉņ×É ņ¦łļ¤ē)ņ£╝ļĪ£ ĻĄ¼ļ”¼ ĻĖ░ļ░ś ĒĢ®ĻĖł ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ņØś CH3, CH2, CH, C ĻĘĖļ”¼Ļ│Ā HņØś ĒØĪņ░® ņŚÉļäłņ¦Ćļź╝ Ordinary Linear Regression (ORE), Random Forest Regressor (RFR), Gradient Boosting Regressor (GBR) ĻĘĖļ”¼Ļ│Ā Extra Tree Regressor (ETR) ļō▒ņØś ĻĖ░Ļ│äĒĢÖņŖĄ ļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢśņŚ¼ Root Mean Square Error (RMSE) 0.3 eV ņØ┤ĒĢśņØś ņĀĢĒÖĢļÅäļĪ£ ņśłņĖĪĒĢśļŖö ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ļśÉĒĢ£, ņ×ģļĀź ĒŖ╣ņä▒ņØś ņØĖņ×ÉļĪ£ ņé¼ņÜ®ĒĢ£ ņøÉņåī ĒŖ╣ņä▒Ļ│╝ ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś Ļ┤ĆĻ│äļź╝ ļČäņäØĒĢśņŚ¼ [Fig 10a]ņÖĆ Ļ░ÖņØ┤ ņøÉņåīņØś ņĪ▒ņŚÉ ļö░ļźĖ ĒØĪņ░®ņŚÉļäłņ¦Ć ļ│ĆĒÖöņØś Ļ▓ĮĒ¢źņØä ĒÖĢņØĖĒĢśņśĆĻ│Ā, ETR ņśłņĖĪ Ļ▓░Ļ│╝ļĪ£ļČĆĒä░ ņ¢╗ņØä ņłś ņ׳ļŖö ĒŖ╣ņä▒ ņżæņÜöļÅä (Feature Importance) ņĀÉņłśļĪ£ļČĆĒä░ ņĪ▒ņØ┤ CH3 ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśļŖö ļŹ░ Ļ░Ćņן ņżæņÜöĒĢ£ ņĀĢļ│┤ņ×äņØä ņĢī ņłś ņ׳ņŚłļŗż [Fig 10b]. ņČöĻ░ĆņĀüņ£╝ļĪ£ Ēæ£ļ®┤ņŚÉļäłņ¦Ć, ļģ╣ļŖöņĀÉ, ļüōļŖöņĀÉ ļō▒ņØ┤ ņżæņÜöĒĢ£ ņØĖņ×Éņ×äņØä ĒÖĢņØĖĒĢśņśĆļŗż. ņØ┤ņ▓śļ¤╝ ņ×ģļĀź ĒŖ╣ņä▒ņØś ņØĖņ×ÉļĪ£ ņĀüņĀłĒĢ£ ņøÉņåī ĒŖ╣ņä▒ņØä ņäĀĒāØĒĢśļ®┤ ņĀüņØĆ ļ╣äņÜ®ņ£╝ļĪ£ ļ│Ąņ×ĪĒĢ£ ņ┤ēļ¦ż ĒŖ╣ņä▒ņØä ņśłņĖĪĒĢĀ ņłś ņ׳Ļ│Ā ņØĖņ×ÉņÖĆ ĒŖ╣ņä▒ Ļ░äņØś ņāüĻ┤Ć Ļ┤ĆĻ│äļÅä ĒĢÖņŖĄĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā9.
ņøÉņåī ļ╣äņ£©ņØä Ēæ£ĒśäĒĢśĻĖ░ ņ£äĒĢ£ One-hot Encoding ĻĖ░ļ▓Ģ. Adapted from Perterson et al. JPhys energy

Fig.┬Ā10.
a) ņøÉņ×É ļ▓łĒśĖņŚÉ ļö░ļźĖ ĒØĪņ░®ļ¼╝ņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ļ│ĆĒÖö, b) ņøÉņåī ĒŖ╣ņä▒ņ£╝ļĪ£ ĒĢÖņŖĄĒĢ£ Extra Tree Regressor ļ¬©ļŹĖņØś CH3 ĒØĪņ░®ņŚÉļäłņ¦Ć ņśłņĖĪ Ļ▓░Ļ│╝ņŚÉ ļīĆĒĢ£ ĒŖ╣ņä▒ ņżæņÜöļÅä (Feature importance) ņĀÉņłś. ņĀÉņłśĻ░Ć ļåÆņØäņłśļĪØ ĒĢ┤ļŗ╣ ĒŖ╣ņä▒ņØ┤ ņśłņĖĪņŚÉ ņżæņÜöĒĢ£ ņØĖņ×Éņ×äņØä ņØśļ»Ė. Adapted with permission from Toyao et al. J. Phys. Chem. C 2018;122;8315 Copyright 2018 American Chemical Society.
ņĀäņ×ÉĻĄ¼ņĪ░ņĀü ņĀĢļ│┤ ņŚŁņŗ£ ņ×ģļĀź ĒŖ╣ņä▒ņØś ņØĖņ×ÉļĪ£ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ļŗż[39]. ņĀäņ×ÉĻĄ¼ņĪ░ņĀü ņĀĢļ│┤ļŖö ņ¢╗ĻĖ░ ņ£äĒĢ┤ ņĀ£ņØ╝ņøÉļ”¼Ļ│äņé░ņØ┤ ĒĢäņÜöĒĢ©ņŚÉļÅä ņĀäĻĖ░ĒÖöĒĢÖņĀü ņ┤ēļ¦ż ĒŖ╣ņä▒ ņśłņĖĪņŚÉ Ēü░ ņŚŁĒĢĀņØä ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ĻĖ░Ļ│äĒĢÖņŖĄņØś ņ×ģļĀź Ēæ£Ēśä ņØĖņ×ÉļĪ£ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ļŗż[40]. ĻĖłņåŹņØś d-band centerņØś Ļ▓ĮņÜ░ ļŗżņ¢æĒĢ£ ļ░śņØæņŚÉ ļīĆĒĢ£ ĒÖ£ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉĻ░Ć[41ŌĆō43] ļÉśļ®░ d-band centerļź╝ ļ│┤ņÖäĒĢ£ e g ņśżļ╣äĒāłņØś filling[44, 45]Ļ│╝ d-band upper edge[46] ņŚŁņŗ£ ņĀäņ×É ĻĄ¼ņĪ░ ĒŖ╣ņä▒ Ļ▓░ņĀĢ ņØĖņ×ÉļĪ£ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ļŗż. Noh et al. (2018)[47]ņØĆ d-band ļ¬©ļ®śĒŖĖ ĒŖ╣ņä▒ņØä ņ¢╗ĻĖ░ ņ£äĒĢ£ Ļ│äņé░ņŚÉ ļō£ļŖö ļ╣äņÜ®ņØä ņĀłĻ░ÉĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņĀ£ņØ╝ņøÉļ”¼Ļ│äņé░ņØ┤ ĒĢäņÜöĒĢśņ¦Ć ņĢŖņØĆ Linear Muffin-Tin Orbital Theory (LMTO)ņŚÉ ĻĖ░ļ░śĒĢ£ d-band ļäōņØ┤ņÖĆ ĒÅēĻĘĀ ņĀäĻĖ░ņØīņä▒ļÅäļź╝ descriptor ļź╝ ņé¼ņÜ®ĒĢśņŚ¼ COŌłŚ ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ RMSE 0.05 eVņØś ņĀĢĒÖĢļÅäļĪ£ ņśłņĖĪĒĢśņśĆļŗż. ņĄ£ĻĘ╝ņŚÉļŖö DOSļź╝ Ļ░äņĀæņĀüņ£╝ļĪ£ ļéśĒāĆļé┤ļŖö ļ¬©ļ®śĒŖĖ ĒŖ╣ņä▒ ļīĆņŗĀ DOS ņĀäņ▓┤ļź╝ ņØĖņ×ÉļĪ£ ņé¼ņÜ®ĒĢśņŚ¼ ĒÖ£ņä▒ņØä ņśłņĖĪĒĢśļŖö ņŚ░ĻĄ¼ Ļ▓░Ļ│╝Ļ░Ć ļ│┤Ļ│ĀļÉśņŚłļŗż. Victor et al. (2021)[48]ņØĆ ņ┤ēļ¦ż Ēæ£ļ®┤ ĒØĪņ░® ņ×Éļ”¼ ņøÉņ×ÉļĪ£ļČĆĒä░ Ļ│äņé░ĒĢ£ ņØ╝ņĀĢ ņŚÉļäłņ¦Ć ļ▓öņ£äņØś DOSļź╝ ņ¦üņĀæņĀüņ£╝ļĪ£ ĒĢ®ņä▒Ļ│▒ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØś ņ×ģļĀź Ēæ£ĒśäĻ░Æņ£╝ļĪ£ ņé¼ņÜ®ĒĢśņŚ¼ ļŗżņ¢æĒĢ£ ĒØĪņ░®ļ¼╝ņØś ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśļŖö DOSnet ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż [Fig 11]. ĻĘĖ Ļ▓░Ļ│╝ ĒÅēĻĘĀņĀüņ£╝ļĪ£ Mean Absolute Error (MAE) 0.138 eVņØś ņĀĢĒÖĢļÅäļź╝ ļ│┤ņśĆĻ│Ā ņØ┤ļŖö ņĀĢļ¤ēņĀüņØĖ d-band ļ¬©ļ®śĒŖĖ ĒŖ╣ņä▒ņØä descriptorļĪ£ ņé¼ņÜ®ĒĢśļŖö ļ¬©ļŹĖĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ ļåÆņØĆ ņĀĢĒÖĢļÅäņśĆļŗż. ņØ┤ņŚÉ ļŹöĒĢ┤ ĒØĪņ░®ļ¼╝ņØś DOSļź╝ ĒżĒĢ©ĒĢ£ ņĀäņØ┤ ĒĢÖņŖĄ (transfer learning)ņØä ĒåĄĒĢ┤ MAEļź╝ 0.116 eVĻ╣īņ¦Ć ļé«ņČ£ ņłś ņ׳ņ£╝ļ®░ ņĄ£ņĀüĒÖöļÉśņ¦Ć ņĢŖņØĆ Ēæ£ļ®┤ņØś DOSļź╝ ņ×ģļĀźĻ░Æņ£╝ļĪ£ ņé¼ņÜ®ĒĢśļŹöļØ╝ļÅä MAE 0.128 eVņØś ņČ®ļČäĒ׳ ļåÆņØĆ ņĀĢĒÖĢļÅäļź╝ ļ│┤ņŚ¼ DOSnetņØĆ ņĀ£ņØ╝ņøÉļ”¼Ļ│äņé░ ņŚåņØ┤ļÅä ņé¼ņÜ® Ļ░ĆļŖźĒĢśļŗżļŖö Ļ▓āņØä ļ│┤ņśĆļŗż. ņØ┤ ņÖĖņŚÉļÅä Esterhuizen et al. (2021)[49]ņØĆ Principal Component Analysis (PCA)ļź╝ ņé¼ņÜ®ĒĢśņŚ¼ DOSļź╝ ņ░©ņøÉ ņČĢņåīņŗ£Ēé© ļ╣äņ¦ĆļÅä ĒĢÖņŖĄņØä ĒåĄĒĢ┤ ĒĢ®ĻĖł ņ┤ēļ¦żņØś ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢ£ Ļ▓░Ļ│╝, ļ¬©ļ®śĒŖĖ ĒŖ╣ņä▒ņØä ņé¼ņÜ®ĒĢ£ ļ¬©ļŹĖļ│┤ļŗż ļåÆņØĆ ņĀĢĒÖĢļÅäļź╝ ļŗ¼ņä▒ĒĢśņśĆļŗż.
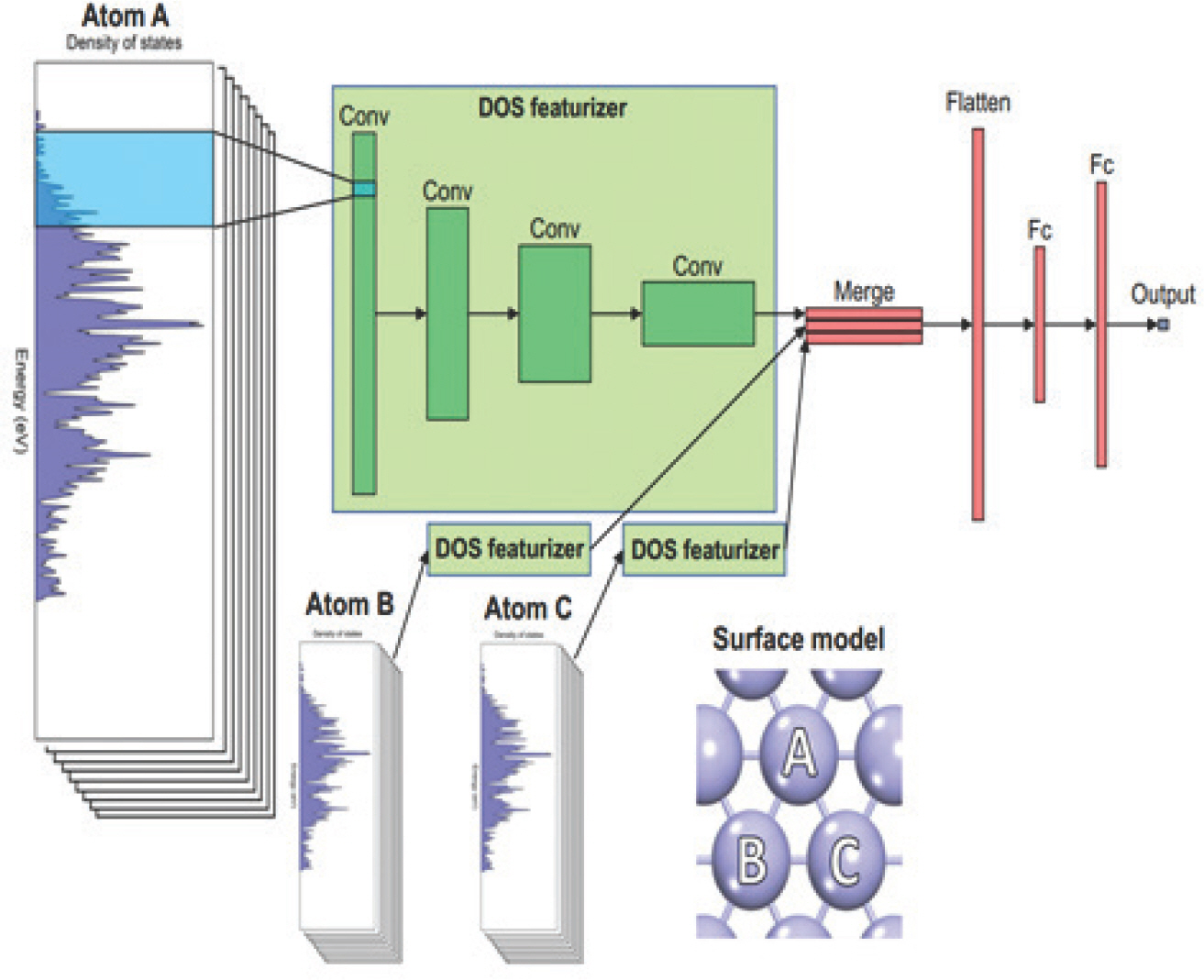
Fig.┬Ā11.
DOSnetņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ņśłņĖĪ Ļ│╝ņĀĢ. Ēæ£ļ®┤ ĒÖ£ņä▒ ņ×Éļ”¼ ņøÉņ×ÉņØś DOSļź╝ ņ×ģļĀź Ēæ£Ēśäļ▓Ģņ£╝ļĪ£ ĒĢ®ņä▒Ļ│▒ ņØĖĻ│ĄņŗĀĻ▓Įļ¦Ø (Convolutional Neural Network) (ņ┤łļĪØ) Ļ│╝ ņÖäņĀä ņŚ░Ļ▓░ ļ¦Ø (Fully Connected Layer) (ļ╣©Ļ░Ģ)ņØä ņ¦Ćļéś ņČ£ļĀźĻ░Æ (Output)ņØĖ ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢ£ļŗż. ĒÖ£ņä▒ ņ×Éļ”¼ ņøÉņ×ÉĻ░Ć 2Ļ░£ ņØ┤ņāüņØ╝ Ļ▓ĮņÜ░ Ļ░üĻ░üņØś ĒĢ®ņä▒Ļ│▒ Ļ│äņĖĄ Ļ▓░Ļ│╝ļź╝ ļ│æĒĢ®ĒĢ£ļŗż. Adapted from Fung et al. Nat. Commun. 2021;12;1.
ņ┤ēļ¦żņØś ĻĄ¼ņĪ░ņĀüņØĖ ņĀĢļ│┤ļź╝ ļ░śņśüĒĢśļŖö ņØĖņ×ÉļÅä ĒØĪņ░® ĒŖ╣ņä▒ ņśłņĖĪņŚÉ ņ£ĀņÜ®ĒĢśĻ▓ī ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż. ĻĄ¼ņĪ░ ņĀĢļ│┤ļŖö ņøÉņ×ÉĻ░ä Ļ▒░ļ”¼, Ļ░üļÅäņÖĆ Space Group, Wyckoff Positionļō▒ņØ┤ ņ׳ņ£╝ļ®░, ņ┤ēļ¦ż Ēæ£ļ®┤ņŚÉņä£ ļ░śņØæņżæĻ░äņ▓┤Ļ░Ć ĒØĪņ░®ĒĢśļŖö ĒÖ£ņä▒ ņ×Éļ”¼ņØś ļ░░ņ£äņłś (coordination number (CN))[50ŌĆō52]ļÅä ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĻĄ¼ņĪ░ ņĀĢļ│┤ļŖö ņøÉņåī ņĀĢļ│┤, ņĀäņ×É ĻĄ¼ņĪ░ ĒŖ╣ņä▒Ļ│╝ ļÅÖņŗ£ņŚÉ ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż. ņśłļź╝ ļōżņ¢┤ Batchelor et al. (2019)[53]ņØĆ High Entropy Alloy (HEA) ņ┤ēļ¦ż Ēæ£ļ®┤ņØś ĒÖ£ņä▒ņ×Éļ”¼ņÖĆ ĒÖ£ņä▒ņ×Éļ”¼ ņøÉņåīņØś ņĄ£ĻĘ╝ļ”░ ņøÉņ×É, ņĢäļלņĖĄņØś ņĄ£ĻĘ╝ļ”░ ņøÉņ×Éļź╝ ĻĄ¼ļČäĒĢśņŚ¼ ĒĢÖņŖĄņŗ£ņ╝£ OŌłŚņÖĆ OHŌłŚņØś ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ Root Mean Square Deviation (RMSD) 0.06~0.07 eVņØś ņĀĢĒÖĢļÅäļĪ£ ņśłņĖĪĒĢśņśĆļŗż. TranĻ│╝ UlissiņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö Voronoi tessellation ĻĖ░ļ▓Ģņ£╝ļĪ£ Ļ▓░ņĀĢļÉ£ ĒØĪņ░®ļ¼╝ņØś ļ░░ņ£äņłśņÖĆ ņøÉņ×É ļ▓łĒśĖ, Pauling ņĀäĻĖ░ņØīņä▒ļÅäļź╝ ņ×ģļĀź Ēæ£Ēśä ņØĖņ×ÉļĪ£ ņé¼ņÜ®ĒĢśņŚ¼ ĒĢ®ĻĖł ņ┤ēļ¦żņØś COŌłŚ, HŌłŚ ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśņśĆĻ│Ā, ņØ┤ņé░ĒÖöĒāäņåī ĒÖśņøÉ ļ░śņØæĻ│╝ ņłśņåī ļ░£ņāØ ļ░śņØæņŚÉ ņ£Āļ¦ØĒĢ£ ĒĢ®ĻĖł ņ┤ēļ¦ż Ēæ£ļ®┤ņØä Ļ░üĻ░ü 131Ļ░£, 258Ļ░£ļź╝ ļ░£Ļ▓¼ĒĢśņŚ¼ ļ│┤Ļ│ĀļÉśņ¦Ć ņĢŖņØĆ ņŗĀĻĘ£ ņ┤ēļ¦żļź╝ ņĀ£ņŗ£ĒĢ£ ļ░ö ņ׳ļŗż.
ņĄ£ĻĘ╝ņŚÉļŖö ĻĄ¼ņĪ░ ņĀĢļ│┤ļź╝ ņŚ¼ļ¤¼ Ļ░£ņØś ņĀĢļ¤ēņĀüņØĖ ņØĖņ×ÉļĪ£ ļéśĒāĆļé┤ļŖö ļ¬©ļŹĖ ļ┐Éļ¦ī ņĢäļŗłļØ╝, ņøÉņ×ÉņØś ņóīĒæ£ ņĀĢļ│┤ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ēæ£ļ®┤ Ēś╣ņØĆ Ļ▓░ņĀĢ ĻĄ¼ņĪ░ļź╝ ĻĘĖļלĒöäļĪ£ ļéśĒāĆļé┤ļŖö ņŚ░ĻĄ¼Ļ░Ć Ļ░üĻ┤æņØä ļ░øĻ│Āņ׳ļŗż. XieņÖĆ Grossman (2018)[54]ņØĆ Ļ▓░ņĀĢ ĻĘĖļלĒöäļź╝ ņ×ģļĀź Ēæ£Ēśäļ▓Ģņ£╝ļĪ£ ņé¼ņÜ®ĒĢśĻ│Ā ĒĢ®ņä▒Ļ│▒ ņØĖĻ│ĄņŗĀĻ▓Įļ¦Ø (CNN)ņØä ņĀüņÜ®ĒĢśņŚ¼ CGCNN ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆĻ│Ā, Back et al. (2019)[55]ņØĆ Voronoi tessellationņØä ņØ┤ņÜ®ĒĢ┤ ĒØĪņ░®ļ¼╝ņØś ņĄ£ĻĘ╝ļ”░ Ēæ£ļ®┤ ņøÉņ×Éļź╝ ĒāÉņāēĒĢśĻ│Ā ņØ┤ļź╝ ņØ┤ņÜ®ĒĢ£ ņāłļĪ£ņÜ┤ ĒÖ£ņä▒ņ×Éļ”¼ Ēæ£Ēśäļ▓ĢņØä Ļ░£ļ░£ĒĢśņśĆļŗż [Fig 12]. ņØ┤ ļ¬©ļŹĖņØĆ COŌłŚņÖĆ HŌłŚ ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ MAE 0.15 eVņØś ņĀĢĒÖĢļÅäļĪ£ ļ¦żņÜ░ ņĀĢĒÖĢĒĢśĻ▓ī ņśłņĖĪĒĢśņśĆĻ│Ā, ĒÖ£ņä▒ņ×Éļ”¼ņØś ņ▓½ļ▓łņ¦Ė, ļæÉļ▓łņ¦Ė ņĄ£ĻĘ╝ļ”░ ņøÉņ×ÉĻ░Ć ĒØĪņ░®ņŚÉļäłņ¦Ć Ļ▓░ņĀĢņŚÉ Ēü░ ņśüĒ¢źņØä ņŻ╝ļŖö Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż.
Fig.┬Ā12.
nĻ░£ņØś ņøÉņ×Éļź╝ ĒżĒĢ©ĒĢśļŖö ņ┤ēļ¦ż Ēæ£ļ®┤ ĻĄ¼ņĪ░ļź╝ CNNņØś ņ×ģļĀź Ēæ£ĒśäņØä ņ£äĒĢ£ ĻĘĖļלĒöäļĪ£ ļ│ĆĒÖśĒĢśļŖö Ļ│╝ņĀĢ. a) One-hot Encoding ļÉ£ 9Ļ░£ņØś ĻĖ░ņ┤łņĀüņØĖ ņøÉņåī ĒŖ╣ņä▒ņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ņøÉņ×É ĒŖ╣ņä▒ ļ▓ĪĒä░, b) Voronoi polyhedronņ£╝ļĪ£ ļČĆĒä░ ņ¢╗ņØĆ solid angle (╬®)ļĪ£ ņøÉņ×ÉņØś ņØ┤ņøā ņĀĢļ│┤ļź╝ ņāØņä▒, c) Ēæ£ļ®┤ ņøÉņ×ÉņÖĆ ĒØĪņ░®ļ¼╝ Ļ░äņØś ņŚ░Ļ▓░ Ļ▒░ļ”¼ ņĖĪņĀĢ. Adapted with permission from Back et al. J. Phys. Chem. 2019;10;4401 Copyright 2019 American Chemical Society.

ņØ┤ ņÖĖņŚÉļÅä ņ┤ēļ¦ż ĻĄ¼ņĪ░ļź╝ ĻĘĖļלĒöäļĪ£ ļ│ĆĒÖśĒĢśņŚ¼ ņ×ģļĀź Ēæ£Ēśäļ▓Ģņ£╝ļĪ£ ņé¼ņÜ®ĒĢśļŖö ļ¬©ļŹĖņØĆ ņøÉņ×ÉĻ░ä Ļ▓░ĒĢ® ĒśĢĒā£, ĒÅēĻĘĀ ņøÉņ×É Ļ▓░ĒĢ® ņłśņÖĆ Ļ░ÖņØĆ Ļ▓░ĒĢ® ļ░Å ĻĄŁņåī ņĀĢļ│┤ļź╝ ĒżĒĢ©ĒĢśņŚ¼ Ļ▓░ņĀĢ ĻĄ¼ņĪ░ ĒŖ╣ņä▒ņØä ņśłņĖĪĒĢśļŖö MEGNet (2019)[56], ĒÖ£ņä▒ņ×Éļ”¼ ņĀĢļ│┤ļź╝ ĻĘĖļלĒöäņŚÉ ļØ╝ļ▓©ļ¦üĒĢśļŖö LS-CGCNN (2020)[57], ļ▓īĒü¼ņÖĆ Ēæ£ļ®┤ ĻĄ¼ņĪ░ļź╝ ļö░ļĪ£ ĻĘĖļלĒöäļĪ£ ļ│ĆĒÖśĒĢśņŚ¼ ĒĢ®ņ╣śļŖö SGCNN (2019) ļō▒ ļŗżņ¢æĒĢ£ ļ░®ņŗØņ£╝ļĪ£ Ļ░£ļ░£ļÉśņ¢┤ ĻĘĖļלĒöä Ēæ£Ēśäļ▓ĢņØ┤ ĒÖ£ņä▒, ņĢłņĀĢņä▒ ļō▒ ņ┤ēļ¦ż ĒŖ╣ņä▒ņØä ņśłņĖĪĒĢśĻĖ░ņŚÉ ņóŗņØĆ ņ×ģļĀź Ēæ£Ēśäļ▓ĢņØ┤ļØ╝ļŖö Ļ▓āņØä ļ│┤ņŚ¼ņŻ╝ņŚłļŗż [Fig 13]. ļśÉĒĢ£ ņøÉņ×ÉĻ░ä Ļ▒░ļ”¼ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņĀ£ņ×æĒĢ£ Ļ▓░ņĀĢ ĻĘĖļלĒöäļź╝ ņé¼ņÜ®ĒĢśĻĖ░ ņ£äĒĢ┤ DFT ĻĄ¼ņĪ░ ņĄ£ņĀüĒÖöĻ░Ć ļÅÖļ░śļÉśņ¢┤ņĢ╝ ĒĢ£ļŗżļŖö ĒĢ£Ļ│äļź╝ ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢ┤ ņøÉņ×ÉņØś ļ░®Ē¢ź ņĀĢļ│┤[31]ļéś Wyckoff Position[34] ļō▒ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ▓░ņĀĢ ĻĘĖļלĒöäļź╝ ņĀ£ņ×æĒĢśĻ│Ā ņĢłņĀĢņä▒ ļō▒ņØś ĒŖ╣ņä▒ņØä ņśłņĖĪĒĢśļŖö ņŚ░ĻĄ¼ļÅä ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż. ĒŖ╣Ē׳ ņøÉņ×ÉņØś Wyckoff PositionņØä ņ×ģļĀź Ēæ£ĒśäĻ░Æņ£╝ļĪ£ ņØ┤ņÜ®ĒĢśņŚ¼ ņĄ£ņĀüĒÖöļÉśņ¦Ć ņĢŖņØĆ ĻĄ¼ņĪ░ņØś ĒśĢņä▒ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśļŖö ļ¬©ļŹĖņØ┤ ļ│┤Ļ│ĀļÉ£ ļ░ö ņ׳ļŗż.
Fig.┬Ā13.
a) Materials Graph Network (MEGNet)ņØś ļ¼╝ņ¦ł Ēæ£Ēśä Ļ│╝ņĀĢ. Adapted with permission from Chen et al. Chem. Mater. 2019;31.9;3564-72 Copyright 2019 American Chemical Society. b) Labeled-Site CGCNN (LS-CGCNN)ņØś ĒØĪņ░®ņŚÉļäłņ¦Ć ņśłņĖĪ ļ░®ļ▓Ģ. Ēæ£ļ®┤ ĻĘĖļלĒöäņØś ĒÖ£ņä▒ņ×Éļ”¼ļź╝ ļØ╝ļ▓©ļ¦üĒĢśņŚ¼ ļ¬©ļŹĖņØä ĒĢÖņŖĄĒĢ£ļŗż. Adapted with permission from Gu et al. J. Phys. Chem. 2020;11.9;3185-91 Copyright 2020 American Chemical Society. c) Slab Graph Convolutional Neural Network (SGCNN)ņØś Ēæ£ļ®┤ ĻĘĖļלĒöä ļ│ĆĒÖś Ļ│╝ņĀĢ. Ēæ£ļ®┤Ļ│╝ ļ▓īĒü¼ ĻĄ¼ņĪ░ļź╝ Ļ░üĻ░ü ĻĘĖļלĒöäļĪ£ ļ│ĆĒÖśņŗ£ĒéżĻ│Ā ņØ┤ļōżņØä ņŚ«ņ¢┤ ļ¬©ļŹĖņØä ĒĢÖņŖĄĒĢ£ļŗż. Adapted with permission from Kim et al. Chem. Mater. 2020;32;709-20 Copyright 2020 American Chemical Society.

ņøÉņ×É ĻĄ¼ņĪ░ņØś ņ×ģļĀź Ēæ£Ēśäļ▓Ģ ļ┐Éļ¦ī ņĢäļŗłļØ╝ ĻĖ░Ļ│äĒĢÖņŖĄ ņĢīĻ│Āļ”¼ņ”śņØś ņäĀĒāØ ņŚŁņŗ£ ņżæņÜöĒĢśļŗż. ņĀüņĀłĒĢ£ ņĢīĻ│Āļ”¼ņ”śņØä ņäĀĒāØĒĢśļ®┤ ļŗ©ņł£Ē׳ ņśłņĖĪ ņĀĢĒÖĢļÅäļź╝ ļåÆņŚ¼ņżä ļ┐Éļ¦ī ņĢäļŗłļØ╝ ĻĖ░Ļ│äĒĢÖņŖĄņØś Ļ│╝ņĀĢĻ│╝ Ļ▓░Ļ│╝ļź╝ ĒĢ┤ņäØĒĢśņŚ¼ ņ┤ēļ¦ż ļ░śņØæņŚÉ ļīĆĒĢ£ ĒåĄņ░░ņØä ņ¢╗ņØä ņłś ņ׳ļÅäļĪØ ĒĢ£ļŗż. ņśłļź╝ ļōżņ¢┤ Andersen et al. (2019)[58]ņØĆ Sure Independence Screening and Sparsifying Operator (SISSO) ņĢīĻ│Āļ”¼ņ”ś[59]ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĒĢ®ĻĖł Ēæ£ļ®┤ņØś ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ RMSE 0.2 eVņØś ņĀĢĒÖĢļÅäļĪ£ ņśłņĖĪĒĢśņśĆļŗż. SISSO ņĢīĻ│Āļ”¼ņ”śņØĆ [Fig 14]ņÖĆ Ļ░ÖņØ┤ ĒĢÖņŖĄ ļŹ░ņØ┤Ēä░ļĪ£ļČĆĒä░ ņ×ģļĀźĻ░ÆĻ│╝ ļ¬®Ēæ£Ļ░ÆņØś Ļ┤ĆĻ│äļź╝ ļ╣äņäĀĒśĢņŗØņ£╝ļĪ£ ļéśĒāĆļé╝ ņłś ņ׳ļŗż. ĒĢ┤ļŗ╣ ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ×ģļĀźĻ░Æņ£╝ļĪ£ ņ┤Ø 18Ļ░£ņØś ņøÉņåī, ļ▓īĒü¼, Ēæ£ļ®┤Ļ│╝ ņĀäņ×É ĻĄ¼ņĪ░ ĒŖ╣ņä▒ņØä ņé¼ņÜ®ĒĢśņśĆņ£╝ļ®░ SISSOļź╝ ĒåĄĒĢ┤ Ļ░üĻ░üņØś ĒĢ®ĻĖłļ¦łļŗż ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśņśĆļŗż. SISSO ņĢīĻ│Āļ”¼ņ”śņØĆ ņśłņĖĪ Ļ▓░Ļ│╝ ļÅäņČ£ Ļ│╝ņĀĢņØä ņé¼ļ×īņØ┤ ņØ┤ĒĢ┤ĒĢśĻĖ░ ĒלļōĀ ĒāĆ ņĢīĻ│Āļ”¼ņ”śņØ┤ļéś ņØĖĻ│Ą ņŗĀĻ▓Įļ¦ØĻ│╝ ļŗ¼ļ”¼ ņäĀĒśĢ ĒÜīĻĘĆņÖĆ Ļ░ÖņØ┤ Ļ░ü ņ×ģļĀź ĒŖ╣ņä▒ņØ┤ ņśłņĖĪņŚÉ ņ¢┤ļŖÉ ņĀĢļÅä ĻĖ░ņŚ¼ĒĢśņśĆļŖöņ¦Ć ņĀ£ņŗ£ĒĢĀ ņłś ņ׳ņ£╝ļ®░ ļåÆņØĆ ņĀĢĒÖĢļÅäļź╝ Ļ░Ćņ¦äļŗżļŖö ņןņĀÉņØ┤ ņ׳ļŗż. ĒĢ┤ļŗ╣ ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņØ┤ļź╝ ĒåĄĒĢ┤ Ļ░ü ĒØĪņ░®ņŚÉļäłņ¦Ć ņśłņĖĪņŚÉ ņĀüĒĢ®ĒĢ£ ĒŖ╣ņä▒ļōżņØä ĻĄ¼ļČäĒĢĀ ņłś ņ׳ņŚłļŗż.
Fig.┬Ā14.
SISSO ņĢīĻ│Āļ”¼ņ”śņØä ĒåĄĒĢ┤ ņĀ£ņ×æĒĢ£ IrRu ĒĢ®ĻĖł ĒŖ╣ņä▒Ļ│╝ C ŌłŚĒØĪņ░®ņŚÉļäłņ¦Ć Ļ░äņØś ļ╣äņäĀĒśĢņŗØ. Adapted with permission from Andersen et al. ACS Cat. 2019;9.4;2752-59 Copyright 2019 American Chemical Society.

ņØ┤ļĪĀņ£╝ļĪ£ļČĆĒä░ ļÅäņČ£ĒĢ£ Ļ┤ĆĻ│äņŗØņØä ĻĖ░Ļ│äĒĢÖņŖĄĻ│╝ Ļ▓░ĒĢ®ĒĢśņŚ¼ ņé¼ņÜ®ĒĢśļŖö ļ¬©ļŹĖļÅä ļ│┤Ļ│ĀļÉ£ ļ░ö ņ׳ļŗż. Wang et al. (2021)[60]ņØĆ ņśżļ╣äĒāł Ēś╝ņä▒ĒÖö (Orbital Hybridization)ņÖĆ ĒīīņÜĖļ”¼ ļ░śļ░£ (Pauli Repulsion)ņØä ņØ┤ņÜ®ĒĢ┤ ĒØĪņ░®ņŚÉļäłņ¦Ć Ēæ£Ēśäļ▓ĢņØä ĻĄ¼ņä▒ĒĢśĻ│Ā, ļ│Ćņłś Ļ░ÆņØä ņśłņĖĪĒĢśļŖö Ēæ£ļ®┤ ĻĘĖļלĒöä ĻĖ░ļ░ś ņØĖĻ│Ą ņŗĀĻ▓Įļ¦Ø ļ¬©ļŹĖĻ│╝ Ļ▓░ĒĢ®ĒĢśņŚ¼ Theory-infused Neural Network (TinNet) ņØä Ļ░£ļ░£ĒĢśņśĆļŗż [Fig 15]. ĒĢ┤ļŗ╣ ļ¬©ļŹĖņØĆ CGCNNĻ│╝ DOSnet ĻĘĖļ”¼Ļ│Ā ĻĄ¼ņĪ░ņĀü ĒŖ╣ņä▒Ļ│╝ ņĀäņ×É ĻĄ¼ņĪ░ ĒŖ╣ņä▒ņØä ņØ┤ņÜ®ĒĢśļŖö ĻĖ░ĒāĆ ņØĖĻ│Ą ņŗĀĻ▓Įļ¦Ø ļ¬©ļŹĖļ│┤ļŗż Ēø©ņö¼ Ē¢źņāüļÉ£ MAE 0.118 eVņØś ņĀĢĒÖĢļÅäļĪ£ ņĀäņØ┤ĻĖłņåŹ Ēæ£ļ®┤ņŚÉņä£ OH ĒØĪņ░®ņŚÉļäłņ¦Ćļź╝ ņśłņĖĪĒĢśņśĆļŗż. ņØ┤ņŚÉ ļŹöĒĢ┤ ĻĖłņåŹņØś ņśżļ╣äĒāłņŚÉ ļö░ļźĖ ņśłņĖĪļÉ£ ņØ┤ļĪĀ Ļ┤ĆĻ│äņŗØņØś ļ│Ćņłś Ļ░ÆĻ│╝ Ēś╝ņä▒ĒÖö ņŚÉļäłņ¦ĆĻ░äņØś ņäĀĒśĢ Ļ┤ĆĻ│äņŗØņØä ņĀ£Ļ│ĄĒĢśņŚ¼ ļ¬®Ēæ£Ļ░Æļ¦ī ņśłņĖĪĒĢśļŖö ĻĖ░ĒāĆ ņĢīĻ│Āļ”¼ņ”śĻ│╝ ļŗ¼ļ”¼ ĒÖ£ņä▒ņŚÉ ļīĆĒĢ£ ļ¼╝ļ”¼ņĀüņØĖ ĒĢ┤ņäØņØä ņĀ£Ļ│ĄĒĢĀ ņłś ņ׳ņŚłļŗż.
4. ĻĖ░Ļ│äĒĢÖņŖĄ ļ░®ļ▓ĢļĪĀņØś ĒĢ£Ļ│ä
Ļ│äņé░ĒÖöĒĢÖ ļČäņĢ╝ņŚÉņä£ ĻĖ░Ļ│äĒĢÖņŖĄņØĆ ņ┤ēļ¦ż ņä▒ļŖź ņśłņĖĪĻ│╝ ņāłļĪ£ņÜ┤ ņ┤ēļ¦ż ņäżĻ│äņŚÉ ņ׳ņ¢┤ ĒøīļźŁĒĢ£ ņä▒Ļ│╝ļź╝ ļ│┤ņŚ¼ņŻ╝ņŚłĻ│Ā, ņĢ×ņ£╝ļĪ£ ļŗżņ¢æĒĢ£ ļČäņĢ╝ņŚÉņä£ ĒÖ£ņÜ®ĒĢĀ ņłś ņ׳ņØä Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢśĻ│Ā ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī ĻĖ░Ļ│äĒĢÖņŖĄņØ┤ ĒÖ£ļ░£Ē׳ ņØæņÜ®ļÉśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņĢäļלņÖĆ Ļ░ÖņØĆ ĒĢ£Ļ│äņĀÉņØä ĻĘ╣ļ│ĄĒĢ┤ņĢ╝ ĒĢ£ļŗż.
4.1 ļŹ░ņØ┤Ēä░ ļČĆņĪ▒
ĻĖ░Ļ│äĒĢÖņŖĄņØä ņØ┤ņÜ®ĒĢ┤ ļ¼╝ņ¦łņØś ĒŖ╣ņä▒ņØä ņĀĢĒÖĢĒĢśĻ▓ī ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļīĆļ¤ēņØś ļŹ░ņØ┤Ēä░ļź╝ ĒĢÖņŖĄņŚÉ ņØ┤ņÜ®ĒĢ┤ņĢ╝ ĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī Ēśäņ×¼Ļ╣īņ¦Ć ĻĖ░Ļ│äĒĢÖņŖĄņØä ņĀüņÜ®ĒĢĀ ļ¦īĒü╝ ņČ®ļČäĒĢ£ ļŹ░ņØ┤Ēä░Ļ░Ć ņĪ┤ņ×¼ĒĢśļŖö ļČäņĢ╝ļŖö ĒĢ£ņĀĢņĀüņØ┤ļŗż. ĒŖ╣Ē׳ Ēæ£ļ®┤ņØś ĒØĪņ░®ņŚÉļäłņ¦ĆĻ░Ć ĒÖ£ņä▒ņØä Ļ▓░ņĀĢĒĢśļŖöļŹ░ ņżæņÜöĒĢ£ ņŚŁĒĢĀņØä ĒĢśļŖö ņ┤ēļ¦ż ļČäņĢ╝ņØś Ļ▓ĮņÜ░, ļ¼╝ņ¦łņØś ņĪ░ņä▒, ļŗżņ¢æĒĢ£ Miller IndexņØś Ēæ£ļ®┤, ĒØĪņ░® ņ×Éļ”¼, ĒØĪņ░®ļ¼╝ņØś ņĪ░ĒĢ® ļō▒ ĻĄēņןĒ׳ ļ¦ÄņØĆ Ļ▓ĮņÜ░ņØś ņłśĻ░Ć ņāØĻĖ░ļŖöļŹ░, ņØ┤ļź╝ ĒĢÖņŖĄĒĢśĻĖ░ņŚÉ ņĀüņĀłĒĢ£ ļŹ░ņØ┤Ēä░ļ▓ĀņØ┤ņŖżĻ░Ć ĒĢ£ņĀĢņĀüņØ┤ļŗż. ņĀ£ĒĢ£ņĀüņØĖ ļŹ░ņØ┤Ēä░ļōżņØä ĒåĄĒĢ┤ ĻĖ░Ļ│äĒĢÖņŖĄņØä ņ¦äĒ¢ēĒĢĀ Ļ▓ĮņÜ░ ĒĢ┤ļŗ╣ ļŹ░ņØ┤Ēä░ņÖĆ ņ£Āņé¼ĒĢ£ Ļ▓ĮņÜ░ļ¦ī ņśłņĖĪņØ┤ ņל ļÉśņ¢┤ ņśłņāü ļ░¢ņØś Ļ▓░Ļ│╝ļź╝ ĻĖ░ļīĆĒĢśĻĖ░ ņ¢┤ļĀĄļŗż. ļö░ļØ╝ņä£ ĻĖ░Ļ│äĒĢÖņŖĄņØä ņāłļĪ£ņÜ┤ ņŚ░ĻĄ¼ ļČäņĢ╝ņŚÉ ņĀüņÜ®ĒĢśļŖöļŹ░ ņ׳ņ¢┤ņä£ ņČ®ļČäĒĢ£ ņ¢æņØś ļŹ░ņØ┤Ēä░ ĒÖĢļ│┤ļŖö ĒĢäņłśņĀüņØ┤ļ»ĆļĪ£, ļ╣ĀļźĖ ņŗ£Ļ░ä ļé┤ņŚÉ ļ¦ÄņØĆ ņ¢æņØś ļŹ░ņØ┤Ēä░ļź╝ ĒÖĢļ│┤ĒĢśļŖö ļ░®ļ▓ĢņØä Ļ░£ļ░£ĒĢśĻ▒░ļéś ĻĖ░ņĪ┤ņØś ļ¬©ļŹĖļōżļ│┤ļŗż Ēø©ņö¼ ņĀüņØĆ ņ¢æņØś ļŹ░ņØ┤Ēä░ļź╝ ņé¼ņÜ®ĒĢ┤ņä£ ņ£Āņé¼ĒĢ£ ņĀĢĒÖĢļÅäļź╝ ļŗ¼ņä▒ĒĢśļŖö ņĀĢĻĄÉĒĢ£ ļ¬©ļŹĖ Ļ░£ļ░£ņØ┤ ņżæņÜöĒĢśļŗż.
4.2 ļ¬©ļŹĖ ĒĢ┤ņäØņØś ņ¢┤ļĀżņøĆ
ĻĖ░Ļ│äĒĢÖņŖĄņŚÉņä£ ņøÉņ×É ĻĄ¼ņĪ░ņŚÉ ļīĆĒĢ£ ņĀüņĀłĒĢ£ ņ×ģļĀź Ēæ£Ēśä ņØĖņ×Éļź╝ ņäĀĒāØĒĢśļŖö Ļ▓āņØĆ ļ¬©ļŹĖņØś ņä▒ļŖźņŚÉ Ēü░ ņśüĒ¢źņØä ļü╝ņ╣£ļŗż. ĒĢśņ¦Ćļ¦ī Ēśäņ×¼Ļ╣īņ¦Ć Ļ░£ļ░£ļÉ£ ļīĆļČĆļČäņØś ĻĖ░Ļ│äĒĢÖņŖĄ ļ¬©ļŹĖņØ┤ Black Box ņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ, ņØ┤ļ¤¼ĒĢ£ ņ×ģļĀź Ēæ£Ēśä ņØĖņ×ÉļōżņØ┤ ņ¢┤ļ¢╗Ļ▓ī ļ¬®Ēæ£Ļ░Æ ņśłņĖĪņŚÉ ņśüĒ¢źņØä ļ»Ėņ╣śļŖöņ¦Ć ņØ┤ĒĢ┤ĒĢśĻĖ░ ņ¢┤ļĀĄļŗż. ņśłļź╝ ļōżņ¢┤ ņØĖĻ│ĄņŗĀĻ▓Įļ¦ØņØś Ļ▓ĮņÜ░, ņ×ģļĀź Ēæ£Ēśä ņØĖņ×ÉņÖĆ ļ¬®Ēæ£Ļ░Æ ņé¼ņØ┤ņŚÉ ņłś ļ¦ÄņØĆ ļģĖļō£ļōżņØ┤ ņĪ┤ņ×¼ĒĢśĻ│Ā ņØ┤ļōżņØĆ ļ¦żņÜ░ ļ│Ąņ×ĪĒĢśĻ▓ī ņŚ░Ļ▓░ļÉśņ¢┤ ņ׳ĻĖ░ ļĢīļ¼ĖņŚÉ ņ£ĀņØśļ»ĖĒĢ£ ļ¼╝ļ”¼ņĀü Ļ┤ĆĻ│äļź╝ ļÅäņČ£ĒĢ┤ļé┤ļŖö Ļ▓āņØĆ ļČłĻ░ĆļŖźĒĢśļŗż. ņĄ£ĻĘ╝ņŚÉļŖö ņØ┤ļ¤¼ĒĢ£ ļ¼ĖņĀ£ļź╝ ĻĘ╣ļ│ĄĒĢśĻ│Āņ×É ņ×ģļĀź Ēæ£Ēśä ņØĖņ×ÉņÖĆ ļ¬®Ēæ£Ļ░Æ ņé¼ņØ┤ņØś ņ¦üĻ░äņĀæņĀüņØĖ Ļ┤ĆĻ│äļź╝ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŖö ņåīņ£ä Grey Box ļśÉļŖö Glass Box ļ¬©ļŹĖļōżņØ┤ Ļ░£ļ░£ļÉśĻ│Ā ņ׳ņ¦Ćļ¦ī, ņ×ģļĀź Ēæ£Ēśä ņØĖņ×ÉņÖĆ ļ¬®Ēæ£Ļ░Æ ņé¼ņØ┤ņØś ņāüĻ┤ĆĻ┤ĆĻ│ä ļČäņäØņŚÉ ĻĘĖņ╣śĻ│Ā ņ׳ļŗż. ņČöĒøä ņäżļ¬ģĻ░ĆļŖźĒĢ£ ĻĖ░Ļ│äĒĢÖņŖĄ ļ¬©ļŹĖņØś Ļ░£ļ░£ņØ┤ ņŗĀņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ ļ¦żņÜ░ ņżæņÜöĒĢ£ ņŚŁĒĢĀņØä ĒĢĀ Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢ£ļŗż.
5. Ļ▓░ļĪĀ
ņ╗┤Ēō©Ēä░ ĻĖ░ņłĀĻ│╝ ņĢīĻ│Āļ”¼ņ”śņØś ļ░£ņĀäņØĆ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņØ┤ņÜ®ĒĢ┤ ņāłļĪ£ņÜ┤ ņ┤ēļ¦żļź╝ Ļ░£ļ░£ĒĢśļŖö ņŚ░ĻĄ¼ ļČäņĢ╝ņŚÉ Ēü░ ņśüĒ¢źņØä ļü╝ņ╣śĻ│Ā ņ׳ļŗż. ņłś ļ¦ÄņØĆ ņŗ£Ē¢ēņ░®ņśżļź╝ ļÅÖļ░śĒĢśļŖö ĻĖ░ņĪ┤ņØś ņŗżĒŚś ņżæņŗ¼ ņŚ░ĻĄ¼ņŚÉņä£ ļ▓Śņ¢┤ļéś, ļŹö ļäōņØĆ ĒÖöĒĢÖĻ│ĄĻ░äņŚÉ ņĪ┤ņ×¼ĒĢśļŖö ņ┤ēļ¦żļōżņØä Ļ░Ćņāüņ£╝ļĪ£ ņŗĀņåŹĒĢśĻ▓ī ĒāÉņāēĒĢĀ ņłś ņ׳Ļ▓ī ļÉśņŚłļŗż. ĒŖ╣Ē׳, DFT ĻĖ░ļ░śņØś Ļ│äņé░ĒÖöĒĢÖ ņŚ░ĻĄ¼ļŖö ņ¦Ćļé£ 20ļģäĻ░ä ņŗżņĀ£ ņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ ĒÖ£ņÜ®ļÉśņ¢┤ ļŗżņ¢æĒĢ£ ņÜ░ņłś ņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ ĻĖ░ņŚ¼ĒĢśņśĆļŗż. ĒĢśņ¦Ćļ¦ī ļŗżļŻ©Ļ│Āņ×É ĒĢśļŖö ļ¼╝ņ¦łņØś ņłśĻ░Ć ļ¦ÄņĢäņ¦Ćļ®┤ņä£ DFT Ļ│äņé░ ņŗ£Ļ░äņØ┤ ņ┤ēļ¦ż ņäżĻ│äņŚÉ ņןņĢĀļ¼╝ņØ┤ ļÉśņ¢┤, ĻĖ░Ļ│äĒĢÖņŖĄņØä ņØ┤ņÜ®ĒĢ┤ ĒĢäņÜöĒĢ£ DFT Ļ│äņé░ ņłśļź╝ ņżäņØ┤Ļ│Āņ×É ĒĢśļŖö ņĀæĻĘ╝ļ▓ĢņØ┤ Ļ┤Ćņŗ¼ņØä ļ░øĻ│Ā ņ׳ļŗż. ĻĖ░Ļ│äĒĢÖņŖĄņØä ĒåĄĒĢ£ ņ┤ēļ¦ż ņŚ░ĻĄ¼ļŖö ļČäņĢ╝ņŚÉ ļö░ļźĖ ļŹ░ņØ┤Ēä░ ņ¢æņØś ĒÄĖņ░© ļ░Å ļČĆņĪ▒, ļ¬©ļŹĖ ĒĢ┤ņäØņØś ņ¢┤ļĀżņøĆ ļō▒ ĒĢ┤Ļ▓░ĒĢ┤ņĢ╝ ĒĢĀ ņłÖņĀ£Ļ░Ć ņ׳ņ¦Ćļ¦ī, ņĄ£ĻĘ╝ņŚÉļŖö ņØ┤ļź╝ ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢ┤ Ļ░ĢĒÖöĒĢÖņŖĄ, ļŖźļÅÖĒĢÖņŖĄ, ņäżļ¬ģĻ░ĆļŖźĒĢ£ ļ¬©ļŹĖ ļō▒ņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£Ē׳ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż. ņ┤ēļ¦ż Ļ░£ļ░£ņŚÉ ņ׳ņ¢┤ Ļ│äņé░ĒÖöĒĢÖĻ│╝ ĻĖ░Ļ│äĒĢÖņŖĄņØś ĒÖ£ņÜ®ņØ┤ ļ╣Āļź┤Ļ▓ī ļŖśņ¢┤ļéśļŖö ļ¦īĒü╝, ņČöĒøä ļČäņĢ╝ļź╝ ņäĀļÅäĒĢĀ ļ░®ļ▓ĢļĪĀņ£╝ļĪ£ ņ×Éļ”¼ļ¦żĻ╣ĆĒĢĀ Ļ▓āņ£╝ļĪ£ ĻĖ░ļīĆĒĢ£ļŗż.